概述
B+Tree是一种数据结构,也是Mysql中Innodb数据库引擎中的主要使用索引。在2019年的时候,在自己从头到尾实现了一遍红黑树之后,突然想实现一遍B+Tree。在加上2018年的时候看了一本书《高性能Mysql》,这本书对我后面优化sql的思路有挺大的影响的。里面有从源头解释优化,但是我只挑了重点看。
我一直认为,要解析某个事物,首先得知道,创造这个事物的人是怎么想的。sql优化的主要手段是利用索引查找,那为什么用上索引就这么高效?
总之,我去自己实现了一遍B+Tree,就是为这么个目的。
索引种类
索引本质是一种数据结构,可以帮助数据库快速查找的数据结构,即减少查找的时间复杂度。
哈希索引
顾名思义,是一种哈希表结构的索引。想理解它,只需要理解好HashMap的结构功能就好了。
①HashMap存的是key-value键值对,即等值查找。所以哈希索引的特点是适合于等值查找的场景。
②在我以前实现HashMap和使用HashMap时知道,HashMap存储数据由于hash算法,导致它的数据存储不是顺序的,所以HashMap无法提供按key的范围直接取数据。那么就可以知道哈希索引的缺点是无法范围查找。
二叉树索引
顾名思义,是一种二叉树结构的索引。所以需要去理解二叉树这种数据结构即可。
①二叉树特点是 左节点<父节点<右节点,可以范围查找;
②一颗平衡的二叉树,查找的时间复杂度相当于折半查找;
③一颗极度不平衡的二叉树会退化成一条链表,查找的时间复杂度最大;
④在数据越来越多的情况下,二叉树的深度势必会越来越深,查找也会越来越困难。
二叉树索引的高度越来高,数据库只能将其压缩存储在磁盘中,代表着每次使用索引的时候,需要从磁盘取出,增加了磁盘IO拖慢了速度。
综上,虽然说二叉树索引解决了哈希索引无法范围查找的问题。平均的等值查找比哈希索引慢了许多,甚至在极端的情况还不如用哈希索引。
BTree索引
BTree,全名叫多路平衡树。
与普通二叉树的区别是:
①一个树节点可以存多个数据
与红黑树的区别是:
①BTree的平衡不是通过旋转变色来实现,而是通过向下分裂来实现。
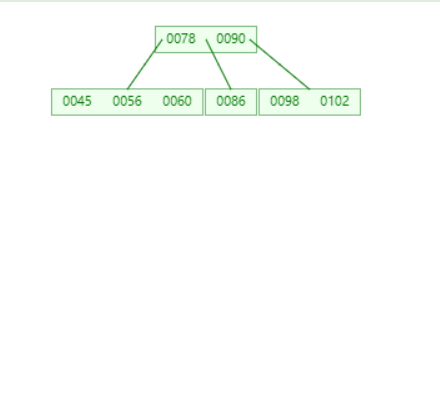
相对于二叉树索引:
①由于一个树节点可以存储多个数据,有效的缩小了树的深度。
②通过向下分裂,保持平衡,避免退化成一条链表
在Mysql数据库中,BTree索引一般是MyISAM数据引擎在使用。并且,为节省空间,MyISAM数据引擎对索引的值进行压缩存储。比如有个数据为 string,第二个数据strgda在索引中会存储为 3,gda,以达到节约空间的目的。
B + Tree索引
B+Tree也是多路平衡树。
它和BTree的区别是:
①在结构上,B+Tree的所有叶子节点是一条链表,而BTree的叶子节点就是单纯的叶子节点
②在数据存储上,B+Tree的叶子节点链表存储着所有的节点数据,从小到大排序
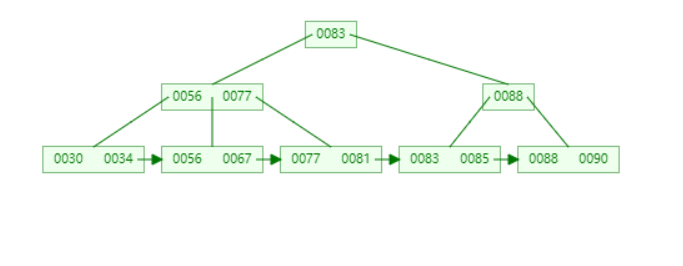
为什么B+Tree要将所有数据在叶子节点都有一份,并且还要形成一条有序链表?
答:
当时我在研究实现B+Tree的时候一直有这么一个疑问。
后面某一时刻突然想通了,在sql查询中,存在一种情况:
· 当order by count asc时,且存在一个count字段的索引。
· 如果索引是BTree,那么代表mysql要从小到大扫描整棵索引树,直接扫描树需要用到中序遍历,中-左-中-右。每个节点被遍历的次数>=1,每次还要存储一个存储一个栈结构维护输出顺序。这明显就存在性能瓶颈了
· 如果索引是B+Tree,问题就简单了许多。①所有数据都在叶子节点上 ②叶子节点形成了一条有序链表。so,ㄟ( ▔, ▔ )ㄏ直接遍历叶子节点链表就行了,每个节点只会被访问一次,也不需要一个栈维护顺序,时间复杂度直接O(n)。
实现过程
B+Tree 基本特征
要实现一个数据结构,首先得明白它是个什么,结构有基本特点,有哪些性质。
①多路节点
②一个树节点中,有多个数据,数据个数大于等于N时,分裂成三部分:左、中、右,这三部分变成三个树节点,中间树节点成为左右两部分的父节点。
③所有叶子节点形成一条有序链表
④所有数据都在叶子节点上
大体结构设计
①一个树节点看作一个类;
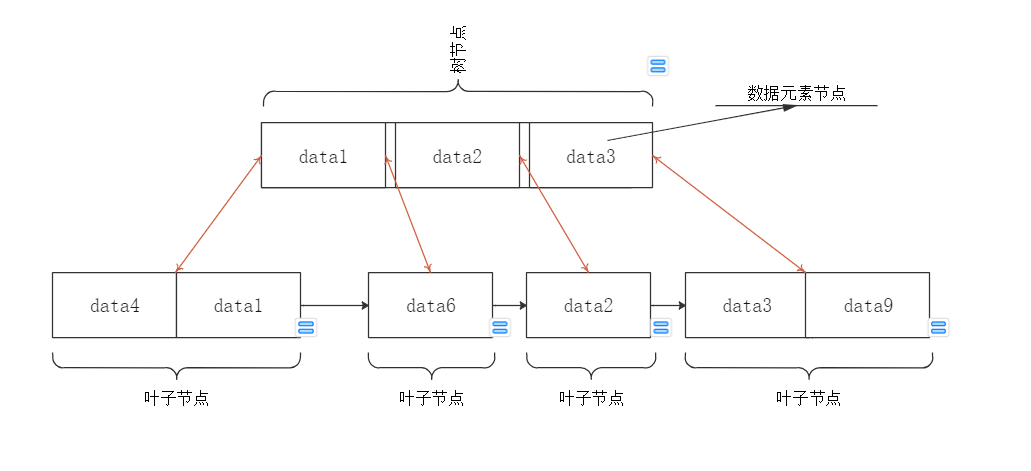
②树节点类里面有多个数据元素节点,数据元素看作一个类;
③树节点类中有父节点指针
④数据元素节点中有左右子树节点指针。我设计的是同一个树节点内,左边第一个元素节点左右可能都有树节点,其他元素节点只有右边有子树节点
⑤叶子节点中维护了一个前后叶子节点的指针,从而形成一条链表
定义类
①首先,B+Tree是有序的,存的数据类型是不确定的。👉所以需要一个比较器Comparable/Comparator,为了方便我选择了Comparable。还需要一个泛型,但这个泛型具体的类型必须得实现了Comparable接口,即该泛型有上限,方便比较。
②B+Tree,得持有一个整棵树的一个入口,即Root节点;一个链表的入口,即head节点。
③B+Tree的结构特点,决定了它需要一些内部类。树节点内部类,树节点里面单个数据类。
④BTree需要分裂平衡,触发条件是,当一个树节点的数据个数大于等于N时,向上分裂。所以需要一个全局变量N。
public class BTree <T extends Comparable<T>> {
private int line=3;//每个节点数据个数
private Node root;
private Node head;//叶子节点链表头
/**
* 树节点
* @author Administrator
*
*/
private class Node<T>{
//维护叶子节节点链表顺序使用
private Node pre;
//父节点
private Node parnet;
//树节点中元素节点集合
private List<Element<T>> eles;
//维护叶子节节点链表顺序使用
private Node next;
public Node(){
eles=new LinkedList<>();
}
public Node(Element ele){
this();
eles.add(ele);
}
public Node(List<Element<T>> eles){
this.eles=new LinkedList<>();
this.eles.addAll(eles);
}
@Override
public String toString() {
if(eles==null){
return null;
}
StringBuilder sb=new StringBuilder();
for(Element e:eles){
sb.append(e.data).append(",");
}
return "Node [eles=" + sb.toString() + "]";
}
}
/**
* 单个元素节点
* @param <T>
*/
private class Element<T>{
private T data;
//元素节点的左子树节点
private Node left;
//元素节点的右子树节点
private Node right;
public Element(T data){
this.data=data;
}
@Override
public String toString() {
return "Element [data=" + data + ", left=" + left + ", right=" + right + "]";
}
}
}
构造方法
肯定是要传递一个参数进来的,几路平衡树,即一个树节点有几个元素。关系到分裂平衡。
private int line=3;//每个树节点能包含元素节点的最大个数
public BTree(int line){
this.line=line;
}
添加数据
可视化过程
以四路平衡树为例
1.首先在数据个数小于四时,肯定就一个root节点

2.当root节点的数据元素个数达到4个时,触发分裂
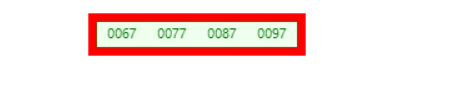
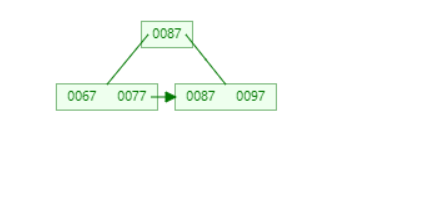
3.分裂成三部分,4/2=2,以中间下标为界线。所以[67,77]、[87]、[87,97]。问题来了,为什么第三部分是[87,97],因为所有数据都要在叶子节点中找得到。
代码层面实现
B+Tree添加数据过程:
①从root节点开始比较查找,依次比较根节点中所有数据元素。没找到合适的位置,继续往下一个节点找。
②当定位到某个树节点,在该节点中找到插入位置,将数据插入树节点。
③判断该树节点是否大于等于N。
a. 是,则将该树节点分裂成三个节点,形成一棵小子树。
b. 否,直接插入。
关于B+Tree的分裂平衡,详细解析往下看。
add(T t)方法
public boolean add(T t){
//若还root为null,说明该树还没有任何节点
if(root==null){
root=new Node(new Element<T>(t));
head=root;
return true;
}
BTree<T>.Element<T> ele = new Element<>(t);
Node<T> currentNode=root;
A:while(true){
//获取当前访问树节点存储的数据列表
List<Element<T>> eles = currentNode.eles;
/**
*查找要添加元素ele,在当前树节点currentNode数据元素中第一个大于ele的元素节点的
*下标
*/
int i=findSetPositInEles(ele, currentNode);
Node nextNode=null;
/**
* i>0,代表i处元素节点a刚好大于要插入节点b,所以b要从a的左边找。由前面我对于
* B+Tree的结构设计可知,除了第一个元素节点外,其他只有右子树节点。所以a的左边即
* a前面一个节点的右子树节点
*/
if(i>0){
nextNode = eles.get(i-1).right;
}else{//i<=0,说明要插入节点比该树节点所有元素节点都要小
//节点最左边往下找
nextNode = eles.get(0).left;
}
if(nextNode==null){
eles.add(i, ele);
//判断是否需要分裂
if(eles.size()==line){
//分裂平衡方法
spiltNode(currentNode);
}
break A;
}
currentNode=nextNode;
}
return true;
}
findSetPositInEles
/**
* 寻找新ele应该插入节点elements集合中的位置<br>
* ps:可以用二分法性能更好
* @param ele
* @param node
* @return
*/
public int findSetPositInEles(Element<T> ele,Node node){
List<Element<T>> eles = node.eles;
int i=0;
for(;i<eles.size();i++){
//当找到第一个大于等于ele的元素节点,返回对应下标
if(ele.data.compareTo(eles.get(i).data)<=0){
return i;
}
}
return i;
}
spiltNode(Node node) 分裂平衡
node分裂过程(针对的是一个树节点的分裂):
1.根据元素节点个数len计算中间下标mid
2.判断是否叶子节点
2.1 是叶子节点,拆分成三个节点:
[0,mid-1]→lnode, [mid]→mnode, [mid,len-1]→rnode
2.2 非叶子节点,拆分成三个节点:
[0,mid-1]→lnode, [mid]→mnode, [mid-1,len-1]→rnode
3.若node原来有父节点pnode,则mnode整合到pnode中;若node没有父节点,则mnode直接变成一个父节点pnode
4.lnode、rnode成为pnode子节点
5.若node原来是叶子节点,则需要维护叶子节点形成的链表,node部分替换成 lnode→rnode
6.判断pnode是否需要分裂
6.1 需要,到第1步
6.2 不需要,结束
/**
* 分裂平衡
*/
@SuppressWarnings("unchecked")
private void spiltNode(BTree<T>.Node<T> node){
int mid=line/2;
A:while(true){
//是否叶子节点
boolean isLeafNode=node.next!=null||node.pre!=null||head==node;
List<Element<T>> eles = node.eles;
List<BTree<T>.Element<T>> leftEles = eles.subList(0, mid);
//叶子节点一分为二,并生成一个和中间元素节点相同值的元素节点,向上推到父节点中;非叶子节点一分为三,正中间的元素节点向上推到父节点中
List<BTree<T>.Element<T>> rightEles = eles.subList(isLeafNode?mid:mid+1,eles.size());
//分裂出来的左节点
BTree<T>.Node<T> leftNode=new Node<T>(leftEles);
//分裂出来的右节点
BTree<T>.Node<T> rightNode=new Node<T>(rightEles);
//树节点的中间元素节点
BTree<T>.Element<T> spiltEle = eles.get(mid);
BTree<T>.Node<T> parnet = node.parnet;
/**
* 更新叶子节点链表<br>
* <B>该链表是一个双向链表
*/
//若原来分裂的节点是叶子节点需要更新
if(isLeafNode){
//更新叶子节点链表
if(node.pre!=null){
node.pre.next=leftNode;
}else{
head=leftNode;
}
if(node.next!=null){
node.next.pre=rightNode;
}
leftNode.pre=node.pre;
leftNode.next=rightNode;
rightNode.pre=leftNode;
rightNode.next=node.next;
//叶子节点分裂之后,要包含分裂出去的元素,即使值一样,但对象并不一样
// rightEles.set(0, new Element<T>(spiltEle.data)); 隐患,由于rightNode中的eles在内存指向的集合和rightEles不是同一个了,这么并没改变rightNode
rightNode.eles.set(0, new Element<T>(spiltEle.data));
}
/**
* 分裂
*/
//维护下一层的关系
//非叶子节点,分裂出去的element的右节点由剩下右半部分的继承
if(!isLeafNode){
rightNode.eles.get(0).left=spiltEle.right;
//分裂之后对于原node节点的子节点来说,它们的父节点对象也产生了变化
rightNode.eles.get(0).left.parnet=rightNode;
List<Element<T>> foreachList=leftNode.eles;
boolean f=false;
int i=0;
B:while(true){
Element<T> temp=foreachList.get(i);
//第一个元素特殊可能左右都有
if(i==0){
temp.left.parnet=!f?leftNode:rightNode;
if(temp.right!=null){
temp.right.parnet=!f?leftNode:rightNode;
}
}else{
temp.right.parnet=!f?leftNode:rightNode;
}
i++;
if(!f&&i==foreachList.size()){
foreachList=rightNode.eles;
i=0;f=true;
}else if(f&&i==foreachList.size()){
break B;
}
}
}
//维护上一层的关系
if(parnet==null){
//根节点的分裂
spiltEle.left=leftNode;
spiltEle.right=rightNode;
Node<T> newNode=new Node<>(spiltEle);
leftNode.parnet=newNode;
rightNode.parnet=newNode;
root=newNode;
return ;
}else{
//将spiltEle插入父节点
List<Element<T>> pEles = parnet.eles;
int positInEles = findSetPositInEles(spiltEle, parnet);
pEles.add(positInEles, spiltEle);
if(positInEles==0){
pEles.get(0).left=leftNode;
//清空原0位元素的左节点
pEles.get(1).left=null;
}else{
pEles.get(positInEles-1).right=leftNode;
}
pEles.get(positInEles).right=rightNode;
leftNode.parnet=parnet;
rightNode.parnet=parnet;
//继续判断parent是否需要分裂
if(pEles.size()>=line){
node=parnet;
}else{
return ;
}
}
}
}