2002.05.29 力扣 - 数组 - 11 盛最多水的容器

题目

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点(i, ai) 。

在坐标内画 n 条垂直线，垂直线i的两个端点分别为(i, ai) 和 (i, 0)。

找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且n的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。

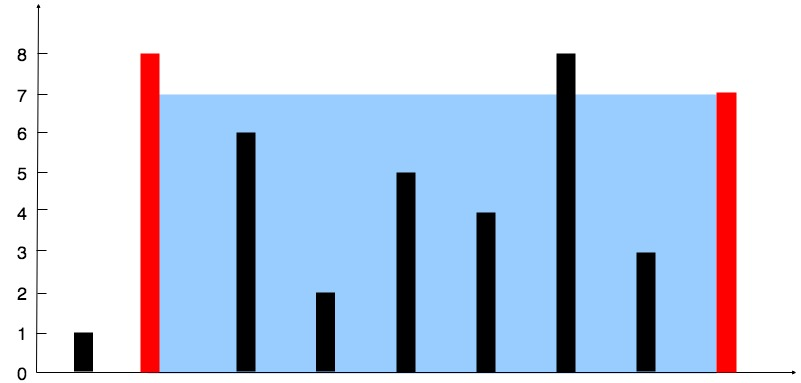
在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例

输入：[1,8,6,2,5,4,8,3,7]

输出：49

思路

猜测是二维数组或者双指针的考察点，在纸上推演了双指针，但无从下手，所以还是直接学习官方教程了。

代码

func maxArea(height []int) int {
	cnt := len(height)
	if cnt < 2 {
		return 0
	}

	maxArea := 0
	left := 0
	right := cnt - 1
	for left < right {
		area := (right - left) * min(height[left], height[right])
		maxArea = max(maxArea, area)
		if height[left] <= height[right] {
			left++
			continue
		}
		right--
	}
	return maxArea
}

func min(a, b int) int {
	if a <= b {
		return a
	}
	return b
}

func max(a, b int) int {
	if a <= b {
		return b
	}
	return a
}

分析

时间复杂度：O(n)

空间复杂度：O(1)