强化学习总结02 马尔可夫决策过程

白话Python
3,015 阅读4分钟

马尔科夫性 - 马尔可夫过程 - 马尔可夫奖励过程 - 马尔可夫决策过程

概述

马尔可夫决策过程（Markov Decision Processes, MDPs）是对强化学习问题的数学描述。

  • 要求环境是全观测的。

马尔可夫性

“ 只要知道现在，将来和过去是条件独立的，可以抛去过去所有的信息。”

定义：如果在t时刻的状态S_t满足下式，则这个状态被称为马尔科夫状态，即该状态满足马尔科夫性

P[S_{t+1}|S_{t}] = P[S_{t+1}|S_1, ..., S_t]

注：

  • 状态S_t包含了所有历史相关信息，即之前的信息都可以在该状态上体现出来（S_t可以代替所有之前的状态）
  • 所以要求环境是全观测的，(如果是部分观测的话，状态信息有缺失)。
  • 是否满足马尔可夫性与状态的定义息息相关

例子：

  • 下棋
  • 俄罗斯方块

有了马尔可夫状态之后：

  • 可以定义状态转移矩阵
  • 忽略时间的影响，只关心当前时刻

注： 状态是否满足马尔可夫性，与状态的定义息息相关。

状态转移矩阵

状态转移概率

状态转移概率指从一个马尔可夫状态 s 跳转到后继状态 (successor state) s′ 的概率。是关于当前状态的条件概率分布。

\mathcal{P} _ {ss^{'}} = {P} [S_{t+1} = s^{'} | S_t = s]

状态转移矩阵

若状态是离散的（有限个）：

  • 所有的状态组成行
  • 所有后继状态组成列，

得到状态转移矩阵

\mathcal{P} = \begin{bmatrix} \mathcal{P} _ {11} & ... & \mathcal{P} _ {1n} \\ ... & ... & ... \\ \mathcal{P} _ {n1} & ... & \mathcal{P} _ {nn} \\ \end{bmatrix}
  • n为状态个数
  • 每行元素相加为1

状态转移函数

若**状态数量过多，或者无穷大（连续状态）**的，适合用本节最上式的函数形式表示。

\mathcal{P} _ {ss^{'}} = {P} [S_{t+1} = s^{'} | S_t = s]
  • 此时，\int_{s'}\mathcal{P}(s'|s)=1

马尔可夫过程

定义

一个马尔可夫过程 (Markov process, MP) 是一个无记忆的随机过程，即一些马尔可夫状态的序列。

马尔可夫过程可由一个二元组来定义 < S,\mathcal{P} >

  • S：代表状态集合
  • \mathcal{P}：代表状态转移矩阵

通常假设\mathcal{P}是存在且稳定的 当\mathcal{P}不稳定时，采用在线学习、快速学习等方法

马尔可夫过程的例子

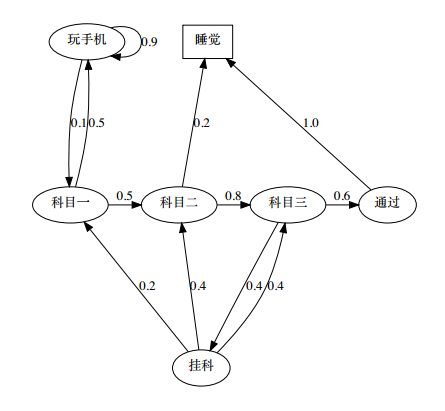
  • 马尔可夫过程中的终止状态有2种：
    • 时间终止
    • 状态终止

片段（Episode）

定义： 强化学习中，从初始状态 S_1 到终止状态 S_T 的序列过程。

S_1, S_2, ..., S_T

马尔可夫奖励过程

定义

在马尔可夫过程的基础上，在转移关系中赋予不同的奖励值，即得到马尔可夫奖励过程。

马尔可夫奖励 (Markov Reward Process, MRP) 过程由一个四元组组成 ⟨S, \mathcal{P}, \mathcal{R}, γ⟩

  • S：状态集合
  • \mathcal{P}：状态转移矩阵
  • \mathcal{R}：奖励函数， \mathcal{R}(s) 描述了在状态 s 的奖励，\mathcal{R}(s) = E [\mathcal{R}_{t+1}|S_t = s]
  • γ：衰减因子

回报值

  • 奖励值：对一个状态的评价
  • 回报值：对一个片段的评价

回报值（return G_t）是从时间t处开始的累积衰减奖励

G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ...

MRPs中的值函数

为什么要值函数？ 回报值是一个片段的结果，存在很大的样本偏差 回报值的角标是 t，值函数关注的是状态 s

一个 MRP 的值函数如下定义

v(s) = {E}[G_t|S_t = s]

这里的值函数针对的是状态 s，所以称为状态值函数，又称 V 函数

MRPs中的贝尔曼方程（重点）

\begin{aligned}v(s)&={E}[G_t|S_t=s] \\ &={E}[ R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... | S_t=s] \\ &={E}[ R_{t+1} + \gamma G_{t+1} | S_t=s ] \\ &={E}[ R_{t+1} + \gamma v(S_{t+1}) | S_t=s ]\end{aligned}

当前状态的值函数包括两部分：

  • 第一项：瞬时奖励 R_{t+1}
  • 第二项：后继状态的值函数乘衰减系数 \gamma v(S_{t+1})

由于后继状态可能有多个，因此如果已知转移矩阵 P，那么

\begin{aligned} v(s) &= {E} [R_{t+1} + γv(S_{t+1}) | S_t = s] \\ &= {E} [R_{t+1} | S_t = s] + γ {E}[v(S_{t+1})|S_t = s] \\ &= \mathcal{R}(s) + γ ∑\mathcal{P}_{ss^′}v(s^′)\end{aligned}

矩阵-向量形式为：

v = \mathcal{R} + \gamma \mathcal{P} v

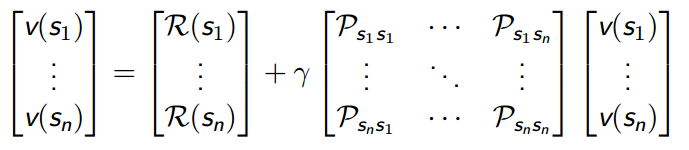
本质上是一个线性方程，可以直接解：

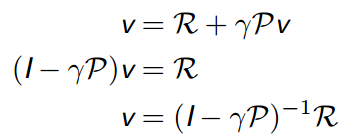
直接求解只适用于小型MRPs：

  • 计算复杂度O(n^3)
  • 要求已知 \mathcal{P}

马尔可夫决策过程

MP 和 MRP 中，我们都是作为观察者，去观察其中的状态转移现象，去计算回报值。对于一个 RL 问题，我们更希望去改变状态转移的流程，去最大化回报值。因此，在 MRP 中引入决策，得到马尔可夫决策过程（Markov Decision Processes, MDPs）

定义

一个马尔可夫决策过程 (MDPs) 由一个五元组构成 ⟨S, \mathcal{A}, \mathcal{P}, \mathcal{R}, γ⟩

  • \mathcal{A} ： 动作的集合
  • \mathcal{P} ： 状态转移矩阵
\mathcal{P}_{ss^{'}}^{a} = {P}[ S_{t+1}=s' | S_t=s, A_{t}=a]
  • \mathcal{R}(s,a)：奖励函数， 表示在状态s做动作a的奖励。\mathcal{R}(s, a) = E [\mathcal{R}_{t+1}|S_t = s, A_{t}=a]

策略

在 MDPs 中，一个策略 (Policy)π 是在给定状态下的动作的概率分布

\pi(a | s) = {P}[ A_t = a | S_t = s ]

  • 策略是时间稳定的，只与s有关，与时间t无关
  • 是RL问题的终极目标
  • 如果分布是 one-hot 的，那么为确定性策略，否则为随机策略

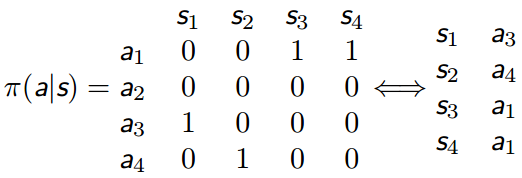
MDPs与MRPs之间的关系

如果MDP问题给定策略\pi，则会退化成MRP问题。

MDPs中的值函数

  1. 状态值函数（V函数）

    • 定义：从状态s开始，使用策略\pi得到的期望回报值
    v_{\pi}(s) = {E}_\pi[G_t|S_t = s]

  2. 状态动作值函数（Q函数）

    • 定义：MDPs 中的状态动作值函数是从状态 s 开始，执行动作 a， 然后使用策略 π 得到的期望回报值

      动作a不一定来自于策略 \pi，实际上是做完动作 a之后，才遵循策略 \pi 进行动作选择

    q_{\pi}(s, a) = {E}_\pi[ G_t | S_t = s, A_t = a ]

贝尔曼期望方程

和 MRP 相似， MDPs 中的值函数也能分解成瞬时奖励和后继状态的值函数两部分

v_ \pi(s)={E}_ \pi [ R_{t+1} + \gamma v_ \pi(S_{t+1}) | S_t=s ]
q_ \pi(s,a)={E}_ \pi [ R_{t+1} + \gamma q_ \pi(S_{t+1}, A_{t+1}) | S_t=s, A_t=a]
avatar
文章
阅读
粉丝