1 哈夫曼树
1.1 介绍
在学习编程的过程中,一定遇到过类似以下的情景:记录一个班的同学的成绩,通过分数输出评价。
if (score < 60) {
result = "不及格";
} else if (score < 70) {
result = "及格";
} else if (score < 80) {
result = "中等";
} else if (score < 90) {
result = "良好";
} else {
result = "优秀";
}
假如根据统计结果或往年数据,得出每个阶段的比例如下所示:
| 分数 | 0 ~ 59 | 60 ~ 69 | 70 ~ 79 | 80 ~ 89 | 90 ~ 100 |
|---|---|---|---|---|---|
| 比例 | 5% | 15 % | 40% | 30% | 10% |
可以看到 70+ 和 80+ 的人数占大多数。在这种情况下,对于以上代码,前两层 if 命中率低,产生大量的多余判断。一般情况下没有问题,但是如果数据量很大,并且每层的 if 判断比较耗时,那么就需要对判断的流程进行结构的优化。
我们将每个 if 判断视为一个结点,整个流程将变成一个二叉树结构:
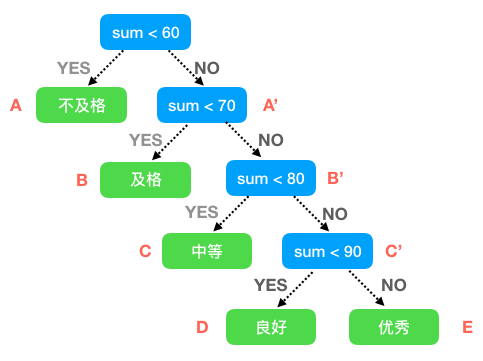
在之前树的章节中介绍了树的深度:从根开始定义起,根为第1层,根的子结点为第2层,以此类推。这里我们以路径的角度去分析结点的深度。每个结点到根节点中间存在的树枝(线段)数称为该结点的路径长度,树的路径⻓度就是从树根到每一个结点的路径长度之和。
图中个结点的路径长度如下:
| 分数 | A | A' | B | B' | C | C' | D | E |
|---|---|---|---|---|---|---|---|---|
| 路径长度 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
整个树的路径长度为:1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 = 20。
在本例中路径长度即代表了 if 判断的次数。D 的路径长度为 4 代表需要 4 次 判断才能得到结果 D。
结合之前的统计数据,我们将每种可能的结果(即每个叶子节点)的路径长度,乘上其发生的概率(即权值),最后加到一起,就得到了树的带权路径长度,简称 WPL (Weighted Path Length of Tree)。
计算树的路径长度时包含了所有的节点的路径长度。(可以理解根节点的路径为0)
计算树的 WPL 时只计算叶子节点的带权长度。
| 结点 | A | B | C | D | E |
|---|---|---|---|---|---|
| 路径长度 | 1 | 2 | 3 | 4 | 4 |
| 权值 | 5 | 15 | 40 | 30 | 10 |
整个树的 WPL 为:1 x 5 + 2 x 15 + 3 x 40 + 4 x 30 + 4 x 10 = 315。
这个数表示了在上述概率下,每种结果的平均路径长度,即判断一次成绩时 if 执行的平均次数,为 3.15 次。直观上来讲 4 个 if 平均执行 3.15 次确实不小。 如果依照概率从大到小来进行判断,依次判断 D、C、B、E、A ,也可以容易猜出 WPL 必然会小于 3.15。
除此之外,我们可以通过构建哈夫曼树,来进行最短路径的求解,得到如下最短路径树:
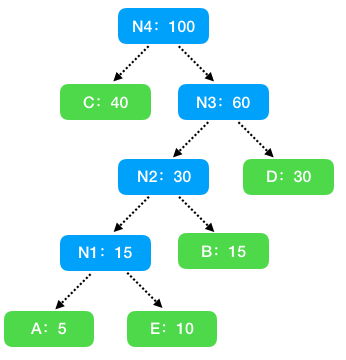
| 结点 | A | B | C | D | E |
|---|---|---|---|---|---|
| 路径长度 | 4 | 3 | 1 | 2 | 4 |
| 权值 | 5 | 15 | 40 | 30 | 10 |
整个树的 WPL 为:4 x 5 + 3 x 15 + 1 x 40 + 2 x 30 + 4 x 10 = 205。
相比于之前的 315 ,可以理解为 if 的平均执行次数从 3.15 次降低为 2.05 次,有明显的降低。
那么如何构建哈夫曼树呢?下面将介绍什么是哈夫曼树以及哈夫曼编码的原理。
1.2 哈夫曼树介绍
哈夫曼树:给定 n 个权值作为 n 个叶子结点,构造一棵二叉树,若该树的带权路径长度(WPL)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree,或称霍夫曼树)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
哈夫曼编码:在计算机中,每个字符都是通过二进制进行编码。我们把使用相同长度编码的方式称为定长编码。比如一个字符串 "Hello world!'' 需要 12 个字节即 96 个二进制位来存储。但实际中每个字符出现的概率并不相同,比如字母 a、e、i、o、u 出现的概率可能会高,字母 x、z 出现的概率可能很低。哈夫曼编码就是一种基于概率实现的一种变长编码方式。出现次数较多的字符其编码长度就相应地小,反之其编码长度就相应的长。
哈夫曼编码是压缩界的始祖,虽然如今有更优秀的压缩方式,但其思想依旧影响着现在。哈夫曼编码有着广泛的应用,例如在
jpeg文件中,就应用了哈夫曼编码来实现最后一步的压缩;在数字电视大力发展的今天,哈夫曼编码成为了视频信号的主要压缩方式。应当说,哈夫曼编码出现,结束了熵编码不能实现最短编码的历史,也使哈夫曼编码成为一种非常重要的无损编码。(度娘)
1.3 哈夫曼树的构建

如图所示的场景,我们使用三个二进制来对英文字母进行编码。文字包含 n 个字符则需要发送 3n 个二进制数据。
假设通过统计概率得知,每个字母的出现概率如下所示:
| 字符 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 概率 | 27% | 8% | 15% | 15% | 30% | 5% |
则我们可以通过构建哈夫曼树来进行变长编码。
哈夫曼树的构建步骤:
- 取出集合中权值最小的两个结点,构建一颗二叉树,并从集合中移除这两个结点。
- 二叉树的根结点将视为一个新的结点,加入到集合中,其权值为两个子结点的权值之和。
- 重复步骤 1,直到集合中无结点。
其中规定:
- 权值小的作为左子树,权值大的作为右子树。(相等时左右无影响)
- 编码时左子树为 0,右子树为 1。
根据步骤开始构建哈夫曼树:
- 取出权值最小的两个结点 B:8 和 F:5 构建二叉树。且权值小的作为左子树,大的作为右子树。
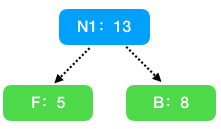

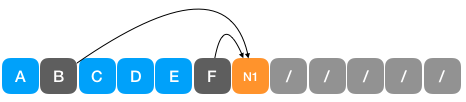
此时集合中的结点情况如上所示,N1 为新加入的节点,其权值为。
- 从新的集合中取出最小的两个节点 N1:13 和 C:15 构建二叉树。
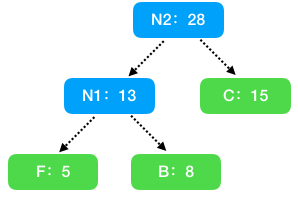

- 从集合中取出最小的两个节点 A1:13 和 C:15 构建二叉树,因为 N2 比这两个节点都大,不参与该步骤的操作,所以 A 和 D 将构建新的子树。
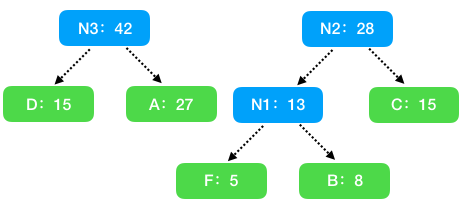
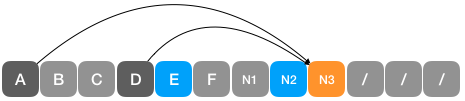
- 从集合中取出最小的两个节点 N2:28 和 E:30 构建二叉树。
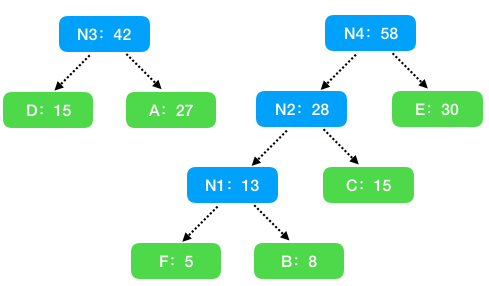
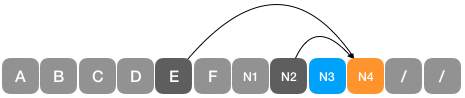
- 从集合中剩余的两个节点N3:42 和 N4: 58 完成哈夫曼树的构建。
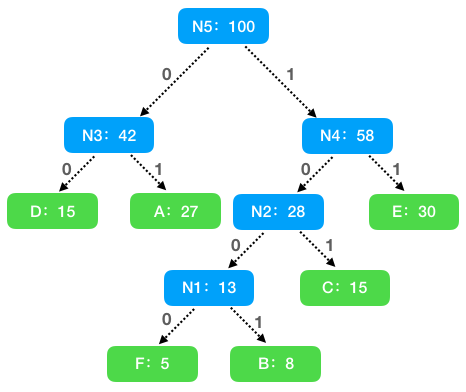

通过构建完成的哈夫曼树,规定左子树编码为 0,右子树编码为 1,则得到新的编码值:
率得知,每个字母的出现概率如下所示:
| 字符 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 概率 | 27% | 8% | 15% | 15% | 30% | 5% |
| 原编码 | 000 | 001 | 010 | 011 | 100 | 101 |
| 哈夫曼编码 | 01 | 1001 | 101 | 00 | 11 | 1000 |
根据新的编码值,发送如下信息:BADCADFEED (A:2 B:1 C:1 D:3 E:2 F:1)
原编码二进制:001 000 011 010 000 011 101 100 100 011 (共30个字符)
新编码二进制:1001 01 00 101 01 00 1001 11 11 00 (共25个字符)
可以清晰地看到在该概率下,哈夫曼编码有效地对数据进行了压缩。
2 代码实现
2.1 结构定义
/// 哈夫曼树节点
typedef struct {
int weight; // 权值
int flag; // 标志位
int parent; // 父结点索引
int lch, rch; // 左右子结点索引
} HaffmanNode;
// 编码的长度值
static const int CODE_LEN = 3;
/// 字符编码结构体
typedef struct {
int code[CODE_LEN]; // 保存编码的数组
int length; // 编码的长度
int weight; // 编码字符的权值
} HaffmanCode;
因为哈夫曼树结点数是确定的,所以采用顺序存储的结构实现二叉树,这样在节点访问上更加便利。
哈夫曼树结点除了二叉树结点必需的三个元素外,还包含了父结点指针、权值与一个标志位,这是为了方便后续向上遍历获取编码的过程。
除了定义树节点,还定义了一个编码结构体用来保存编码的信息,因为哈夫曼编码是不定长的编码。
2.2 构建哈夫曼树
/// 根据权重数组,构建哈夫曼树
/// @param weight 权值数组
/// @param n 数组个数
/// @param haffmanNodes 结点数组,顺序存储的哈夫曼树
Status buildHaffmanTree(int weight[], int n, HaffmanNode *haffmanNodes) {
// 1 将权值赋值到结点数组的前面结点中
for (int i = 0; i < 2 * n - 1; i++) {
if (i < n) {
haffmanNodes[i].weight = weight[i];
} else {
haffmanNodes[i].weight = 0;
}
// 初始化其他元素
haffmanNodes[i].parent = -1;
haffmanNodes[i].lch = -1;
haffmanNodes[i].rch = -1;
haffmanNodes[i].flag = 0;
}
// 2 前面已有 n 个叶子节点,下面构建 n - 1 个树枝结点
// 用来记录当前最小的两个权值
int min1, min2;
// 用来记录当前最小的两个权值的数组索引
int index1, index2;
for (int i = 0; i < n - 1; i++) {
// 2.1 初始化权值和索引
min1 = min2 = UINT16_MAX;
index1 = index2 = 0;
// 2.2 在当前 n 个叶子结点与新建的 i 个树枝结点中,
// 寻找两个最小权值,且未被添加到树中的结点
for (int j = 0; j < n + i; j++) {
HaffmanNode node = haffmanNodes[j];
if (node.weight < min1 && node.flag == 0) {
// 权值小于 min1 且未被添加到树中
// 将 min1 与 index1 值转移到 min2 和 index2 中
min2 = min1;
index2 = index1;
// min1 与 index1 记录新的最小权值结点
min1 = node.weight;
index1 = j;
} else if (node.weight < min2 && node.flag == 0) {
// 权值小于 min2 且未被添加到树中
min2 = node.weight;
index2 = j;
}
}
// 2.3 已找到两个最小权值的结点,构建新结点
haffmanNodes[n + i].weight = haffmanNodes[index1].weight + haffmanNodes[index2].weight;
haffmanNodes[n + i].lch = index1;
haffmanNodes[n + i].rch = index2;
// 2.4 修改找到的两个结点
// 修改父结点
haffmanNodes[index1].parent = n + i;
haffmanNodes[index2].parent = n + i;
// 修改标志位,表示已被添加到树中
haffmanNodes[index1].flag = 1;
haffmanNodes[index2].flag = 1;
}
return SUCCESS;
}
2.3 获取编码
/// 根据哈夫曼树获取编码值
/// @param haffmanNodes 结点数组,顺序存储的哈夫曼树
/// @param n 数组个数
/// @param haffmanCodes 编码数组
Status getHaffmanCode(HaffmanNode haffmanNodes[], int n, HaffmanCode haffmanCodes[]) {
// 声明一个编码结构体,用来保存临时数据
HaffmanCode code;
// 记录向上遍历的索引记录,通过判断左右子树决定编码 0 还是 1
int child, parent;
// 依次获取 n 个叶子结点的编码值
for (int i = 0; i < n; i++) {
code.length = 0;
code.weight = haffmanNodes[i].weight;
// 由叶子结点向根节点遍历,根节点的 parent 为 -1
child = i;
parent = haffmanNodes[child].parent;
while (parent != -1) {
if (child == haffmanNodes[parent].lch) {
// 是左子树,添加编码值 0
code.code[code.length] = 0;
} else {
// 是右子树,添加编码值 1
code.code[code.length] = 1;
}
// 编码长度加一
code.length++;
// 继续遍历更上一层
child = parent;
parent = haffmanNodes[child].parent;
}
// 完成编码的收集,但编码是倒序的,需要进行逆序
int maxIndex = code.length - 1;
for (int j = 0; j <= maxIndex; j++) {
haffmanCodes[i].code[j] = code.code[maxIndex - j];
}
// 保存权值与长度
haffmanCodes[i].weight = code.weight;
haffmanCodes[i].length = code.length;
}
return SUCCESS;
}
2.4 使用
int mainHaffmanTree() {
// 权值数组
int n = 4;
int weight[] = {2, 4, 5, 7};
// 创建结点数组,顺序存储哈夫曼二叉树,共有 2 * n - 1 个结点
// 其中有 n 个叶子结点表示各个权值,n - 1 个非叶子结点为新构建的权值结点
HaffmanNode *haffmanNodes = malloc(sizeof(HaffmanNode) * 2 * n - 1);
// 创建保存编码值的数组
HaffmanCode *haffmanCodes = malloc(sizeof(HaffmanCode) * n);
// 构建哈弗曼树
buildHaffmanTree(weight, n, haffmanNodes);
// 根据哈夫曼树获取编码值
getHaffmanCode(haffmanNodes, n, haffmanCodes);
// 打印编码值
int wpl = 0;
for (int i = 0; i < n; i++) {
HaffmanCode code = haffmanCodes[i];
printf("权值:%d 编码:", code.weight);
for (int j = 0; j < code.length; j++) {
printf("%d", code.code[j]);
}
printf("\n");
wpl += code.weight * code.length;
}
printf("哈夫曼树带权路径长度(WPL)为 %d\n", wpl);
return 0;
}
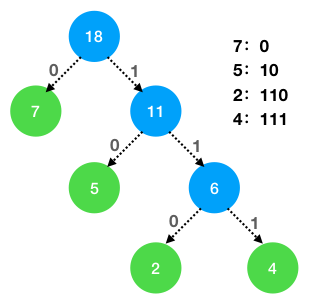
打印结果:
权值:2 编码:110
权值:4 编码:111
权值:5 编码:10
权值:7 编码:0
哈夫曼树带权路径长度(WPL)为 35
根据权值数组能轻易地得到哈夫曼树结构,如下图所示。根据树的结构,可以得到对应权值的编码值,与打印结果一致。