一、排序算法比较
衡量代码的好坏,包含两个重要指标:运行时间和占用空间。而时间复杂度代表运行时间,空间复杂度达标占用空间。空间复杂度是指算法在运行过程中临时占用存储空间大小的量度。常用的排序算法比较如下:
1. 稳定性
- 稳定: 冒泡排序、归并排序、插入排序、基数排序
- 不稳定:选择排序、快速选择排序、希尔排序、堆排序
2. 时间复杂度等比较
| 算法名 | 平均时间 | 最差情况 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) | B是真数(0-9),R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1<s<2 | 不稳定 | O(1) | s是所选分组 |
| 快速 | O(nlogn) | O(n2) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |
二、冒泡排序
1. 名字由来
比较任何两个相邻的项,如果第一个比第二个大,则交换他们。元素项向上移动至正确的顺序,就像气泡升至表面一样。
2. 算法描述
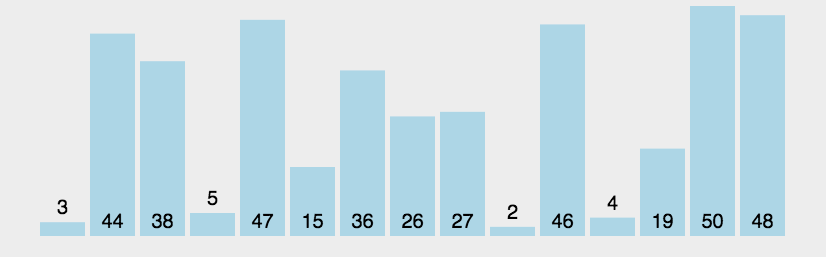
- 比较相邻的元素,如果前一个比后一个大,交换之
- 第一趟排序第1个和第2个一对,比较与交换,随后第2个和第3个一对比较交换,这样知道倒数第2个和最后1个,将最大的数移动到最后一位
- 第二趟将第二大的数移动到倒数第二位
- ............
- 因此需要 n-1 趟
3. 代码实现
export default (arr) =>{
//冒泡算法
for(let i = arr.length-1, tmp; i >0; i--){
for(let j = 0; j < i; j++){
tem = arr[j];
if(tmp > arr[j + 1]){
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
return arr;
}
4. 总结
冒泡排序是所有排序算法中最简单的。然而从运行时间的角度看,冒泡排序是最差的一个,所以不推荐使用该算法。其时间复杂度为 O(n2)。
三、选择排序
1. 介绍
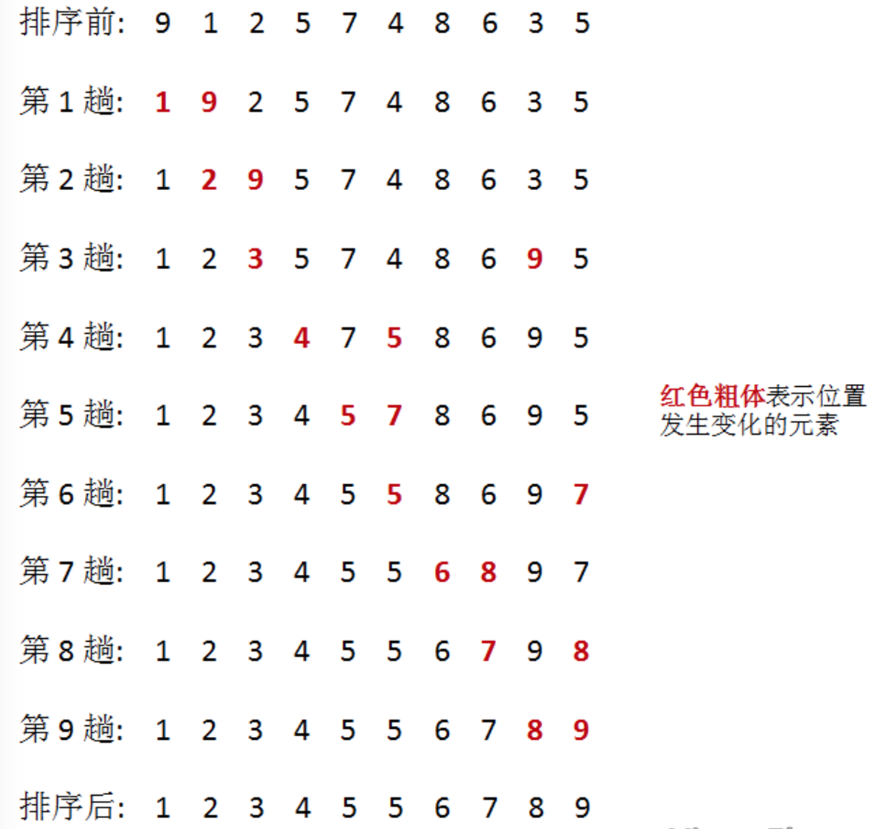
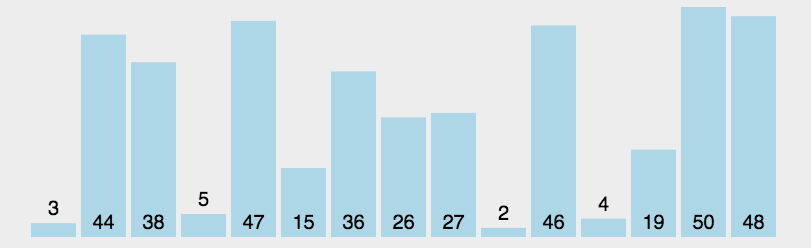
- 是一种原址比较排序算法
- 找到数据结构中的最小值并将其放置第一位,接着找到第二小的值并将其放在第二位。以此类推
2. 算法描述
3. 代码实现
export default (arr) => {
for(let i = 0, len = arr.length, min; i < len; i++){
min = arr[i];
for(let j = i + 1; j < len; j++){
if(arr[j] < min){
let c = min;
min = arr[j];
arr[j] = c;
}
}
arr[i] = min;
}
return arr;
}
4. 注意
选择排序同样也是一个复杂度为O(n2)的算法。和冒泡排序一样,它包含有嵌套的两个循环,这导致了二次方的复杂度。 接下来的插入排序会比选择排序的性能要好。
四、插入排序
1. 介绍
- 将一个记录插入到已排好序的序列中,从而得到一个新的有序序列
- 将序列的第一个数据看成是一个有序的子序列,然后从第二个记录逐个向该有序的子序列进行有序的插入,直至整个序列有序
2. 算法描述
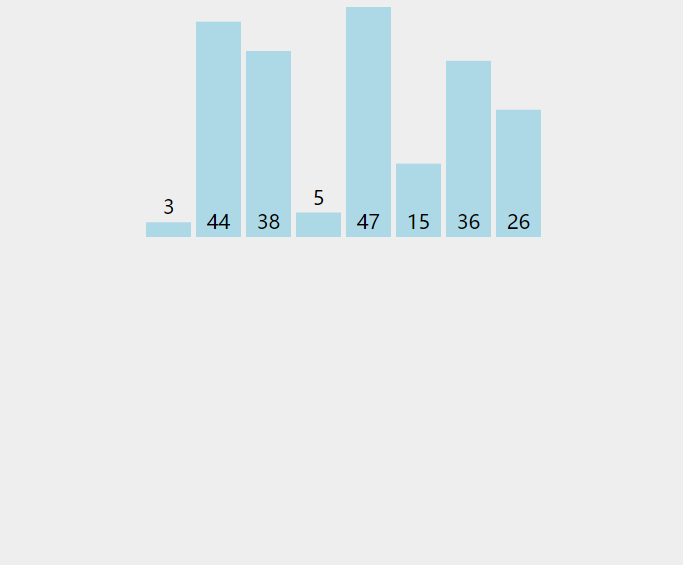
假设有一组无序序列 R0, R1, ... , RN-1。
(1) 我们先将这个序列中下标为 0 的元素视为元素个数为 1 的有序序列。
(2) 然后,我们要依次把 R1, R2, ... , RN-1 插入到这个有序序列中。所以,我们需要一个外部循环,从下标 1 扫描到 N-1 。
(3) 接下来描述插入过程。假设这是要将 Ri 插入到前面有序的序列中。由前面所述,我们可知,插入Ri时,前 i-1 个数肯定已经是有序了。
所以我们需要将Ri 和R0 ~ Ri-1 进行比较,确定要插入的合适位置。这就需要一个内部循环,我们一般是从后往前比较,即从下标 i-1 开始向 0 进行扫描。
3. 代码实现
export default (arr) => {
let len = arr.length, j, tmp;
for(let i = 0, i < len; i++){
j = i;
temp = arr[i];
while( j >0 && arr[j-1] > arr[j]){
arr[j] = arr[j-1];
j--;
}
arr[j] = temp;
}
return arr;
}
4. 总结
直接插入排序的过程中,不需要改变相等数值元素的位置,所以他是稳定的算法。排序小型的数组时,插入算法比选择排序和冒泡排序的性能要好。