RK 算法思路
这篇文章把RK算法的整个过程都进行了推导和分析.用问题的引导的形式来引导大家能有一个顺势的思考方向. 更加理解RK算法的精髓. 希望这篇文章能够让大家在RK算法上有所体会以及收获
回到字符匹配的经典问题,今天我们要来学习一个新的解决方案.
RK 算法的全称叫 Rabin-Karp 算法. 它是由两位发明者 Rabin 和 Karp 的名字来命名的算法. 这个算法理解不算过于复杂. 只是有一些编码技巧在里面,可以让我们学习;
在刚刚学习的BF算法中. 如果模式串长度为 m,主串长度为 n,那在主串中,就会有 n-m+1 个长度为 m 的子串,我们只需要暴力地对比这 n-m+1 个子串与模式串,就可以找出主串与模式串匹配的子串.
但是每次检查主串与子串是否匹配, 需要依次比对每个字符, 所以BF算法的时间复杂度比较高; 是O(n*m);
我们对BF的字符串匹配算法稍加改造,引入哈希算法,时间复杂度立刻就会降低.
RK 算法的思路是这样的:我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式匹配了.
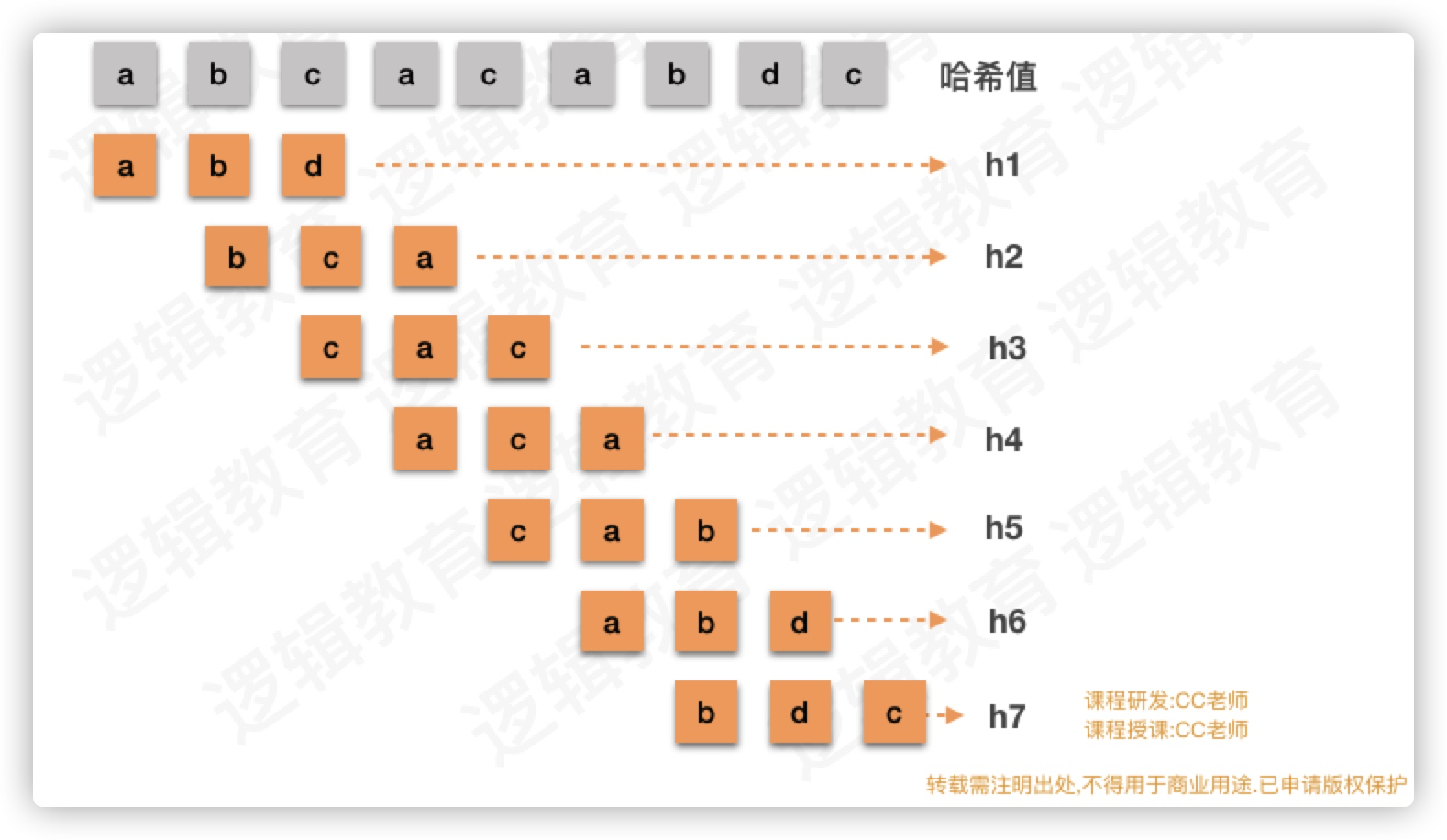

问题1: 如果把模式串与拆分后的子串换算成一个哈希值!

这时,我们需要设计一个转换哈希公式,关于散列/哈希公式的设计,我们会在后面的课程详细讲解. 这里不做深入的探讨!
关于哈希的安全手段,有兴趣的同学.可以学习逻辑教育的Hank老师的一套大课. 应用安全中,关于APP的防与护讲解的非常清楚;
简单说这里我们需要将不同的字符组合,能够映射出不同的数字. 数字的比较是单个值的比较,而字符的比较则需要逐个字符比较;

那么如何设计这样的一个公式了?
我们来看看数字的计算!

仔细观察发现:
- 6 是与 10 的2次方 相乘;
- 5 与 10 的1次方 相乘;
- 7 与 10 的0次方 相乘;
- 最终相加就得出了 657;

在这个过程中,我们如何将字母来进行匹配问题! 我们假设此时只考虑小写字母的情况!
问题: 首先如果把字母转化成数字?
可以把直接用ASC码吗? 不可以. 因为如果使用ASC码时,计算数字过大. 容易导出类型溢出;所以,我们要设计一个规则. 将字母-'a'的值单纯字母的对应的数字;
例如,字母'a'就是0 , 而字母'b'就是1; 以此类推!

问题: 小写字母存在多少进制?
十进制,一共有多少个数字组成? 是不是10个; 那么26个小写字母能组成多少进制? 26进制;
此时,我们就已经能将小写字母字符串换算成数字了! 而以下的计算方式就是我们的哈希公式!

为了方便大家的理解,CC老师特定用数字给大家做一个类似的推演. 直接用字母可能很多同学会转不过来! 这是单纯为了让你理解. 而设计的小例子;

大家可以看到. 我们能够把65127451234 按照模式串的长度m=3,分解成以下这么多小的子串. 首先需要将123转化成哈希值;
我们可以看的数字的哈希转化和字母的转换是一个道理. 那接下来,我们用代码来实现模式串的哈希值求解;
那为了方便,在求解模式串的计算,也可以一滩水把主串中的第一个拆解的子串计算.
int RK(char *S, char *P)
{
//1. n:主串长度, m:子串长度
int m = (int) strlen(P);
int n = (int) strlen(S);
printf("主串长度为:%d,子串长度为:%d\n",n,m);
//A.模式串的哈希值; St.主串分解子串的哈希值;
unsigned int A = 0;
unsigned int St = 0;
//2.求得子串与主串中0~m字符串的哈希值[计算子串与主串0-m的哈希值]
//循环[0,m)获取模式串A的HashValue以及主串第一个[0,m)的HashValue
//此时主串:"abcaadddabceeffccdd" 它的[0,2)是ab
//此时模式串:"cc"
//cc = 2 * 26^1 + 2 *26 ^0 = 52+2 = 54;
//ab = 0 * 26^1 + 1 *26^0 = 0+1 = 1;
for(int i = 0; i != m; i++){
//第一次 A = 0*26+2;
//第二次 A = 2*26+2;
A = (d*A + (P[i] - 'a'));
//第一次 st = 0*26+0
//第二次 st = 0*26+1
St = (d*St + (S[i] - 'a'));
}
...
问题2 主串拆解的子串与模式串的哈希值比较?

问题: 那么如何拆解主串,并且求解出它的哈希值?
解决方案1: 把主串按照模式串长度m,拆解成n/m份,然后按照刚刚求解子串哈希值的循环把每个哈希值求解后,存储到数组中?
这个方案,可行吗? 可行! 但是高效吗? 不高效! 所以,我们看看其他求解方案:
解决方案2: 大家注意了没有CC老师,在求解模式串的哈希值,就一起把主串拆解的第一个子串的哈希值一起求解了;
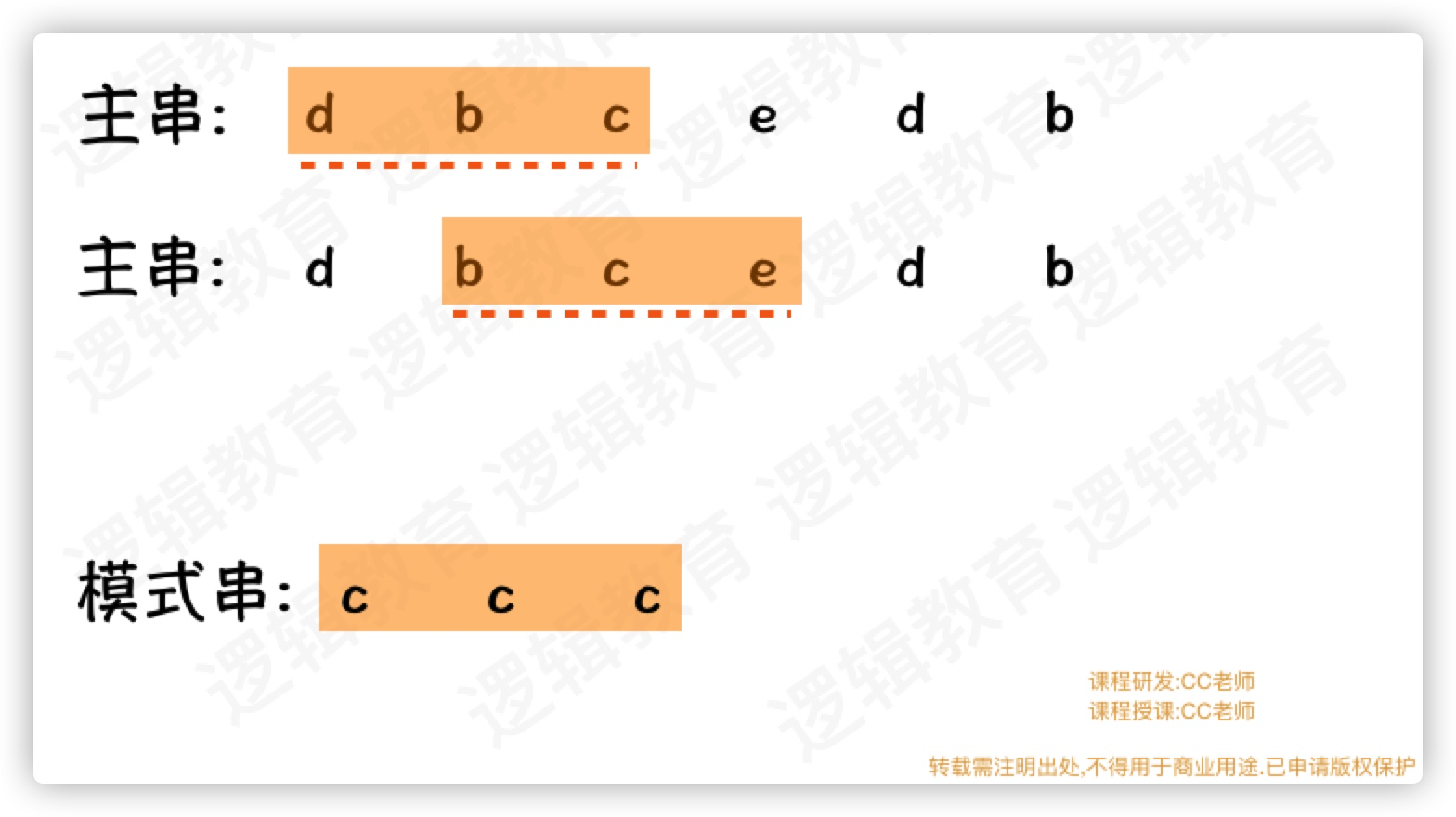
注意观察,我们第一个对比主串'dbc'的哈希值与模式串'ccc'的哈希值不一致时,我们会讲模式串往后移动一位,也就是用'bce'的哈希值来与'ccc' 比较.
那么我可不可以一边计算主串拆解子串的哈希值,一边比较了? 可以吗? 当然可以!
这样的好处是什么?
- 这样我们就不需要额外写一个循环,并且还有需要额外的存储空间来存储这些哈希值.
- 当我们找到与模式串匹配的值,就不需要在继续计算后面的哈希值,节省了不必要的计算;
问题: 那么主串的拆解子串与子串之间有什么关系了?
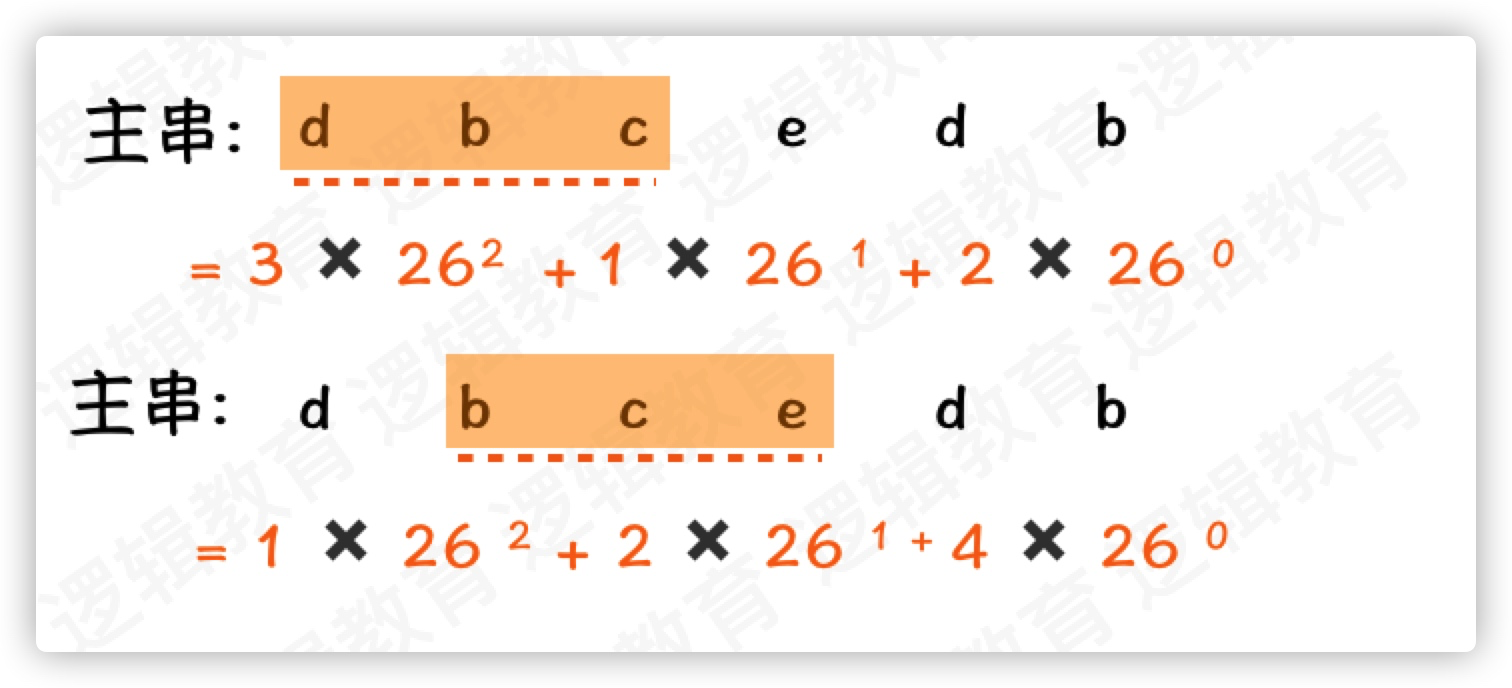
子串哈希值求解规律:



这个规律已经推演的非常清楚. 那么我们来到一个串的场景;
问题: 当 i=0 时,此时127 这个子串的哈希值有没有求解出来 ?
当然求解出来了.在我们求解模式串时就一并把主串拆解的第一个子串的哈希值就已经求解的;
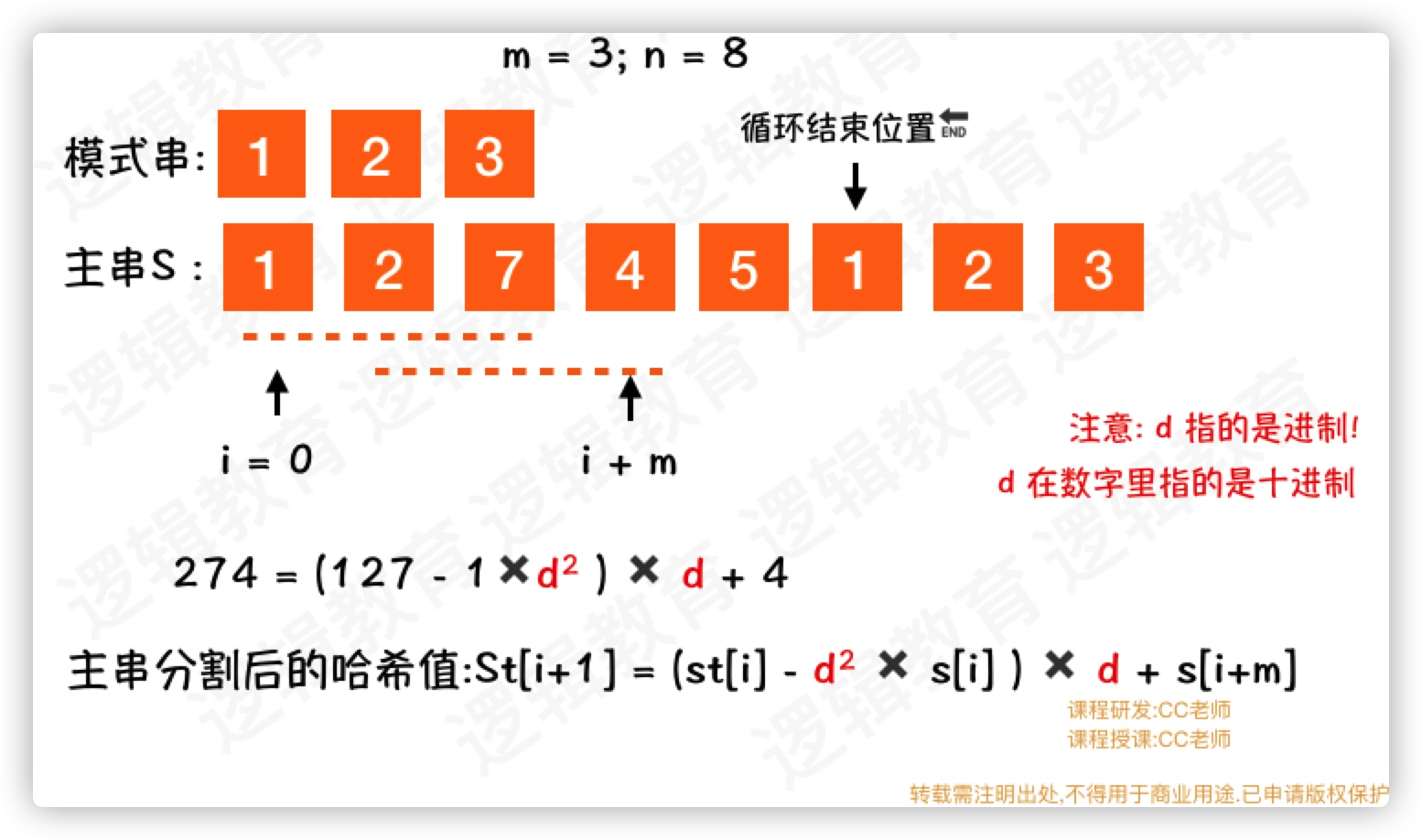
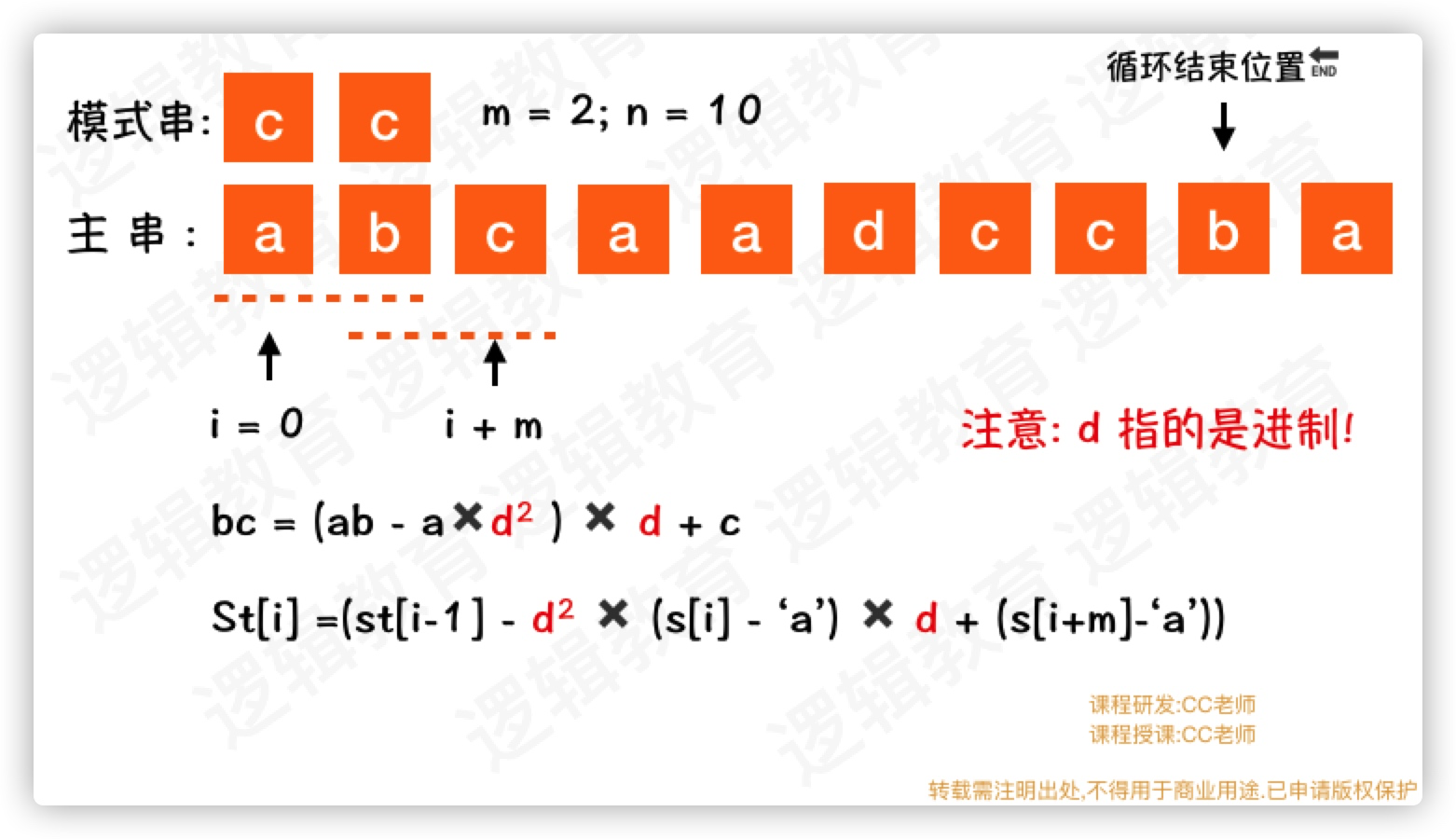
- 接下来,我们要借助开始一层遍历; 从
0开始到n-m结束; - 同时在比较
st[0]与 模式串哈希值时,如果匹配成功,则退出循环.返回当前的i值; - 否则,借助
st[0]的值求解St[1]的值;
在刚刚的图中,你可以发现我们每次求解哈希值是都要用的d^2次方;
d^2 此时,其实就是 d^(m-1)次方.那么可以提前计算好.在这个循环里就直接使用就可以了. 所以设计一个函数,用来求解d^(m-1)次方
//3.算出最d进制下的最高位
//d^(m-1)位的值;
int getMaxValue(int m){
int h = 1;
for(int i = 0;i < m - 1;i++){
h = (h*d);
}
return h;
}
那么接下来,就开始实现关于RK算法的核心.主串的子串哈希值求解并去模式串哈希值比较的过程!
int RK(char *S, char *P)
{
//1. n:主串长度, m:子串长度
int m = (int) strlen(P);
int n = (int) strlen(S);
printf("主串长度为:%d,子串长度为:%d\n",n,m);
//A.模式串的哈希值; St.主串分解子串的哈希值;
unsigned int A = 0;
unsigned int St = 0;
//2.求得子串与主串中0~m字符串的哈希值[计算子串与主串0-m的哈希值]
//循环[0,m)获取模式串A的HashValue以及主串第一个[0,m)的HashValue
//此时主串:"abcaadddabceeffccdd" 它的[0,2)是ab
//此时模式串:"cc"
//cc = 2 * 26^1 + 2 *26 ^0 = 52+2 = 54;
//ab = 0 * 26^1 + 1 *26^0 = 0+1 = 1;
for(int i = 0; i != m; i++){
//第一次 A = 0*26+2;
//第二次 A = 2*26+2;
A = (d*A + (P[i] - 'a'));
//第一次 st = 0*26+0
//第二次 st = 0*26+1
St = (d*St + (S[i] - 'a'));
}
//3. 获取d^m-1值(因为经常要用d^m-1进制值)
int hValue = getMaxValue(m);
//4.遍历[0,n-m], 判断模式串HashValue A是否和其他子串的HashValue 一致.
//不一致则继续求得下一个HashValue
//如果一致则进行二次确认判断,2个字符串是否真正相等.反正哈希值冲突导致错误
//注意细节:
//① 在进入循环时,就已经得到子串的哈希值以及主串的[0,m)的哈希值,可以直接进行第一轮比较;
//② 哈希值相等后,再次用字符串进行比较.防止哈希值冲突;
//③ 如果不相等,利用在循环之前已经计算好的st[0] 来计算后面的st[1];
//④ 在对比过程,并不是一次性把所有的主串子串都求解好Hash值. 而是是借助s[i]来求解s[i+1] . 简单说就是一边比较哈希值,一边计算哈希值;
for(int i = 0; i <= n-m; i++){
if(A == St)
return i;
St = ((St - hValue*(S[i]-'a'))*d + (S[i+m]-'a'));
}
return -1;
}
问题3: 哈希冲突
在刚刚的课程中,我们涉及到哈希. 就有可能遇到不同的字母使用同一个公式,导致哈希冲突. 那么我们改如果解决这个问题了?

关于哈希冲突,有很多的解决方案; 比如我们可以增加哈希公式的复杂度. 也还有很多其他方案.关于哈希冲突的方式,在我们的后续的课程里会单独讲解. 这个在这里不做深入探索;
那么除了这个方式有其他的办法吗?
其实有一个非常简单的办法!

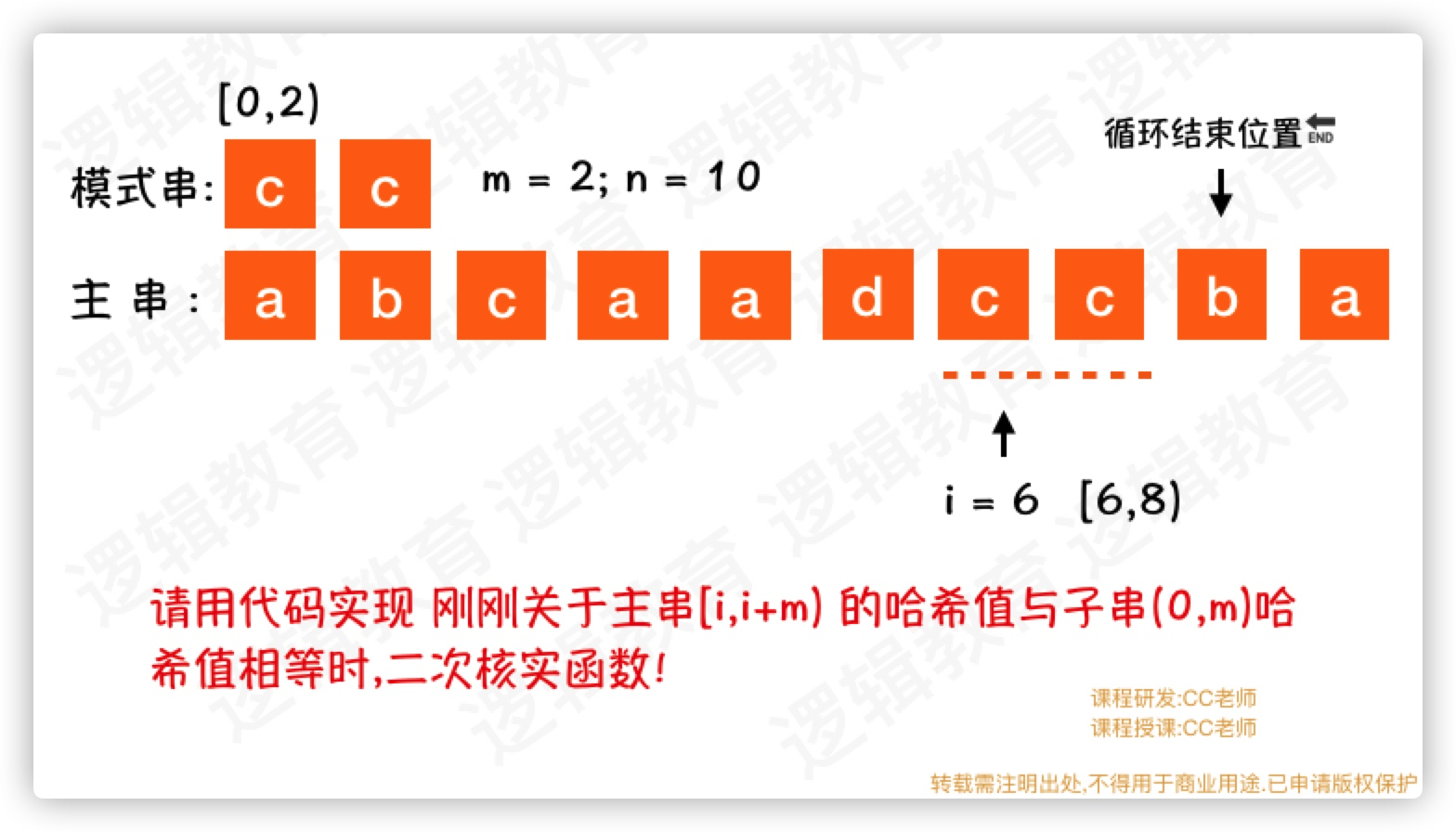
代码实现:
//4.为了杜绝哈希冲突. 当前发现模式串和子串的HashValue 是一样的时候.还是需要二次确认2个字符串是否相等.
int isMatch(char *S, int i, char *P, int m)
{
int is, ip;
for(is=i, ip=0; is != m && ip != m; is++, ip++)
if(S[is] != P[ip])
return 0;
return 1;
}
最后在RK 算法中,for 循环中间
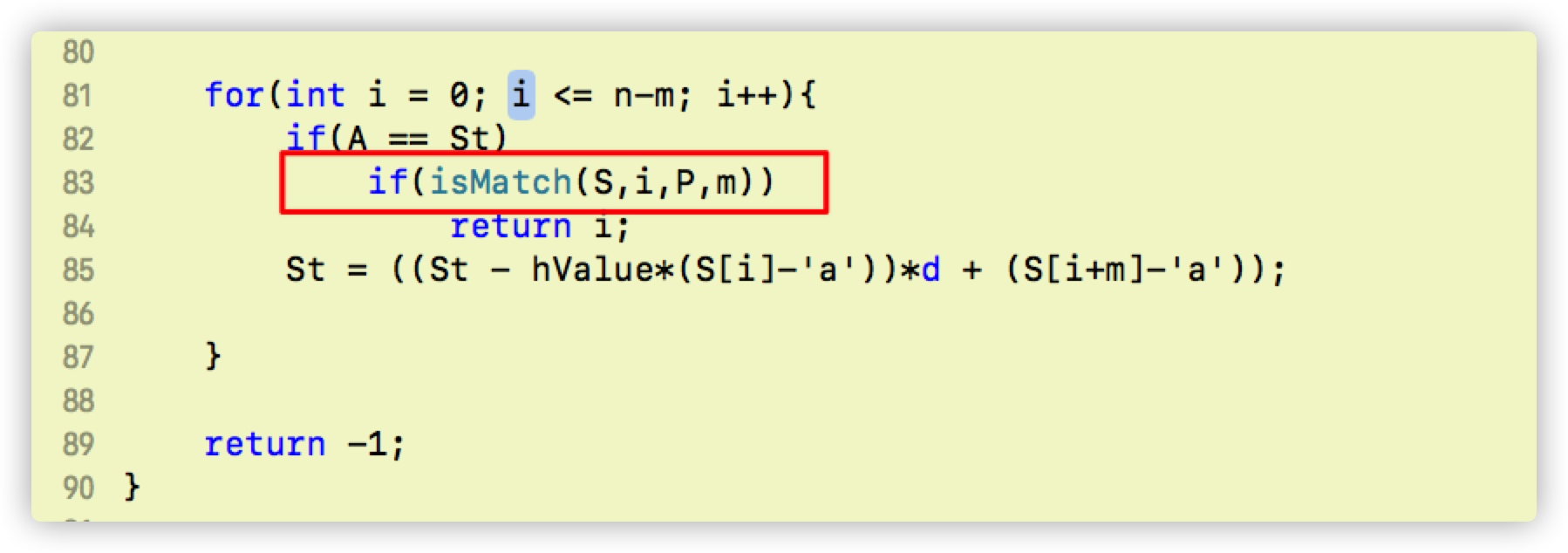
RK 算法完成代码实现
//
// main.c
// 003--RK匹配算法
//
// Created by CC老师 on 2019/10/29.
// Copyright © 2019年 CC老师. All rights reserved.
//
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//d 表示进制
#define d 26
//4.为了杜绝哈希冲突. 当前发现模式串和子串的HashValue 是一样的时候.还是需要二次确认2个字符串是否相等.
int isMatch(char *S, int i, char *P, int m)
{
int is, ip;
for(is=i, ip=0; is != m && ip != m; is++, ip++)
if(S[is] != P[ip])
return 0;
return 1;
}
//3.算出最d进制下的最高位
//d^(m-1)位的值;
int getMaxValue(int m){
int h = 1;
for(int i = 0;i < m - 1;i++){
h = (h*d);
}
return h;
}
/*
* 字符串匹配的RK算法
* Author:Rabin & Karp
* 若成功匹配返回主串中的偏移,否则返回-1
*/
int RK(char *S, char *P)
{
//1. n:主串长度, m:子串长度
int m = (int) strlen(P);
int n = (int) strlen(S);
printf("主串长度为:%d,子串长度为:%d\n",n,m);
//A.模式串的哈希值; St.主串分解子串的哈希值;
unsigned int A = 0;
unsigned int St = 0;
//2.求得子串与主串中0~m字符串的哈希值[计算子串与主串0-m的哈希值]
//循环[0,m)获取模式串A的HashValue以及主串第一个[0,m)的HashValue
//此时主串:"abcaadddabceeffccdd" 它的[0,2)是ab
//此时模式串:"cc"
//cc = 2 * 26^1 + 2 *26 ^0 = 52+2 = 54;
//ab = 0 * 26^1 + 1 *26^0 = 0+1 = 1;
for(int i = 0; i != m; i++){
//第一次 A = 0*26+2;
//第二次 A = 2*26+2;
A = (d*A + (P[i] - 'a'));
//第一次 st = 0*26+0
//第二次 st = 0*26+1
St = (d*St + (S[i] - 'a'));
}
//3. 获取d^m-1值(因为经常要用d^m-1进制值)
int hValue = getMaxValue(m);
//4.遍历[0,n-m], 判断模式串HashValue A是否和其他子串的HashValue 一致.
//不一致则继续求得下一个HashValue
//如果一致则进行二次确认判断,2个字符串是否真正相等.反正哈希值冲突导致错误
//注意细节:
//① 在进入循环时,就已经得到子串的哈希值以及主串的[0,m)的哈希值,可以直接进行第一轮比较;
//② 哈希值相等后,再次用字符串进行比较.防止哈希值冲突;
//③ 如果不相等,利用在循环之前已经计算好的st[0] 来计算后面的st[1];
//④ 在对比过程,并不是一次性把所有的主串子串都求解好Hash值. 而是是借助s[i]来求解s[i+1] . 简单说就是一边比较哈希值,一边计算哈希值;
for(int i = 0; i <= n-m; i++){
if(A == St)
if(isMatch(S,i,P,m))
return i;
St = ((St - hValue*(S[i]-'a'))*d + (S[i+m]-'a'));
}
return -1;
}
int main()
{
char *buf="abcaadddabceeffccdd";
char *ptrn="cc";
printf("主串为%s\n",buf);
printf("子串为%s\n",ptrn);
int index = RK(buf, ptrn);
printf("find index : %d\n",index);
return 1;
}