视频面试超高频在线编程题，搞懂这些足以应对大部分公司

引言

现在大厂面试几乎都会问到算法，回答不上来会让你在面试官前大打折扣。前端怎么进阶算法喃？

本周是瓶子君前端进阶算法的第三周🎉🎉🎉，这里，会带你 从 0 到 1 构建完整的前端数据结构与算法体系。

本周已经不单是简单的链表操作（一般链表的问题可以考虑使用快慢指针），开始涉及五大常用算法策略、二叉树、Trie树、队列等，这里仅作为入门，后面会详细介绍，发散思维，你会发现面试中的算法、开发中的算法真的很 easy。

往期精彩系列

• 10问10答，带你快速入门前端算法
• 前端进阶算法4：链表原来如此简单（+leetcode刷题）
• 前端进阶算法3：从浏览器缓存淘汰策略和Vue的keep-alive学习LRU算法
• 瓶子君前端进阶算法营首周总结
• 前端进阶算法2：从Chrome V8源码看JavaScript数组（附赠腾讯面试题）
• 前端进阶算法1：如何分析、统计算法的执行效率和资源消耗？

以及题目：

• 图解leetcode88：合并两个有序数组
• 字节&leetcode1：两数之和
• 腾讯：数组扁平化、去重、排序
• leetcode349：给定两个数组，编写一个函数来计算它们的交集
• leetcode146：设计和实现一个LRU（最近最少使用）缓存机制
• 阿里算法题：编写一个函数计算多个数组的交集
• leetcode21：合并两个有序链表
• 有赞&leetcode141：判断一个单链表是否有环
• 图解leetcode206：反转链表
• leetcode876：求链表的中间结点
• leetcode19：删除链表倒数第 n 个结点
• 图解字节&leetcode160：编写一个程序，找到两个单链表相交的起始节点
• 图解字节&leetcode151：翻转字符串里的单词
• 图解leetcode14：最长公共前缀

本节是第三周的总结与回顾，下面开始进入正题吧！👇👇👇

一、图解字节&拼多多&leetcode14：最长公共前缀

1. 题目

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"

示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

2. 答案

解法一：逐个比较

解题思路： 从前往后一次比较字符串，获取公共前缀

画图帮助理解一下：

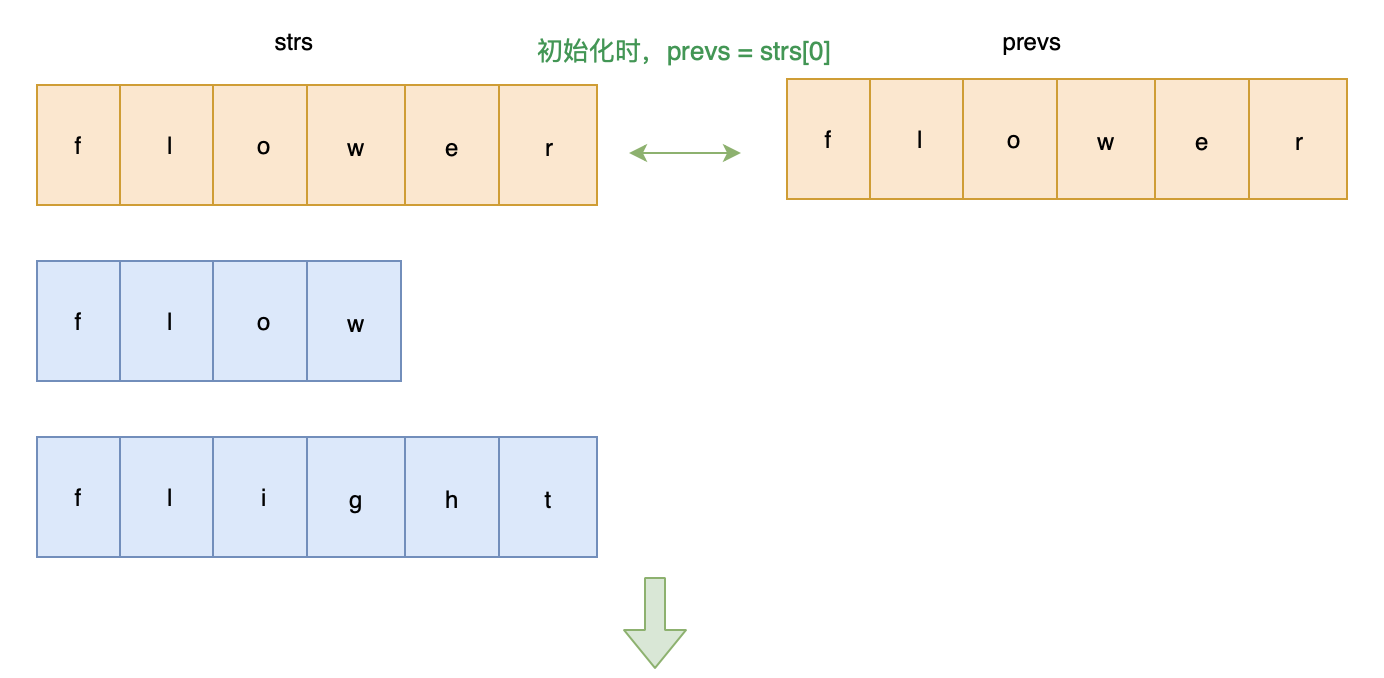
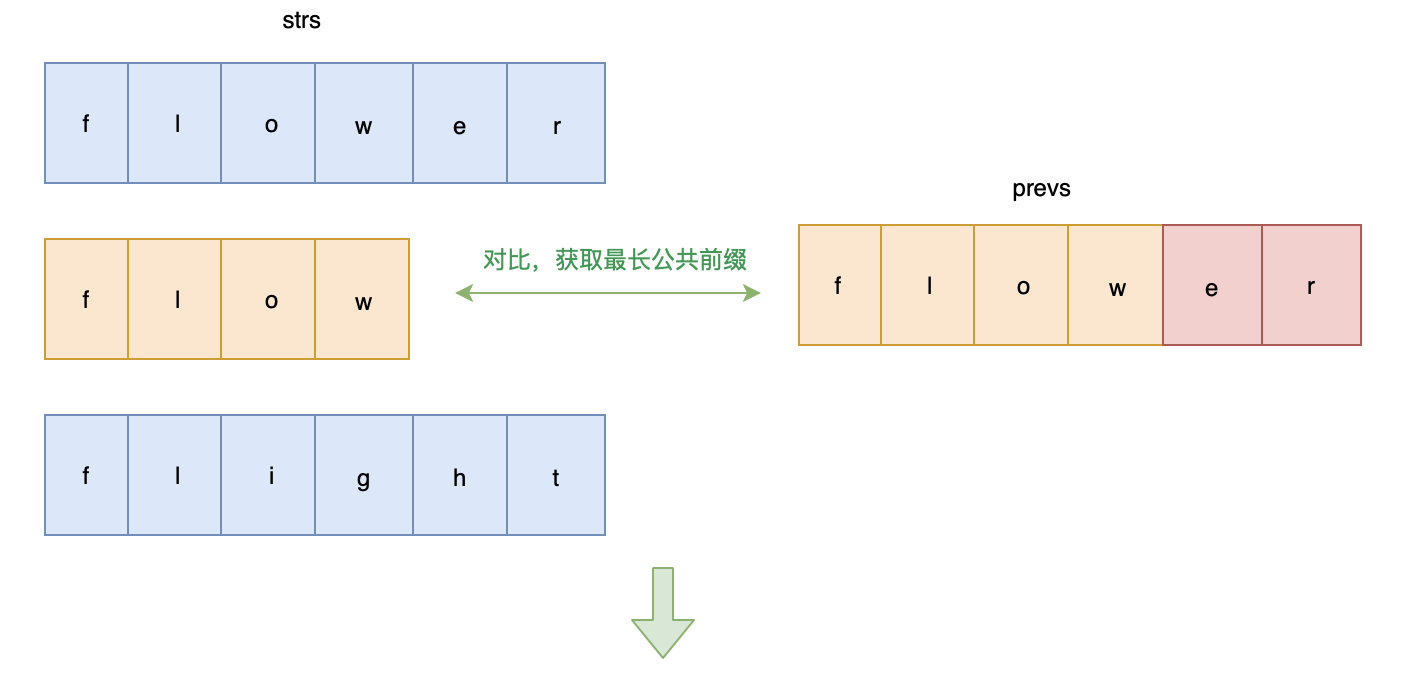
代码实现：

var longestCommonPrefix = function(strs) {
    if (strs === null || strs.length === 0) return "";
    let prevs = strs[0]
    for(let i = 1; i < strs.length; i++) {
        let j = 0
        for(; j < prevs.length && j < strs[i].length; j++) {
            if(prevs.charAt(j) !== strs[i].charAt(j)) break
        }
        prevs = prevs.substring(0, j)
        if(prevs === "") return ""
    }
    return prevs
};

时间复杂度：O(s)，s 是所有字符串中字符数量的总和

空间复杂度：O(1)

解法二：仅需最大、最小字符串的最长公共前缀

解题思路： 获取数组中的最大值及最小值字符串，最小字符串与最大字符串的最长公共前缀也为其他字符串的公共前缀，即为字符串数组的最长公共前缀

例如 abc 、 abcd 、ab 、ac ，最小 ab 与最大 ac 的最长公共前缀一定也是 abc 、 abcd 的公共前缀

画图帮助理解一下：

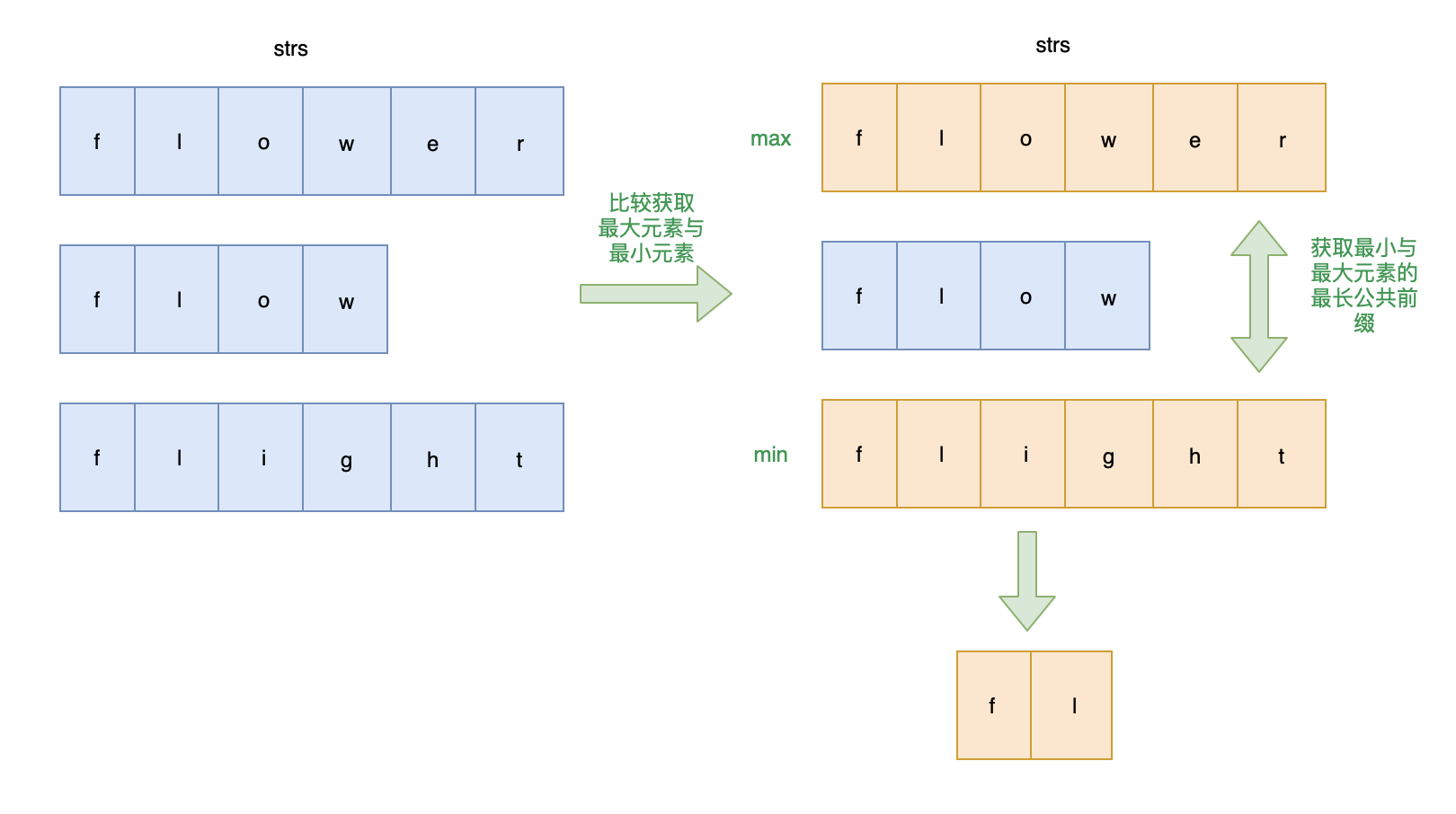
代码实现：

var longestCommonPrefix = function(strs) {
    if (strs === null || strs.length === 0) return "";
    if(strs.length === 1) return strs[0]
    let min = 0, max = 0
    for(let i = 1; i < strs.length; i++) {
        if(strs[min] > strs[i]) min = i
        if(strs[max] < strs[i]) max = i
    }
    for(let j = 0; j < strs[min].length; j++) {
        if(strs[min].charAt(j) !== strs[max].charAt(j)) {
            return strs[min].substring(0, j)
        }
    }
    return strs[min]
};

时间复杂度：O(n+m)，n是数组的长度， m 是字符串数组中最短字符的长度

空间复杂度：O(1)

解法三：分治策略 归并思想

分治，顾名思义，就是分而治之，将一个复杂的问题，分成两个或多个相似的子问题，在把子问题分成更小的子问题，直到更小的子问题可以简单求解，求解子问题，则原问题的解则为子问题解的合并。

这道题就是一个典型的分治策略问题：

• 问题：求多个字符串的最长公共前缀
• 分解成多个相似的子问题：求两个字符串的最长公共前缀
• 子问题可以简单求解：两个字符串的最长公共前缀求解很简单
• 原问题的解为子问题解的合并：多个字符串的最长公共前缀为两两字符串的最长公共前缀的最长公共前缀，我们可以归并比较两最长公共前缀字符串的最长公共前缀，知道最后归并比较成一个，则为字符串数组的最长公共前缀：LCP(S1, S2, ..., Sn) = LCP(LCP(S1, Sk), LCP(Sk+1, Sn))

画图帮助理解一下：

以 abc 、 abcd 、ab 、ac 为例：

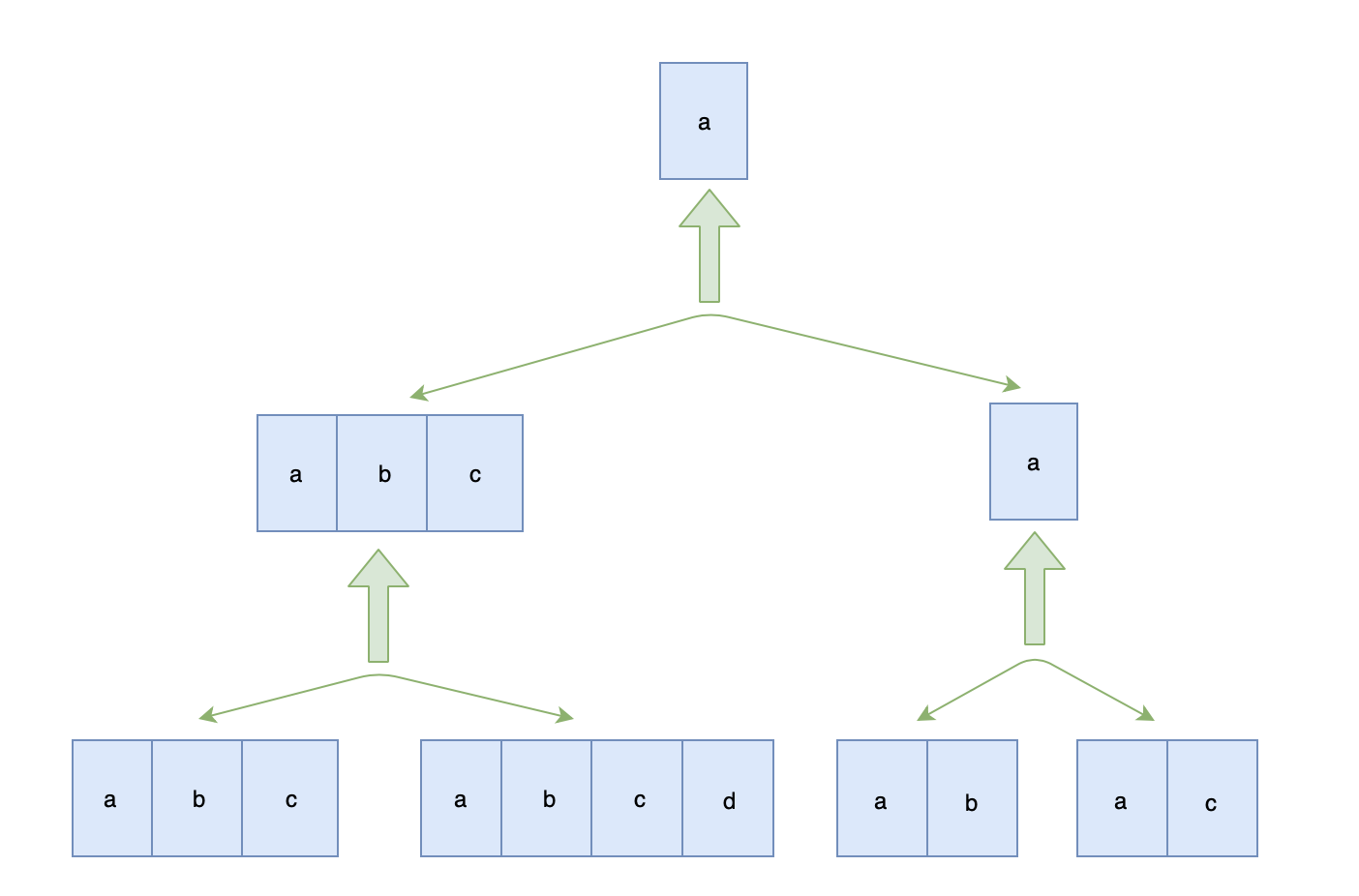
代码实现：

var longestCommonPrefix = function(strs) {
    if (strs === null || strs.length === 0) return "";
    return lCPrefixRec(strs)
};

// 若分裂后的两个数组长度不为 1，则继续分裂
// 直到分裂后的数组长度都为 1，
// 然后比较获取最长公共前缀
function lCPrefixRec(arr) {
  let length = arr.length
  if(length === 1) {
    return arr[0]
  }
  let mid = Math.floor(length / 2),
      left = arr.slice(0, mid),
      right = arr.slice(mid, length)
  return lCPrefixTwo(lCPrefixRec(left), lCPrefixRec(right))
}

// 求 str1 与 str2 的最长公共前缀
function lCPrefixTwo(str1, str2) {
    let j = 0
    for(; j < str1.length && j < str2.length; j++) {
        if(str1.charAt(j) !== str2.charAt(j)) {
            break
        }
    }
    return str1.substring(0, j)
}

时间复杂度：O(s)，s 是所有字符串中字符数量的总和

空间复杂度：O(m*logn)，n是数组的长度，m为字符串数组中最长字符的长度

解法四：Trie 树（字典树）

Trie 树，也称为字典树或前缀树，顾名思义，它是用来处理字符串匹配问题的数据结构，以及用来解决集合中查找固定前缀字符串的数据结构。

解题思路： 构建一个 Trie 树，字符串数组的最长公共序列就为从根节点开始遍历树，直到：

• 遍历节点存在超过一个子节点的节点

• 或遍历节点为一个字符串的结束字符

为止，走过的字符为字符串数组的最长公共前缀

画图帮助理解一下：

构建一个 Trie 树，以 abc 、 abcd 、ab 、ac 为例：

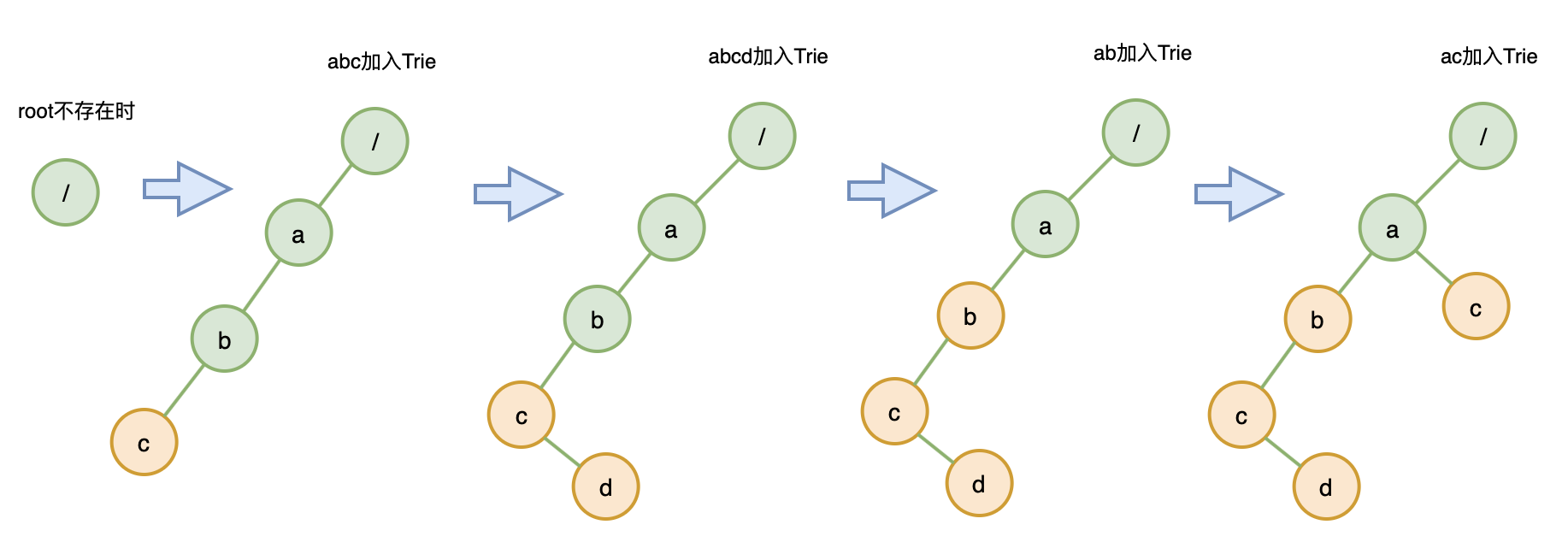
代码实现：

var longestCommonPrefix = function(strs) {
    if (strs === null || strs.length === 0) return "";
    // 初始化 Trie 树
    let trie = new Trie()
    // 构建 Trie 树
    for(let i = 0; i < strs.length; i++) {
        if(!trie.insert(strs[i])) return ""
    }
    // 返回最长公共前缀
    return trie.searchLongestPrefix()
};
// Trie 树
var Trie = function() {
    this.root = new TrieNode()
};
var TrieNode = function() {
    // next 放入当前节点的子节点
    this.next = {};
    // 当前是否是结束节点
    this.isEnd = false;
};
Trie.prototype.insert = function(word) {
    if (!word) return false
    let node = this.root
    for (let i = 0; i < word.length; i++) {
        if (!node.next[word[i]]) {
            node.next[word[i]] = new TrieNode()
        }
        node = node.next[word[i]]
    }
    node.isEnd = true
    return true
};
Trie.prototype.searchLongestPrefix = function() {
    let node = this.root
    let prevs = ''
    while(node.next) {
        let keys = Object.keys(node.next)
        if(keys.length !== 1) break
        if(node.next[keys[0]].isEnd) {
            prevs += keys[0]
            break
        }
        prevs += keys[0]
        node = node.next[keys[0]]
    }
    return prevs
}

时间复杂度：O(s+m)，s 是所有字符串中字符数量的总和，m为字符串数组中最长字符的长度，构建 Trie 树需要 O(s) ，最长公共前缀查询操作的复杂度为 O(m)

空间复杂度：O(s)，用于构建 Trie 树 leetcode

3. 更多解法请看 图解字节&leetcode14：最长公共前缀

二、图解字节&leetcode151：翻转字符串里的单词

1. 题目

给定一个字符串，逐个翻转字符串中的每个单词。

示例 1：

输入: "the sky is blue"
输出: "blue is sky the"

示例 2：

输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

说明：

• 无空格字符构成一个单词。
• 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
• 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

2. 答案

解法一：正则 + JS API

var reverseWords = function(s) {
    return s.trim().replace(/\s+/g, ' ').split(' ').reverse().join(' ')
};

解法二：双端队列（不使用 API）

双端队列，故名思义就是两端都可以进队的队列

解题思路：

• 首先去除字符串左右空格
• 逐个读取字符串中的每个单词，依次放入双端队列的对头
• 再将队列转换成字符串输出（已空格为分隔符）

画图理解：

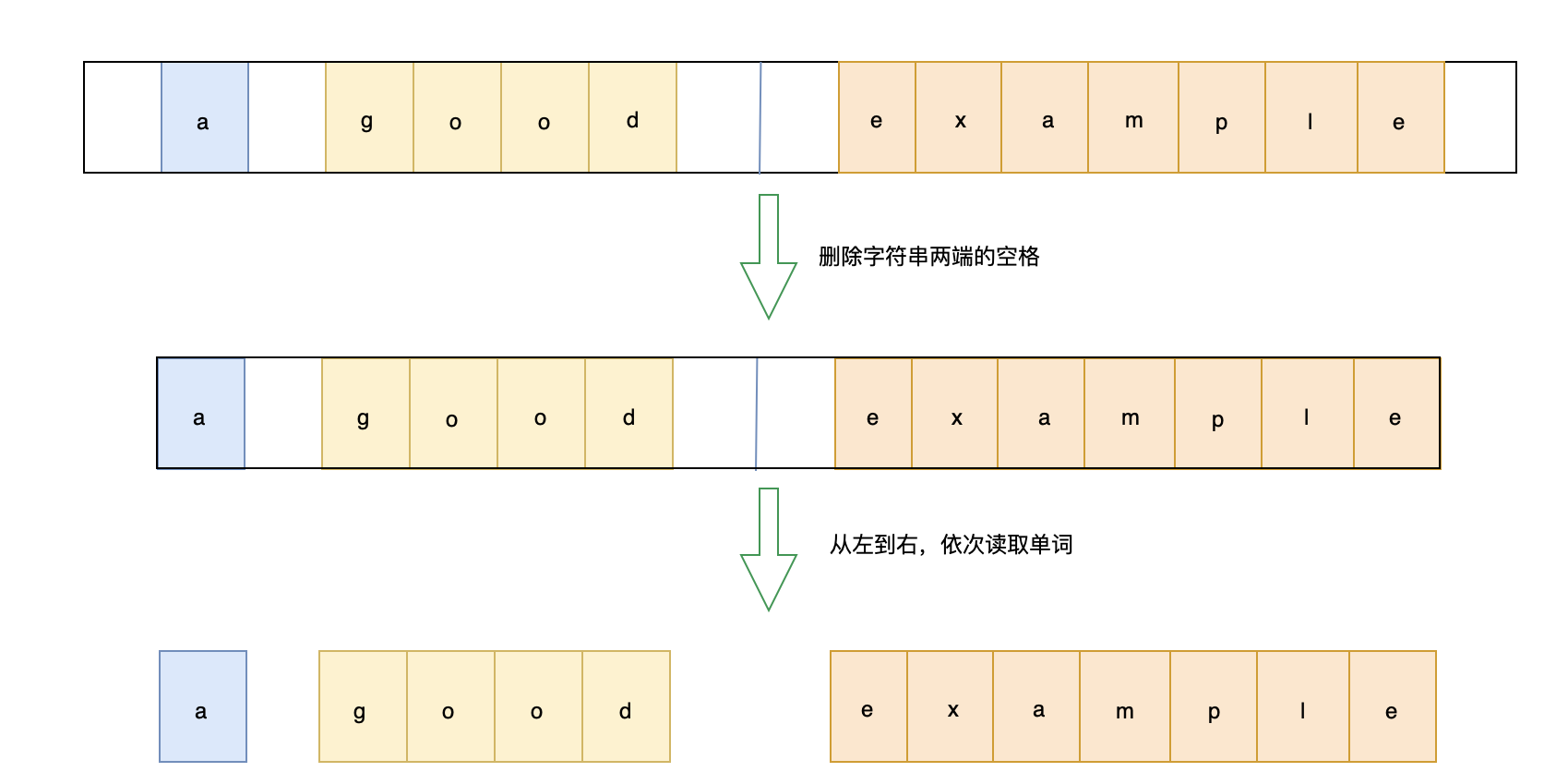
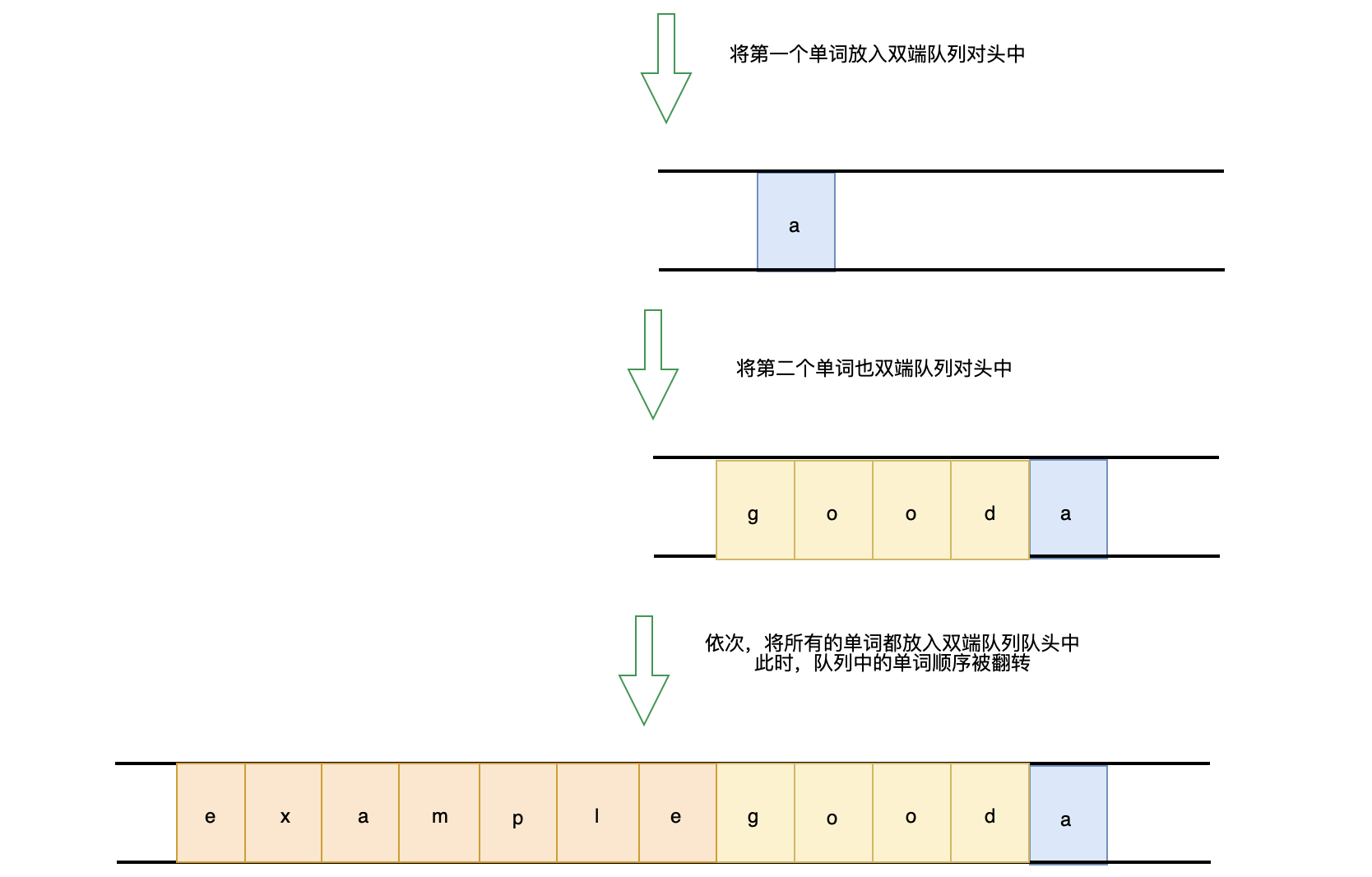
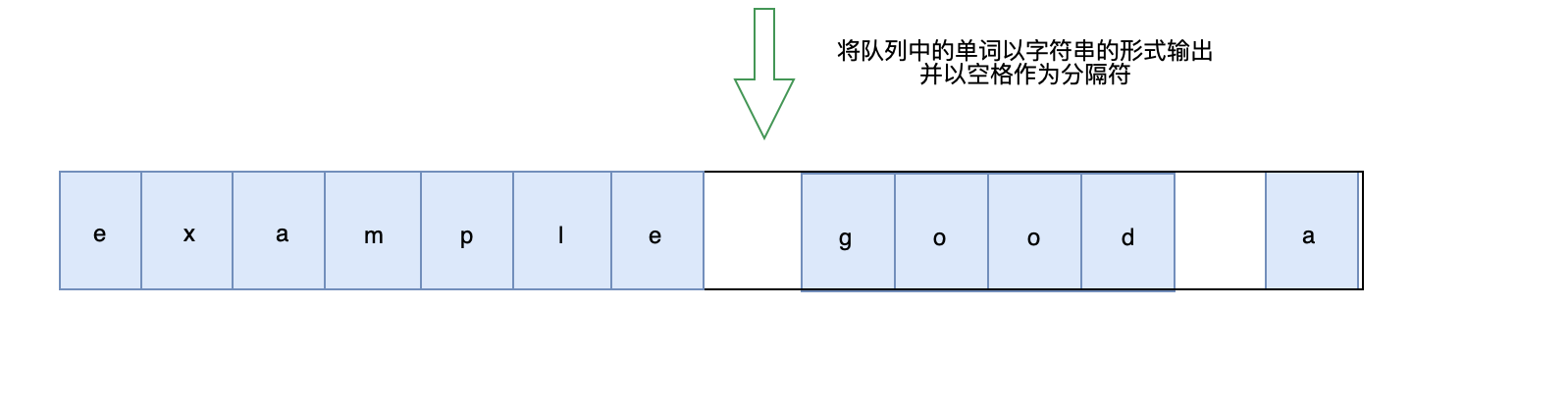
代码实现：

var reverseWords = function(s) {
    let left = 0
    let right = s.length - 1
    let queue = []
    let word = ''
    while (s.charAt(left) === ' ') left ++
    while (s.charAt(right) === ' ') right --
    while (left <= right) {
        let char = s.charAt(left)
        if (char === ' ' && word) {
            queue.unshift(word)
            word = ''
        } else if (char !== ' '){
            word += char
        }
        left++
    }
    queue.unshift(word)
    return queue.join(' ')
};

leetcode

3. 更多解法请看 图解字节&leetcode151：翻转字符串里的单词

三、图解字节&leetcode160：编写一个程序，找到两个单链表相交的起始节点

1. 题目

编写一个程序，找到两个单链表相交的起始节点。

如下面的两个链表：

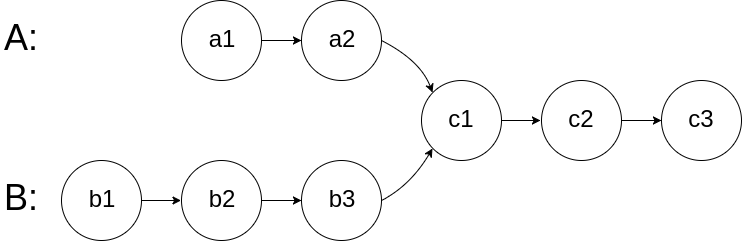
在节点 c1 开始相交。

示例 1：

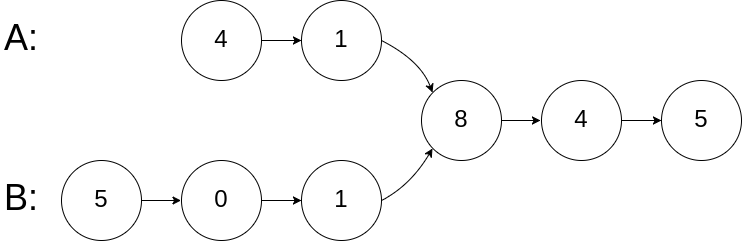
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

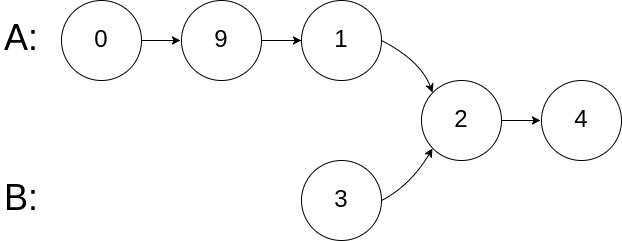
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Reference of the node with value = 2
输入解释：相交节点的值为 2 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

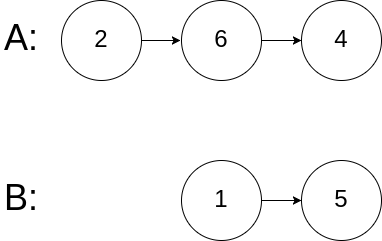
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
解释：这两个链表不相交，因此返回 null。

注意：

• 如果两个链表没有交点，返回 null.
• 在返回结果后，两个链表仍须保持原有的结构。
• 可假定整个链表结构中没有循环。
• 程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

2. 答案

解法一：标记法(简单但空间复杂度为O(n)，不符合，仅做参考)

解题思路： 两次遍历，先遍历一个链表，给链表中的每个节点都增加一个标志位，然后遍历另外一个链表，遍历到第一个已被标志过的节点为两链表相交的起始节点。

若遍历完都没有发现已被标志过的节点，则两链表不相交，返回 null

var getIntersectionNode = function(headA, headB) {
    while(headA) {
        headA.flag = true
        headA = headA.next
    }
    while(headB) {
        if (headB.flag) return headB
        headB = headB.next
    }
    return null
};

时间复杂度：O(n)

空间复杂度：O(n)

解法二：双指针法

解题思路： 如果 A、B 两链表相交，则 A 、B 自相交点往后的链表是一致的。

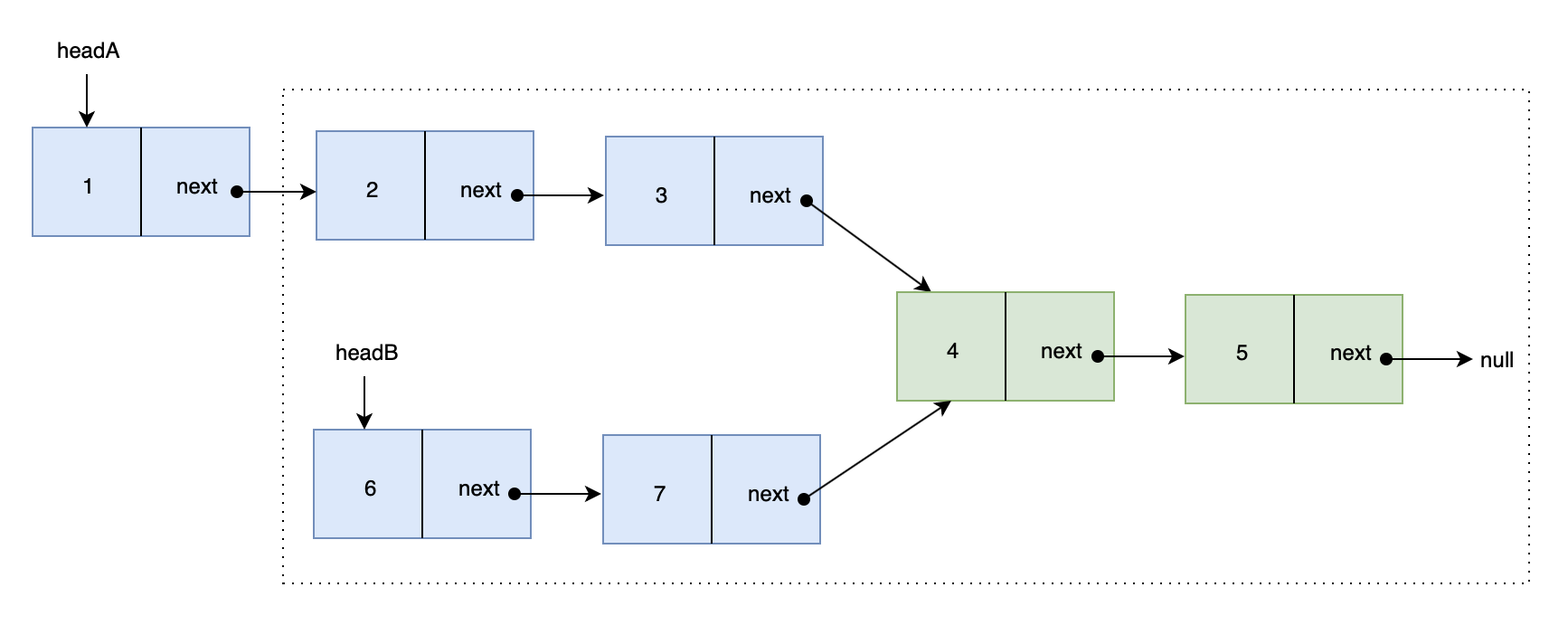
我们可以尝试消除 A、B 链表的长度差，同步遍历上图中的方框里的节点，判断是否有相同节点，若有相同则是两链表相交，返回第一个相同节点 即可。否则返回 null ，两链表不相交。

解题步骤：

• 同步遍历 A、B 链表 pA 、 pB ，直到遍历完其中一个链表（短链表），如上图，设A为长链表
• 那么此时 A、B 两遍表的长度差就为 pA 到链尾的长度，此时可以把 pB 指向长链表的表头 headA ，继续同步遍历，直到遍历完长链表
• 此时，headA 到 pB 的长度就为两链表的长度差，pB 到链表的长度与 headB 到链尾的长度一致
• 此时，可将 pA 指向 headB ，然后同步遍历 pB 及 pA ，直到有相交节点，返回相交节点，否则返回 null

画图帮助理解：

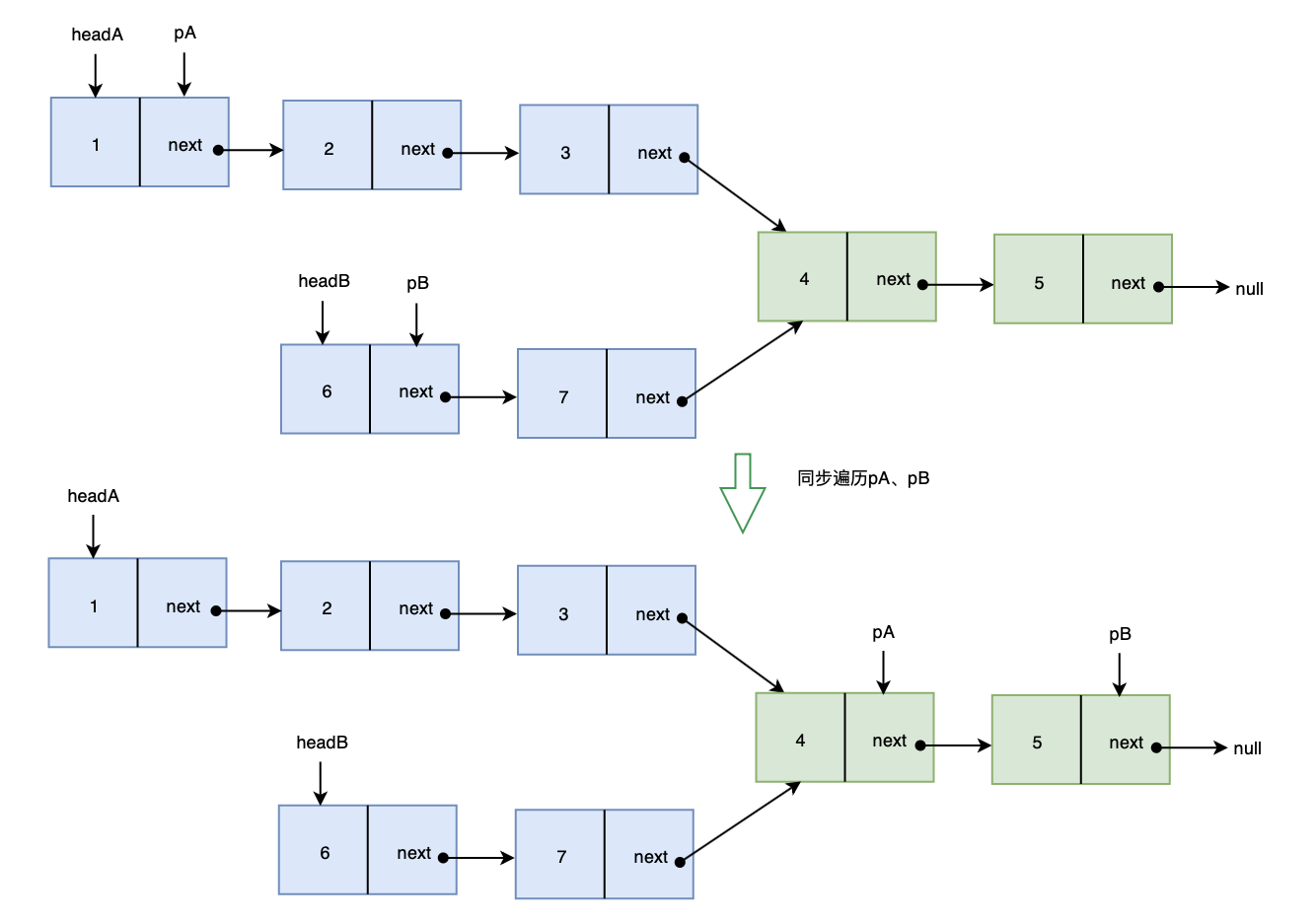
var getIntersectionNode = function(headA, headB) {
    // 清除高度差
    let pA = headA, pB = headB
    while(pA || pB) {
        if(pA === pB) return pA
        pA = pA === null ? headB : pA.next
        pB = pB === null ? headA : pB.next
    }
    return null
};

时间复杂度：O(n)

空间复杂度：O(1)

leetcode

3. 更多解法请看 图解字节&leetcode160：编写一个程序，找到两个单链表相交的起始节点

四、leetcode19：删除链表倒数第 n 个结点

1. 题目

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明：

给定的 n 保证是有效的。

进阶：

你能尝试使用一趟扫描实现吗？

2. 解法：快慢指针

解题思路： 需要删除链表中的倒数第 n 个节点，我们需要知道的就是倒数第 n+1 个节点，然后删除删除倒数第 n+1 节点的后继节点即可

步骤：

使用 2 个指针：

• fast 快指针提前走 n+1 步
• slow 指针指向当前距离 fast 倒数第 n 个节点， 初始为 head

然后， fast 、 slow 同步向前走，直到 fast.next 为 null

此时，fast 为最后一个节点，slow 就是倒数第 n+1 个节点，此时问题就变更为删除链表中的 slow 的后继节点

但存在一个问题，当链表长度为 n 时，fast 是前进不到 n+1 个节点位置的，所以此时有两种解决思路：

• 创建一个头节点 preHead ，设置 preHead.next = head ，这样就可以解决以上问题，删除倒数第 n 个节点后，返回的 preHead.next 即可
• 另外一种是，fast 快指针提前走 n 步后，判断 fast.next 是否为 null ，即 fast 是否是最后一个节点，如果是，则 head 为倒数第 n 个节点，此时问题可以简化为删除头节点；如果不是， fast = fast.next ，fast 再前进一步，slow 为倒数第 n+1 个节点，也解决了以上问题。

解决方案一：添加 preHead 节点

var removeNthFromEnd = function(head, n) {
    let preHead = new ListNode(0)
    preHead.next = head
    let fast = preHead, slow = preHead
    // 快先走 n+1 步
    while(n--) {
        fast = fast.next
    }
    // fast、slow 一起前进
    while(fast && fast.next) {
        fast = fast.next
        slow = slow.next
    }
    slow.next = slow.next.next
    return preHead.next
};

解决方案二：单独处理倒数第 n 节点

var removeNthFromEnd = function(head, n) {
    let fast = head, slow = head
    // 快先走 n 步
    while(--n) {
        fast = fast.next
    }
    if(!fast.next) return head.next
    fast = fast.next
    // fast、slow 一起前进
    while(fast && fast.next) {
        fast = fast.next
        slow = slow.next
    }
    slow.next = slow.next.next
    return head
};

时间复杂度：O(n)

空间复杂度：O(1)

leetcode

3. 更多解法请看 leetcode19：删除链表倒数第 n 个结点

五、leetcode876：求链表的中间结点

1. 题目

给定一个带有头结点 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。

注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.

示例 2：

输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])

由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。

提示：

给定链表的结点数介于 1 和 100 之间。

2. 解法：快慢指针

解题思路： 快指针一次走两步，慢指针一次走一步，当快指针走到终点时，慢指针刚好走到中间

var middleNode = function(head) {
    let fast = head, slow = head
    while(fast && fast.next) {
        slow = slow.next
        fast = fast.next.next
    }
    return slow
};

时间复杂度：O(n)

空间复杂度：O(1)

leetcode

3. 更多解法请看 leetcode876：求链表的中间结点

六、图解leetcode206：反转链表

1. 题目

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

进阶: 你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

2. 答案

解法一：迭代法

解题思路： 将单链表中的每个节点的后继指针指向它的前驱节点即可

画图实现： 画图帮助理解一下

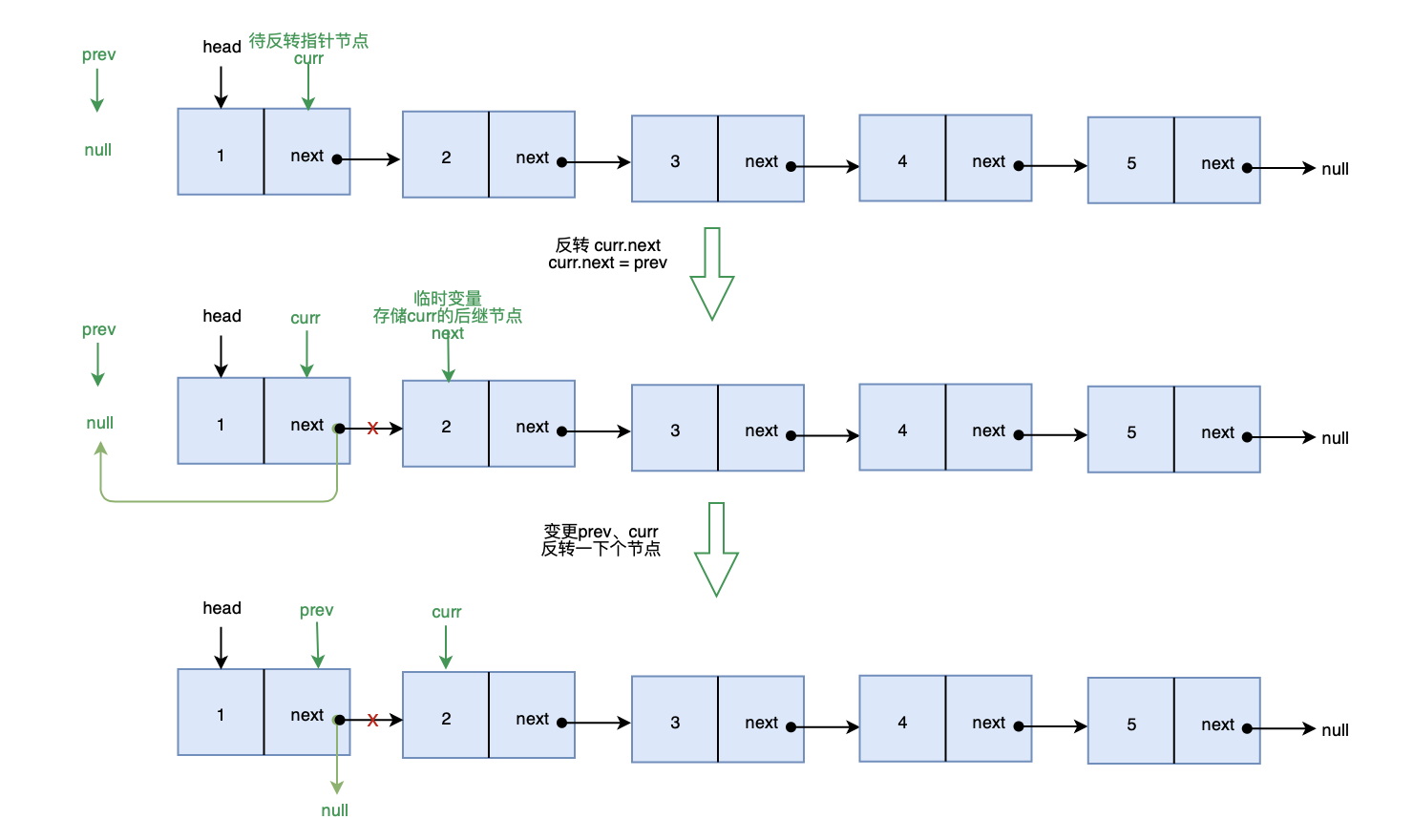
确定边界条件： 当链表为 null 或链表中仅有一个节点时，不需要反转

代码实现：

var reverseList = function(head) {
    if(!head || !head.next) return head
    var prev = null, curr = head
    while(curr) {
        // 用于临时存储 curr 后继节点
        var next = curr.next
        // 反转 curr 的后继指针
        curr.next = prev
        // 变更prev、curr 
        // 待反转节点指向下一个节点 
        prev = curr
        curr = next
    }
    head = prev
    return head
};

时间复杂度：O(n)

空间复杂度：O(1)

解法二：尾递归法

解题思路： 从头节点开始，递归反转它的每一个节点，直到 null ，思路和解法一类似

代码实现：

var reverseList = function(head) {
    if(!head || !head.next) return head
    head = reverse(null, head)
    return head
};

var reverse = function(prev, curr) {
    if(!curr) return prev
    var next = curr.next
    curr.next = prev
    return reverse(curr, next)
};

时间复杂度：O(n)

空间复杂度：O(n)

解法三：递归法

解题思路： 不断递归反转当前节点 head 的后继节点 next

画图实现： 画图帮助理解一下

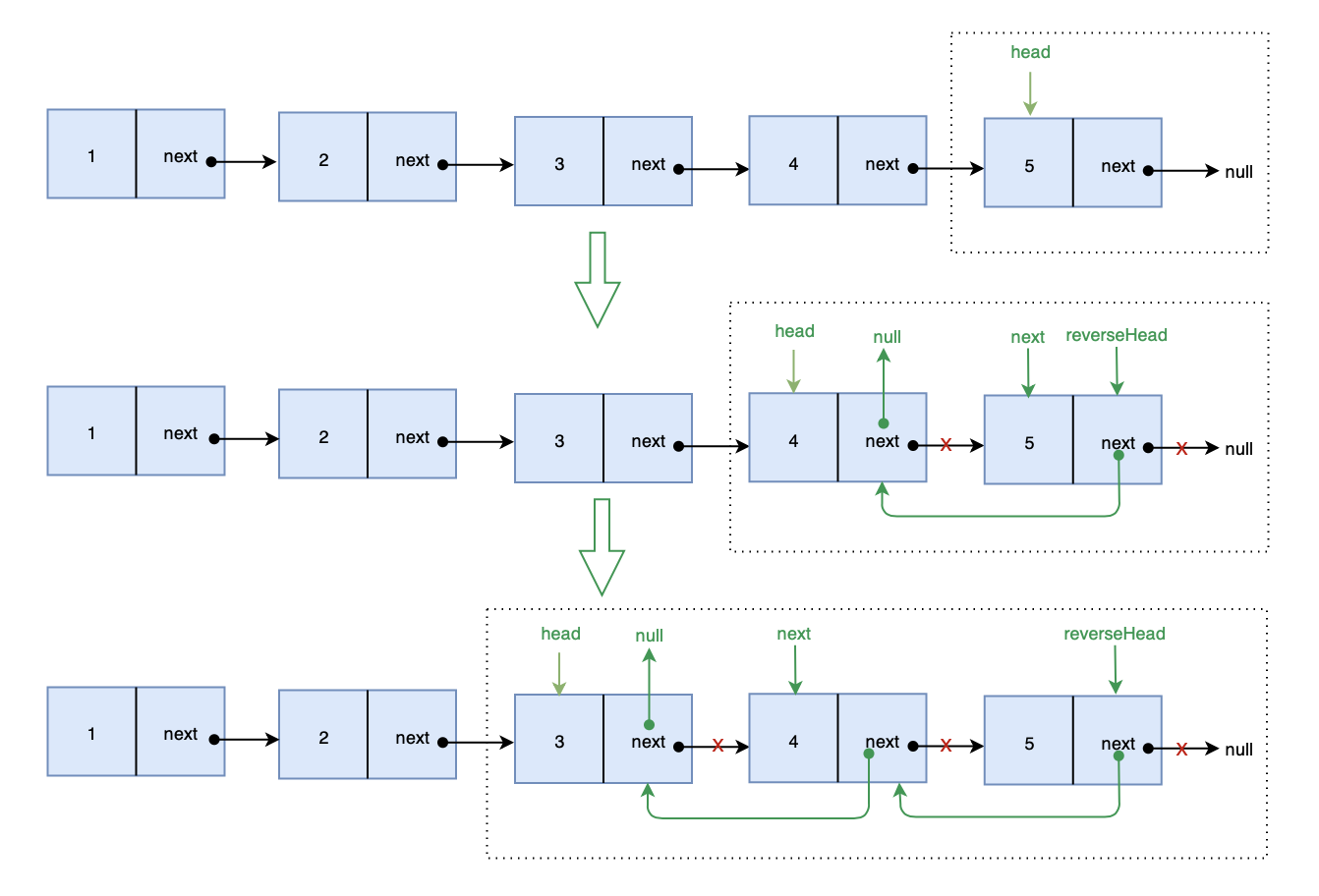
代码实现：

var reverseList = function(head) {
    if(!head || !head.next) return head
    var next = head.next
    // 递归反转
    var reverseHead = reverseList(next)
    // 变更指针
    next.next = head
    head.next = null
    return reverseHead
};

时间复杂度：O(n)

空间复杂度：O(n)

leetcode

3. 更多解法请看 leetcode206：反转链表

七、前端算法集训营第一期免费加入啦

引言

栈结构很简单，我们可以通过数组就能模拟出一个栈结构，但仅仅介绍栈结构就太不前端了，本节从栈结构开始延伸到浏览器中 JavaScript 运行机制，还有存储机制上用到的栈结构及相关数据结构，一文吃透所有的前端栈知识。

以后再提到栈时，我们不再仅限于 LIFO 了，而是一个有深度的栈。

这部分是前端进阶资深必备，如果你想打造高性能的前端应用，也需要了解这块，同时它也是面试的常见考察点。

理解栈对于我们理解 JavaScript 语言至关重要，本文主要从以下几个方面介绍栈：

• 首先介绍栈及代码实现
• 介绍 JavaScript 运行机制及栈在其中的应用
• 详细介绍调用栈及我们开发中如何利用调用栈
• JS 内存机制：栈（基本类型、引用类型地址）与堆（引用类型数据）
• 最后来一份总结与字节&leetcode刷题，实现最小栈

本节吃透栈原理，之后几天会每日一题，刷透栈题目，下面进入正文吧👍

一、 栈

栈是一种遵从后进先出 (LIFO / Last In First Out) 原则的有序集合，它的结构类似如下：

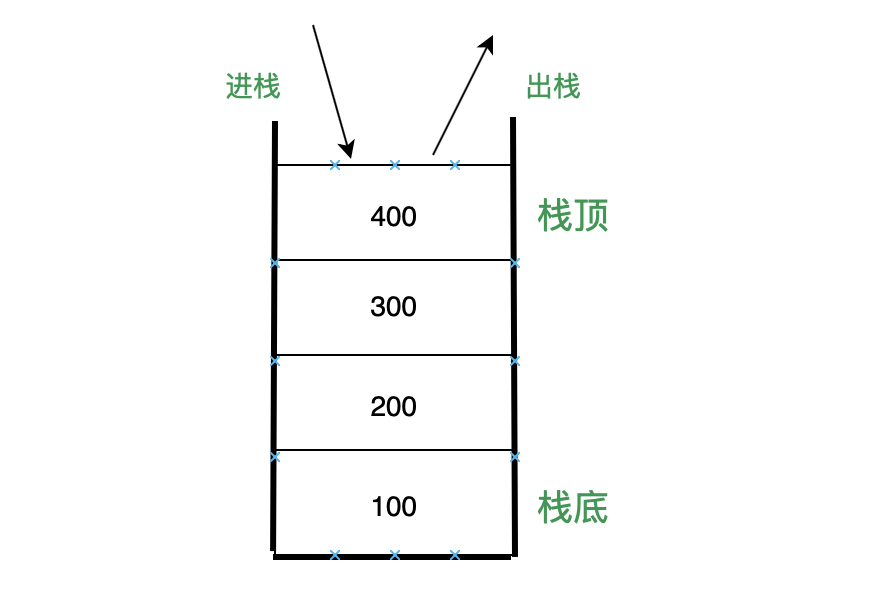
栈的操作主要有： push(e) (进栈)、 pop() (出栈)、 isEmpty() (判断是否是空栈)、 size() (栈大小)，以及 clear() 清空栈，具体实现也很简单。

二、代码实现

function Stack() {
  let items = []
  this.push = function(e) { 
    items.push(e) 
  }
  this.pop = function() { 
    return items.pop() 
  }
  this.isEmpty = function() { 
    return items.length === 0 
  }
  this.size = function() { 
    return items.length 
  }
  this.clear = function() { 
    items = [] 
  }
}

查找：从栈头开始查找，时间复杂度为 O(n)

插入或删除：进栈与出栈的时间复杂度为 O(1)

三、浏览器中 JS 运行机制

我们知道 JavaScript 是单线程的，所谓单线程，是指在 JavaScript 引擎中负责解释和执行 JavaScript 代码的线程唯一，同一时间上只能执行一件任务。

为什么是单线程的喃？这是因为 JavaScript 可以修改 DOM 结构，如果 JavaScript 引擎线程不是单线程的，那么可以同时执行多段 JavaScript，如果这多段 JavaScript 都修改 DOM，那么就会出现 DOM 冲突。

为了避免 DOM 渲染的冲突，可以采用单线程或者死锁，JavaScript 采用了单线程方案。

但单线程有一个问题：如果任务队列里有一个任务耗时很长，导致这个任务后面的任务一直排队等待，就会发生页面卡死，严重影响用户体验。

为了解决这个问题，JavaScript 将任务的执行模式分为两种：同步和异步。

同步

// 同步任务
let a = 1
console.log(a) // 1

异步

// 异步任务
setTimeout(() => {
    console.log('时间到')
}, 1000)

同步任务都在主线程（这里的主线程就是 JavaScript 引擎线程）上执行，会形成一个 调用栈 ，又称 **执行栈 **；

除了主线程外，还有一个任务队列（也称消息队列），用于管理异步任务的 事件回调 ，在 调用栈 的任务执行完毕之后，系统会检查任务队列，看是否有可以执行的异步任务。

注意：任务队列存放的是异步任务的事件回调

例如上例：

setTimeout(() => {
    console.log('时间到')
}, 1000)

在执行这段代码时，并不会立刻打印 ，只有定时结束后（1s）才打印。 setTimeout 本身是同步执行的，放入任务队列的是它的回调函数。

下面我们重点看一下主线程上的调用栈。

四、调用栈

我们从以下两个方面介绍调用栈：

• 调用栈的用来做什么
• 在开发中，如何利用调用栈

1. 调用栈的职责

我们知道，在 JavaScript 中有很多函数，经常会出现一个函数调用另外一个函数的情况，调用栈就是用来管理函数调用关系的一种栈结构 。

那么它是如何去管理函数调用关系喃？我们举例说明：

var a = 1
function add(a) {
  var b = 2
  let c = 3
  return a + b + c
}

// 函数调用
add(a)

这段代码很简单，就是创建了一个 add 函数，然后调用了它。

下面我们就一步步的介绍整个函数调用执行的过程。

在执行这段代码之前，JavaScript 引擎会先创建一个全局执行上下文，包含所有已声明的函数与变量：

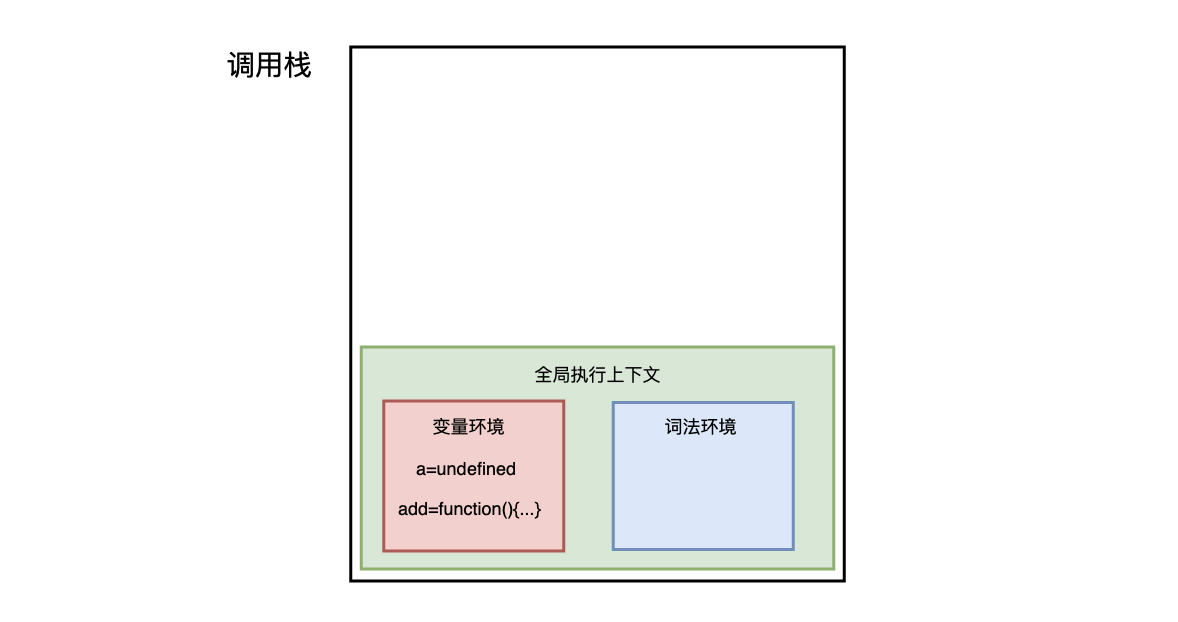
从图中可以看出，代码中的全局变量 a 及函数 add 保存在变量环境中。

执行上下文准备好后，开始执行全局代码，首先执行 a = 1 的赋值操作，

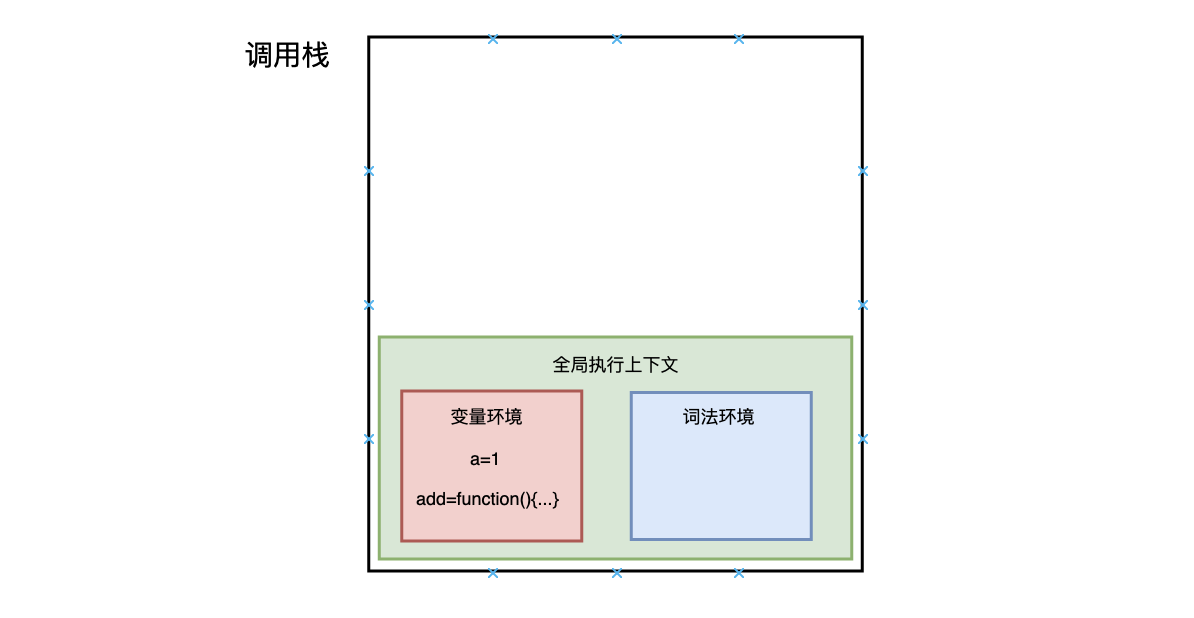
赋值完成后 a 的值由 undefined 变为 1，然后执行 add 函数，JavaScript 判断出这是一个函数调用，然后执行以下操作：

• 首先，从全局执行上下文中，取出 add 函数代码
• 其次，对 add 函数的这段代码进行编译，并创建该函数的执行上下文和可执行代码，并将执行上下文压入栈中

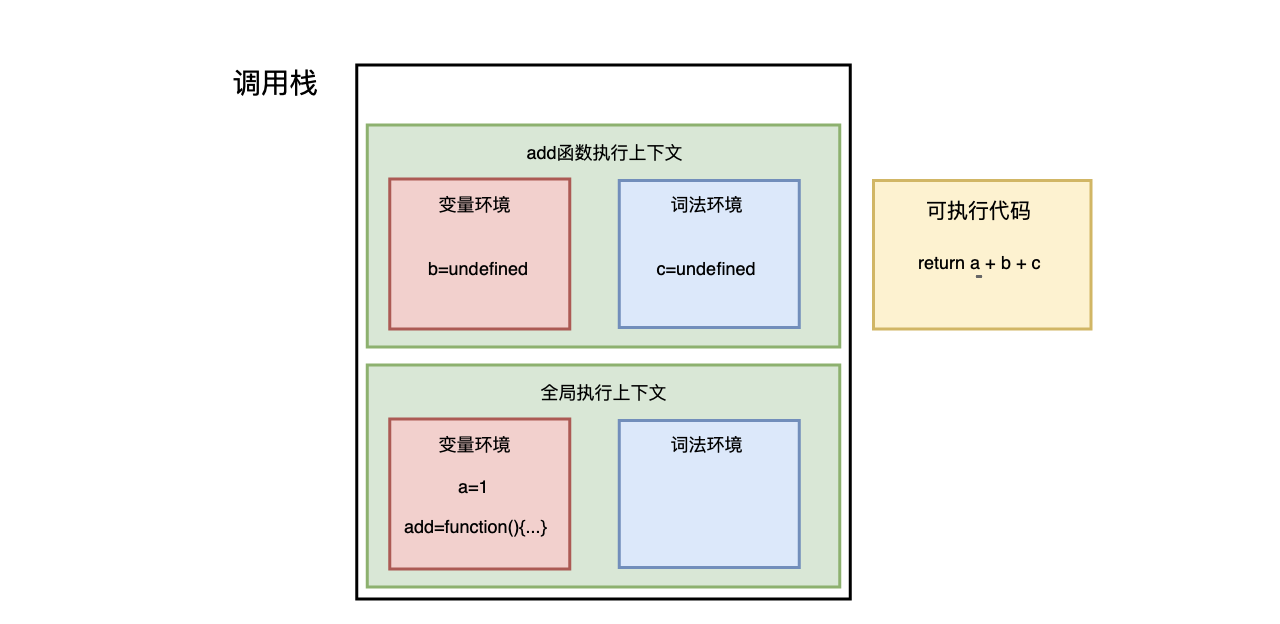
• 然后，执行代码，返回结果，并将 add 的执行上下文也会从栈顶部弹出，此时调用栈中就只剩下全局上下文了。

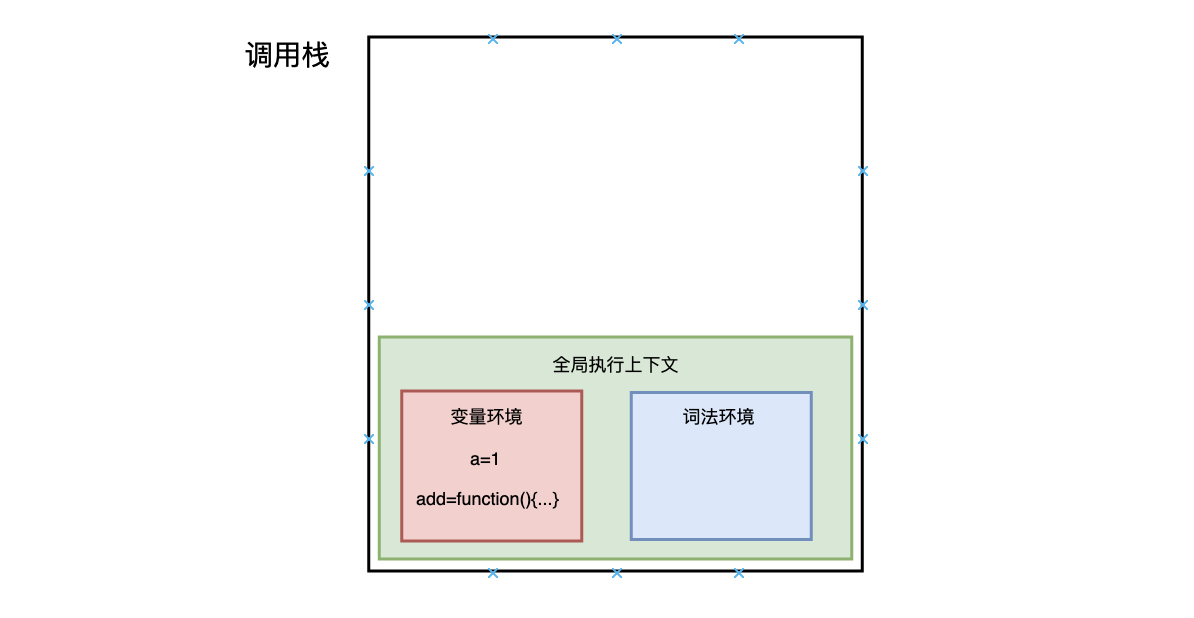
至此，整个函数调用执行结束了。

所以说，调用栈是 JavaScript 用来管理函数执行上下文的一种数据结构，它记录了当前函数执行的位置，哪个函数正在被执行。 如果我们执行一个函数，就会为函数创建执行上下文并放入栈顶。 如果我们从函数返回，就将它的执行上下文从栈顶弹出。 也可以说调用栈是用来管理这种执行上下文的栈，或称执行上下文栈（执行栈）。

2. 懂调用栈的开发人员有哪些优势

栈溢出

在我们执行 JavaScript 代码的时候，有时会出现栈溢出的情况：

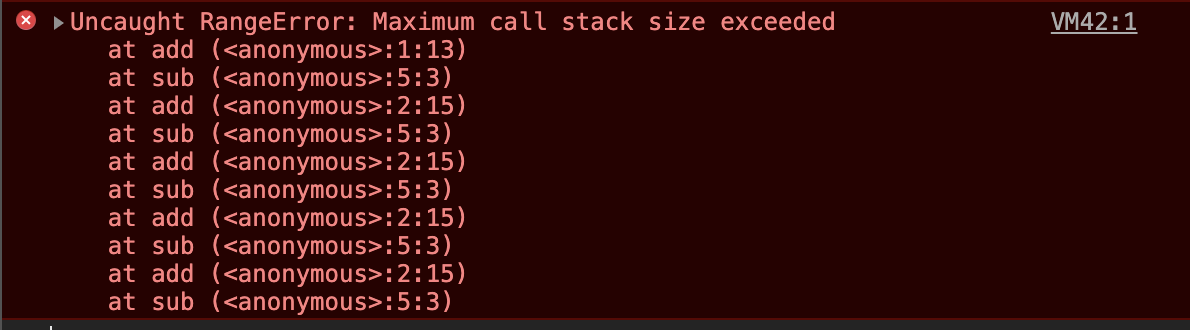
上图就是一个典型的栈溢出，那为什么会出现这种错误喃？

我们知道调用栈是用来管理执行上下文的一种数据结构，它是有大小的，当入栈的上下文过多的时候，它就会报栈溢出，例如：

function add() {
  return 1 + add()
}

add()

add 函数不断的递归，不断的入栈，调用栈的容量有限，它就溢出了，所以，我们日常的开发中，一定要注意此类代码的出现。

在浏览器中获取调用栈信息

两种方式，一种是断点调试，这种很简单，我们日常开发中都用过。

一种是 console.trace()

function sum(){
  return add()
}
function add() {
  console.trace()
  return 1
}

// 函数调用
sum()

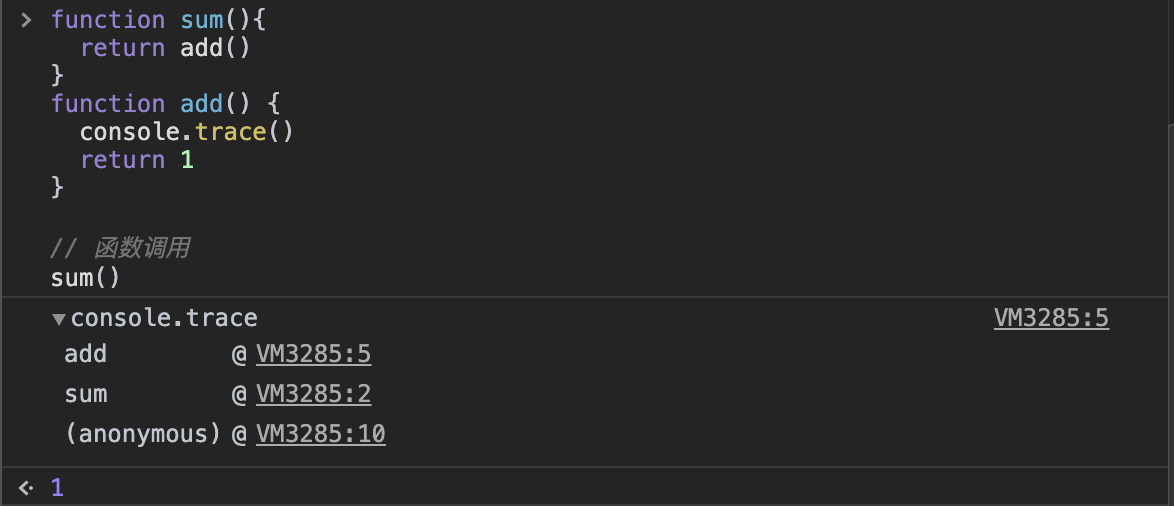
五、JS 内存机制：栈（基本类型、引言类型地址）与堆（引用类型数据）

在 JavaScript 开发日常中，前端人员很少有机会了解内存，但如果你想成为前端的专家，打造高性能的前端应用，你就需要了解这一块，同时它也是面试的常见考察点。

JavaScript 中的内存空间主要分为三种类型：

• 代码空间：主要用来存放可执行代码
• 栈空间：调用栈的存储空间就是栈空间。
• 堆空间

代码空间主要用来存放可执行代码的。栈空间及堆空间主要用来存放数据的。接下来我们主要介绍栈空间及堆空间。

JavaScript 中的变量类型有 8 种，可分为两种：基本类型、引用类型

基本类型：

• undefined
• null
• boolean
• number
• string
• bigint
• symbol

引用类型：

• object

其中，基本类型是保存在栈内存中的简单数据段，而引用类型保存在堆内存中。

1. 栈空间

基本类型在内存中占有固定大小的空间，所以它们的值保存在栈空间，我们通过 按值访问 。

一般栈空间不会很大。

2. 堆空间

引用类型，值大小不固定，但指向值的指针大小（内存地址）是固定的，所以把对象放入堆中，将对象的地址放入栈中，这样，在调用栈中切换上下文时，只需要将指针下移到上个执行上下文的地址就可以了，同时保证了栈空间不会很大。

当查询引用类型的变量时， 先从栈中读取内存地址， 然后再通过地址找到堆中的值。对于这种，我们把它叫做 按引用访问 。

一般堆内存空间很大，能存放很多数据，但它内存分配与回收都需要花费一定的时间。

举个例子帮助理解一下：

var a = 1
function foo() {
  var b = 2
  var c = { name: 'an' }
}

// 函数调用
foo()

基本类型（栈空间）与引用类型（堆空间）的存储方式决定了：基本类型赋值是值赋值，而引用类型赋值是地址赋值。

// 值赋值
var a = 1
var b = a
a = 2
console.log(b) 
// 1
// b 不变

// 地址赋值
var a1 = {name: 'an'}
var b1 = a1
a1.name = 'bottle'
console.log(b1)
// {name: "bottle"}
// b1 值改变

3. 垃圾回收

JavaScript 中的垃圾数据都是由垃圾回收器自动回收的，不需要手动释放。所以大部分的开发人员并不了解垃圾回收，但这部分也是前端进阶资深必备！

回收栈空间

在 JavaScript 执行代码时，主线程上会存在 ESP 指针，用来指向调用栈中当前正在执行的上下文，如下图，当前正在执行 foo 函数：

当 foo 函数执行完成后，ESP 向下指向全局执行上下文，此时需要销毁 foo 函数。

怎么销毁喃？

当 ESP 指针指向全局执行上下文，foo 函数执行上下文已经是无效的了，当有新的执行上下文进来时，可以直接覆盖这块内存空间。

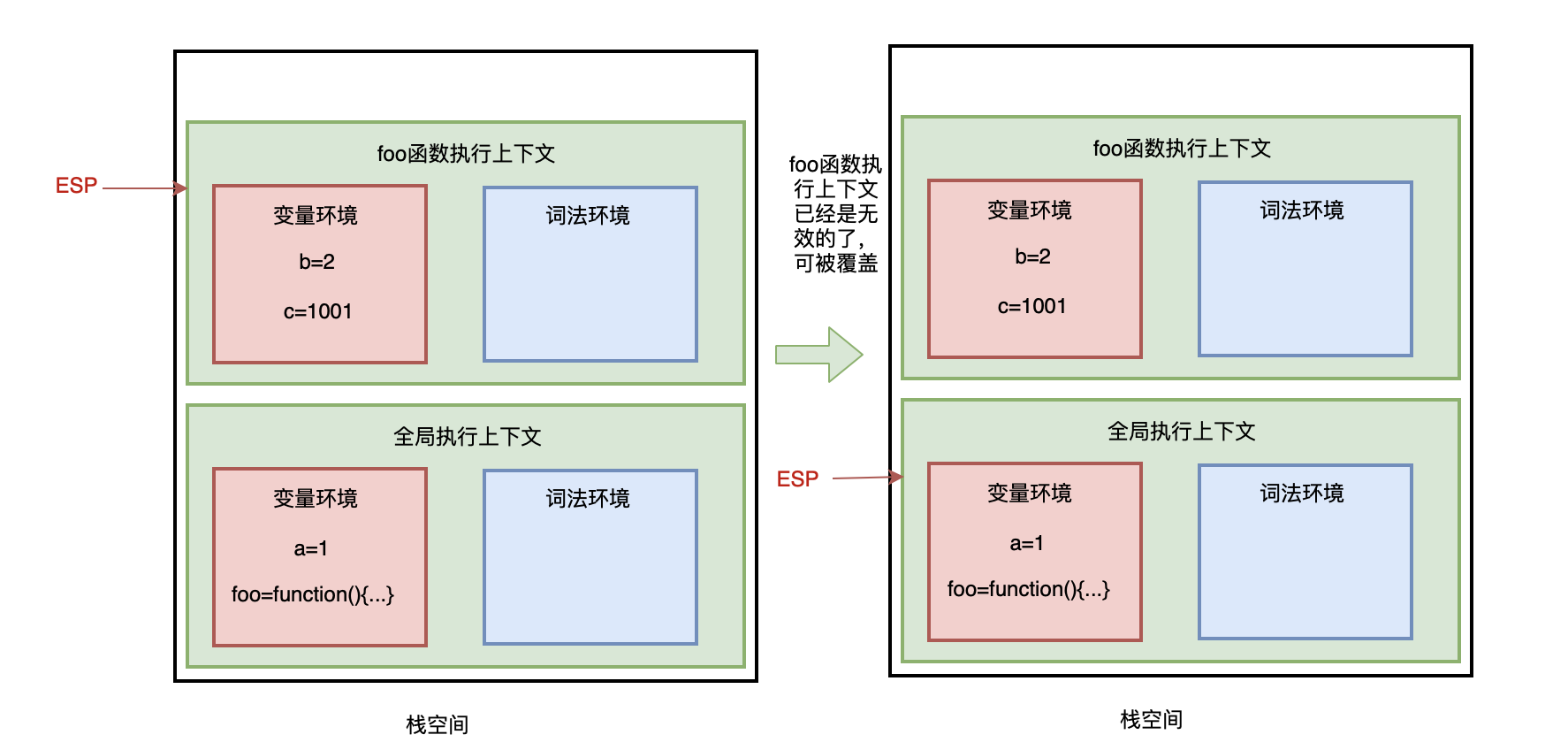
即：JavaScript 引擎通过向下移动 ESP 指针来销毁存放在栈空间中的执行上下文。

回收堆空间

V8 中把堆分成新生代与老生代两个区域：

• 新生代：用来存放生存周期较短的小对象，一般只支持1～8M的容量
• 老生代：用来存放生存周期较长的对象或大对象

V8 对这两块使用了不同的回收器：

• 新生代使用副垃圾回收器
• 老生代使用主垃圾回收器

其实无论哪种垃圾回收器，都采用了同样的流程（三步走）：

• 标记： 标记堆空间中的活动对象（正在使用）与非活动对象（可回收）
• 垃圾清理： 回收非活动对象所占用的内存空间
• 内存整理： 当进行频繁的垃圾回收时，内存中可能存在大量不连续的内存碎片，当需要分配一个需要占用较大连续内存空间的对象时，可能存在内存不足的现象，所以，这时就需要整理这些内存碎片。

副垃圾回收器与主垃圾回收器虽然都采用同样的流程，但使用的回收策略与算法是不同的。

副垃圾回收器

它采用 Scavenge 算法及对象晋升策略来进行垃圾回收

所谓 Scavenge 算法，即把新生代空间对半划分为两个区域，一半是对象区域，一半是空闲区域，如下图所示：

新加入的对象都加入对象区域，当对象区满的时候，就执行一次垃圾回收，执行流程如下：

• 标记：首先要对区域内的对象进行标记（活动对象、非活动对象）
• 垃圾清理：然后进行垃圾清理：将对象区的活动对象复制到空闲区域，并进行有序的排列，当复制完成后，对象区域与空闲区域进行翻转，空闲区域晋升为对象区域，对象区域为空闲区域

翻转后，对象区域是没有碎片的，此时不需要进行第三步（内存整理了）

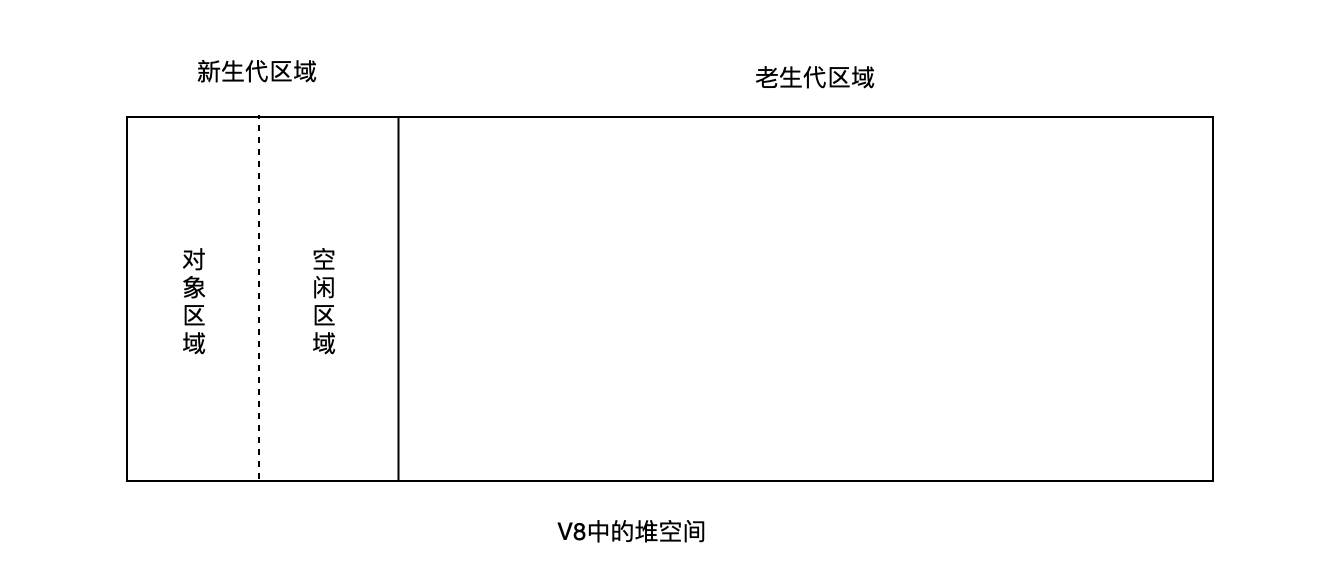
但，新生代区域很小的，一般1～8M的容量，所以它很容易满，所以，JavaScript 引擎采用对象晋升策略来处理，即只要对象经过两次垃圾回收之后依然继续存活，就会被晋升到老生代区域中。

主垃圾回收器

老生代区域里除了存在从新生代晋升来的存活时间久的对象，当遇到大对象时，大对象也会直接分配到老生代。

所以主垃圾回收器主要保存存活久的或占用空间大的对象，此时采用 Scavenge 算法就不合适了。V8 中主垃圾回收器主要采用标记-清除法进行垃圾回收。

主要流程如下：

• 标记：遍历调用栈，看老生代区域堆中的对象是否被引用，被引用的对象标记为活动对象，没有被引用的对象（待清理）标记为垃圾数据。
• 垃圾清理：将所有垃圾数据清理掉
• 内存整理：标记-整理策略，将活动对象整理到一起

增量标记

V8 浏览器会自动执行垃圾回收，但由于 JavaScript 也是运行在主线程上的，一旦执行垃圾回收，就要打断 JavaScript 的运行，可能会或多或少的造成页面的卡顿，影响用户体验，所以 V8 决定采用增量 标记算法回收：

即把垃圾回收拆成一个个小任务，穿插在 JavaScript 中执行。

六、总结

本节从栈结构开始介绍，满足后进先出 (LIFO) 原则的有序集合，然后通过数组实现了一个栈。

接着介绍浏览器环境下 JavaScript 的异步执行机制，即事件循环机制， JavaScript 主线程不断的循环往复的从任务队列中读取任务（异步事件回调），放入调用栈中执行。调用栈又称执行上下文栈（执行栈），是用来管理函数执行上下文的栈结构。

JavaScript 的存储机制分为代码空间、栈空间以及堆空间，代码空间用于存放可执行代码，栈空间用于存放基本类型数据和引用类型地址，堆空间用于存放引用类型数据，当调用栈中执行完成一个执行上下文时，需要进行垃圾回收该上下文以及相关数据空间，存放在栈空间上的数据通过 ESP 指针来回收，存放在堆空间的数据通过副垃圾回收器（新生代）与主垃圾回收器（老生代）来回收。

聊聊就跑远了🤦‍♀️，但都是前端进阶必会，接下来我们开始刷栈题目吧！！！每日一刷，进阶前端与算法⛽️⛽️⛽️，来道简单的吧！

七、字节&leetcode155：最小栈（包含getMin函数的栈）

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) —— 将元素 x 推入栈中。
• pop() —— 删除栈顶的元素。
• top() —— 获取栈顶元素。
• getMin() —— 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

欢迎将答案提交到 github.com/sisterAn/Ja…

八、参考资料

浏览器工作原理与实践（极客时间）

九、认识更多的前端道友，一起进阶前端开发

前端算法集训营第一期免费开营啦🎉🎉🎉，免费哟！

在这里，你可以和志同道合的前端朋友们（1000+）一起进阶前端算法，从0到1构建完整的数据结构与算法体系。

在这里，你可以每天学习一道大厂算法题（阿里、腾讯、百度、字节等等）或 leetcode，瓶子君都会在第二天解答哟！

扫码加入，若群人数已达上线，关注公众号「前端瓶子君」，回复「算法」即可自动加入