今天的LeetCode每日一题正好是可以用广度优先搜索来解题,下文先谈谈BFS解题套路技巧,然后分析LeetCode第542题 - 01矩阵
广度优先搜索(Breadth-First-Search, BFS)
广度优先遍历类似与二叉树的层序遍历。它是一种分层的查找过程,每向前走一步能访问一批顶点,不像深度优先遍历那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个先进先出队列,以记忆正在访问顶点的下一层顶点,如下图:
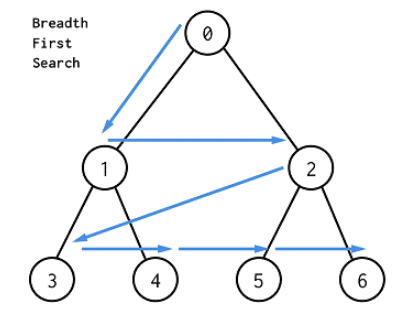
而深度搜索(Depth-First-Search, DFS) 则是往一条路走到底,直到走不通了,再回头搜索。它的遍历类似于树的先序遍历。DFS算法是一个递归的算法,需要借助一个递归的工作栈,如下图:
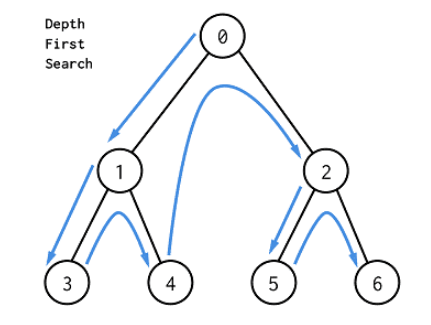
如果从路径上走来看,DFS就是一条跑的很快的疯狗,到处乱咬。没路了就转头,再没路了再跑回来去其他地方,而BFS就像是一团毒气,慢慢延申!
BFS解题模板
BFS使用队列,把每个还没有搜索到的点依次放入队列,然后再弹出队列的头部元素当做当前遍历点,经典通用模板:
while(!queue.isEmpty()) {
cur = queue.pop() // 取出头部元素进行搜索
for (节点 in : cur的所有相邻节点) {
if (该节点有效,并且未访问过) {
标记该节点已被访问;
// 赋值等处理...
queue.offer(该节点); // 把此节点添加到队列尾部
}
}
}
此模板是BFS通用解题模板,任何题目都是可以套用的。
01矩阵题

分析题目
为0的位置距离就是0,不用我们计算。关键点就在1,要找出每个1到0的最近曼哈顿距离(元素只在四个方向相邻:上、下、左、右)。由于1到0的距离和0到1的距离是相等的,所以我们换个思维:找出每个0到1的距离。
因此,此题可以抽象成,多个起始点的BFS,很简单,就是先遍历一遍矩阵,把所有值为0的先放入队列中,然后利用以上模板。
具体思路就是:首先把矩阵每个点 0 入队列( 0 值所在矩阵的下标),然后从各个 0 同时开始一圈一圈的向 1 扩散,扩散的时候可以设置 int[][] dist 来记录距离(即扩散的层次)并同时标志是否访问过。对于本题是可以直接修改原数组 int[][] matrix 来记录距离和标志是否访问的,这里要注意先把 matrix 数组中 1 的位置设置成 -1 (或者10000也行,只要是个无效的距离值来标志这个位置的 1 没有被访问过就可以)
复杂度分析
- 每个点入队出队一次,所以时间复杂度:O(m*n)
- 虽然我们是直接原地修改的原输入数组来存储结果,但最差的情况下即全都是 0 时,需要把 m*n个 0 都入队,因此空间复杂度是 O(m*n)
直接套用上面的模板解题,代码如下:
public int[][] updateMatrix(int[][] matrix) {
// 首先将所有的0先入队列,并将1的位置设置成-1,表示未被访问过的(因为只有0,1两个值,直接在元矩阵上修改)
Queue<int[]> queue = new LinkedList();
int m = matrix.length, n = matrix[0].length;
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
if (matrix[i][j] == 0) {
queue.offer(new int[]{i,j});
} else {
matrix[i][j] = -1;
}
}
}
// 向四个方向广搜
int[][] d = {{-1,0},{1,0},{0,-1},{0,1}}; //左右上下
while(!queue.isEmpty()) {
int[] point = queue.poll(); // 取出头部元素进行搜索
int i = point[0], j = point[1];
// 四个方向上找
for (int k=0; k<4; k++) {
int di = i + d[k][0];
int dj = j + d[k][1];
if (di >= 0 && di < m && dj >= 0 && dj < n && matrix[di][dj] == -1) {
// 找到未访问过的点,这个点到 0 的距离就可以更新为 matrix[x][y] + 1
matrix[di][dj] = matrix[i][j] + 1; // 赋值操作,同时标记成已被访问过
queue.offer(new int[]{di, dj}); // 把此节点添加到队列尾部
}
}
}
return matrix;
}