一、栈和队列

• 队列：先进先出
• 栈：先进后出

栈：开辟一块连续的存储空间

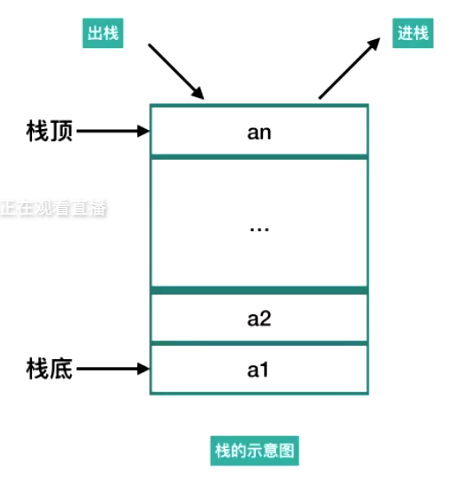
栈的顺序存储 链式存储

限定性数据结构 - 栈与队列的特点

顺序栈实现

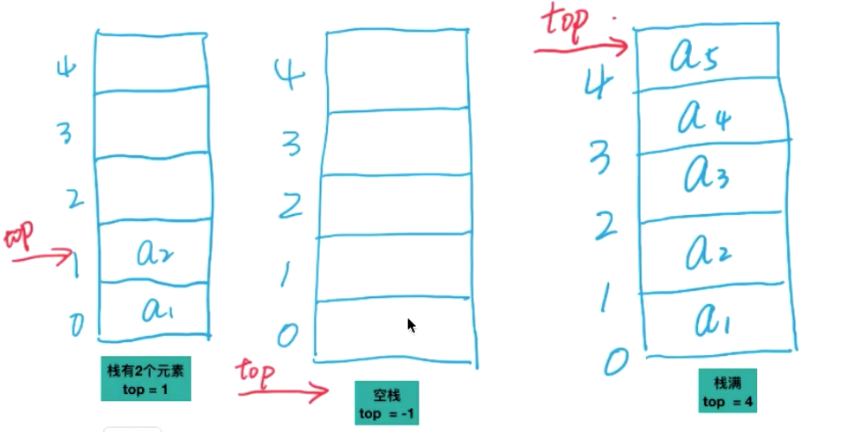
//定义栈的数据结构
#define MAXSIZE 20
typedef struct{ //SElemType类型根据实际情况而定，这里假设为int
    SElemType data[MAXSIZE];
    int top; //栈顶指针
}SqStack;

//构建一个空的栈
Status InitStack(SqStack *S){
    S->top = -1; //top指针为-1 表示空栈
    return OK;
}
//栈置空
Status ClearStack(SqStack *S){
    S->top = -1;
    return OK;
}
//判断栈是否为空
Status StackEmpty（SqStack S){
    if(S->top == -1)
        return TRUE;
    return FALSE;
}
//获取栈的长度
int StackLength(SqStack S){
    return S.top + 1;
}
//获取栈顶元素（不代表出栈）
Status GetTop(SqStack S,SElemType *e){
    if(S.top == -1){
        return ERROR;
    }
    *e = S.data[S.top];
    return OK;
}
//压栈（入栈）
Status PushData(SqStack *S,SElemType e){
    if(S->top == MAXSIZE -1 ) return ERROR; //判断是否满栈 
    S->top++;
    S->data[S->top] = e;
    return OK;
}
//出栈
Status PopData(SqStack *S,SElemType *e){
    if(S->top == -1) return ERROR;
    *e = S->data[S->top];
    S->top--;
    return OK;
}
//栈的遍历
Status StackTraverse(SqStack S){
    int i = 0;
    if(S.top == -1) return ERROR;
    
    printf("Stack Element:");
    while(i <= S.top){
        printf("%d",S.data[i++]);
    }
    printf("\n");
    return OK;
}

链式栈实现

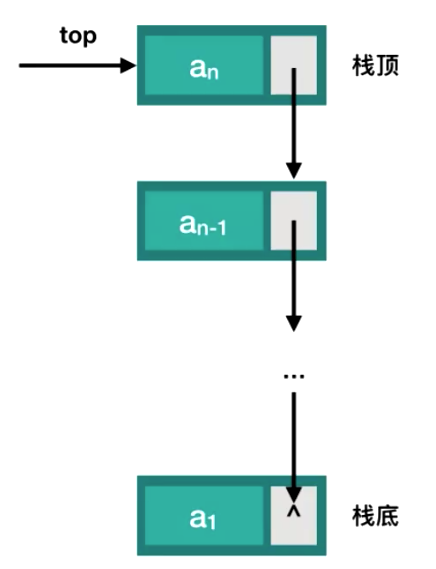
//设计栈的结点
typedef Struct StackNode{
    SElemType data;
    struct StackNode *next;
}StackNode,*LinkStackPtr;
//设计栈结构
typedef struct{
    LinkStactPtr top;
    int count;
}LinkStack;

//构建空栈
Status InitStack(LinkStack *S){
    S->top = (LinkStackPtr)malloc(sizeof(StackNode);
    if(S->top == NULL) return ERROR;
    S->top == NULL;
    S->count = 0;
    return OK;
    
}
//栈置空栈
Status ClearStack(LinkStack *S){
    LinkStackPtr p,q;
    p = S->top;
    while(p){
        q = p;
        p=q->next;
        free(q);
    }
    S->count = 0;
    return OK;
}
//判断栈是否为空
Status StackEmpty(LinkStack S){
    if(S.count == 0) return TRUE;
    return FALSE;
}
//栈的长调度
int StackLength(LinkStack S){
    return S.count;
}
//获取栈顶
Status GetTop(LinkStack S,SElmeType *e){
    if(S.top == NULL) return ERROR;
    *e = S.top->data;
    return OK;
}
//入栈
Status Push(LinkStack *S,SElemType e){
    LinkStackPtr temp = (LinkStackPtr)malloc(sizeof(StackNode));
    if(!temp) return ERROR;
    temp->data = e;
    temp->next = S->top;
    S->top = temp;
    S->count++;
    return OK;
}
//出栈
Status Pop(LinkStack *S,SElemType *e){
    if(StackEmpty(*S)) return ERROR;
    LinkStack p;
    *e = S->top->data;
    p = S->top;
    S->top = S->top->next;
    free(p);
    S->count--;
    return OK;
}
//栈的遍历
Status StackTraverse(LinkStack S){
    LinkStackPtr p;
    p = S.top;
    while(p){
        printf("%d",p->data);
        p = p->next;
    }
    return OK;
}

————————————————————

分割线

————————————————————

二、栈与递归

直接或间接调用自己本身就是递归 使用递归的条件

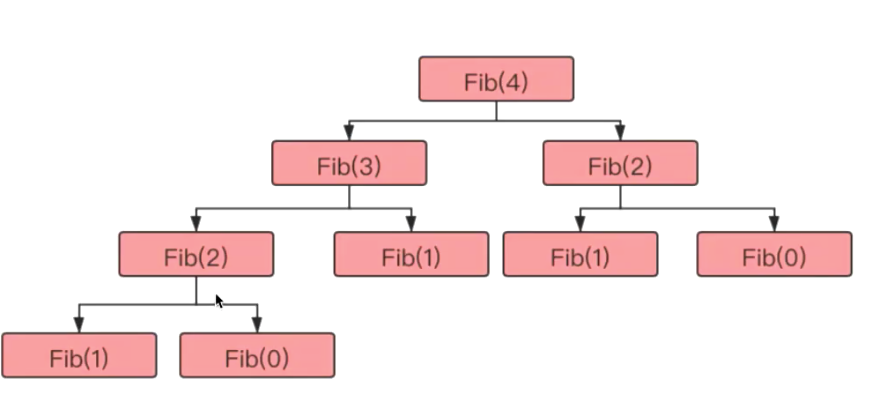
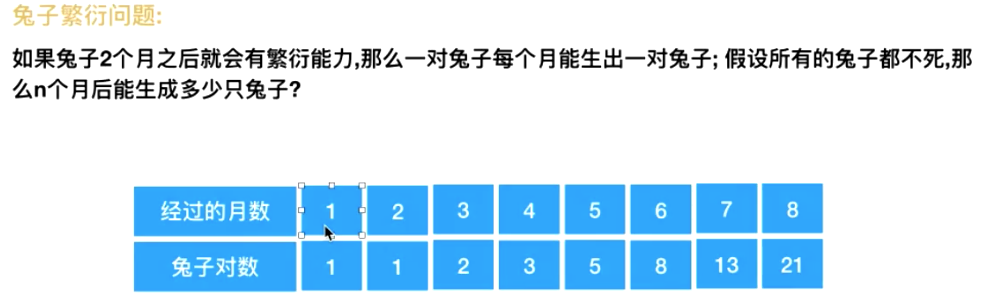
• 1.数学定义就是递归 如阶乘/斐波那契数列
• 2.数据结构是递归 链表的定义
• 3.问题是递归的 汉诺塔/八皇后

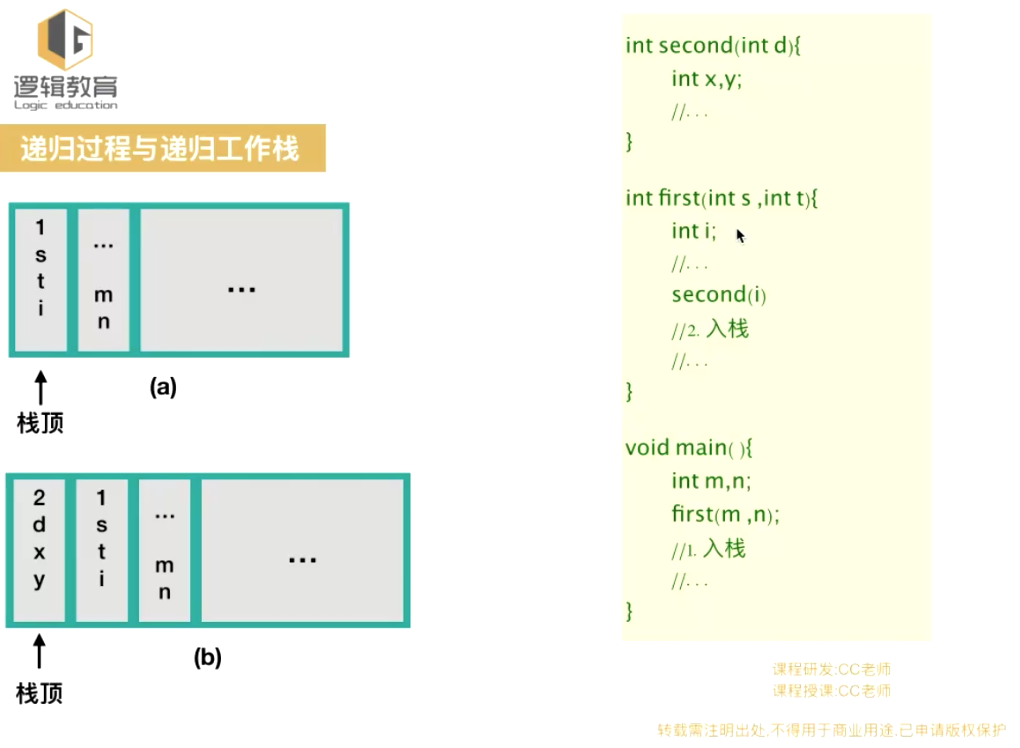
分治法：

• 1.条件高度重合，可以将问题拆分成高度相似的方法
• 2.通过分治可以简化问题
• 3.递归 要有出口 递归边界

//斐波那契数列
int Fbi(int i){
    if(i<2)
        return i==0?0:1;
    return Fbi(i-1)+Fbi(i-2);
}

————————————————————

分割线

————————————————————

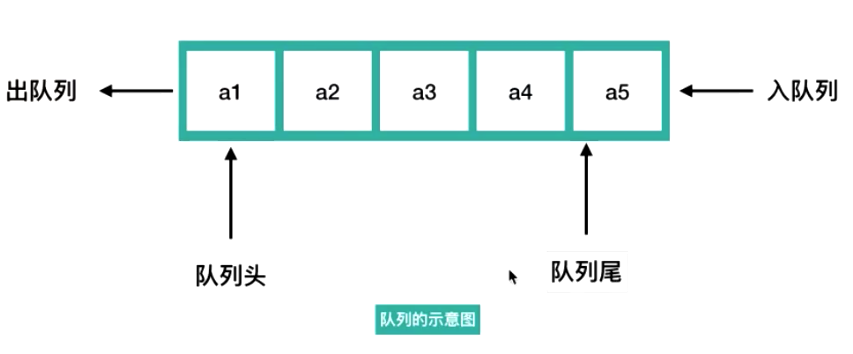
三、队列

从队尾插数据 从队头出数据

为了避免假溢出使用循环队列的情况

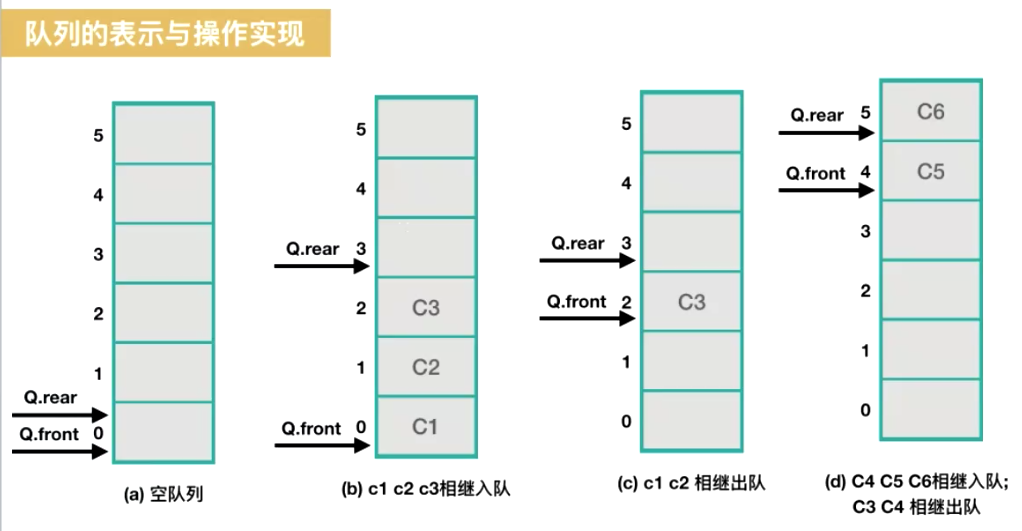
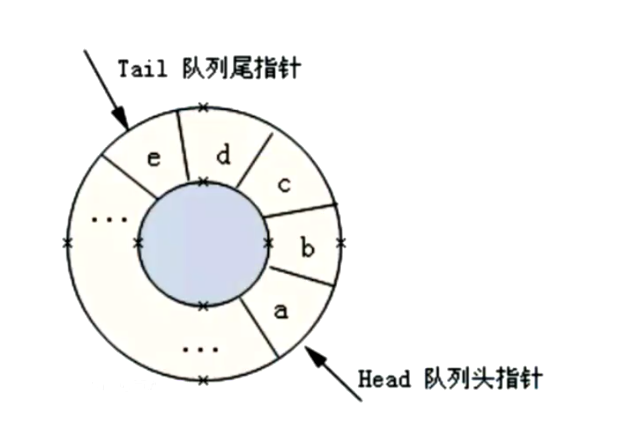
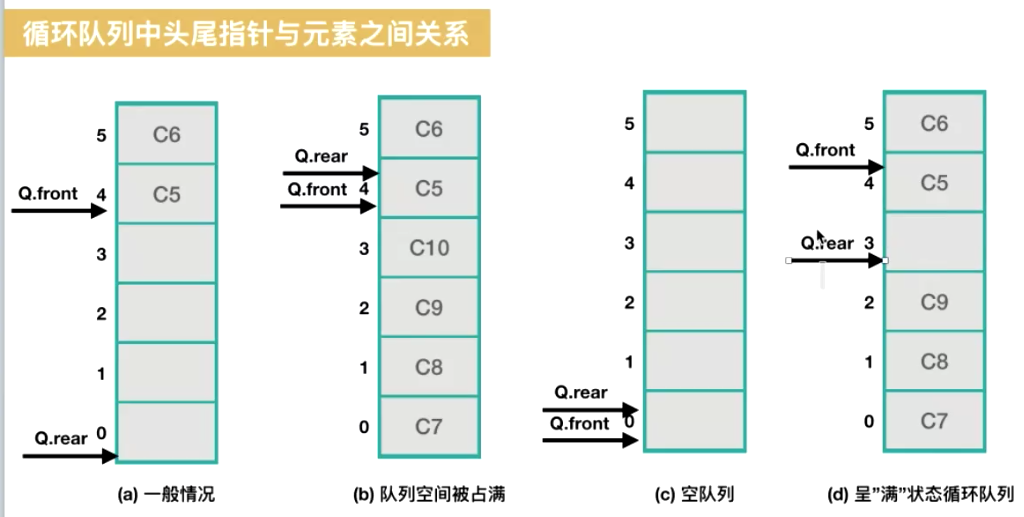
满状态下有一个留空（首尾不能相遇）

• 判断队空 Q.front == Q.rear;
• 判断队满 (Q.rear + 1) % MAXSIZE == Q.front

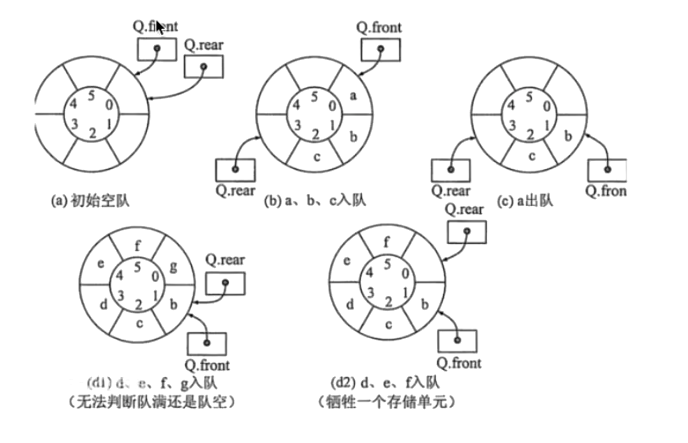
循环队列的操作实现

//数据结构
typedef struct{
    int rear;
    int front;
    SElemtype data[MAXSIZE];
}CqStack;

//
//  main.c
//  001--栈不同表示方式与实现
//
//  Created by CC老师 on 2019/9/21.
//  Copyright © 2019年 CC老师. All rights reserved.
//

#include "stdio.h"
#include "stdlib.h"

#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef int Status;
typedef int SElemType; /* SElemType类型根据实际情况而定，这里假设为int */

typedef struct{
    int rear;
    int front;
    SElemtype data[MAXSIZE];
}CqStack;

//初始化空队列
Status InitCqStack(CqStack *S){
    S->rear = 0;
    S->front = 0;
    return OK;
}
//清空
Status ClearCqStack(CqStack *S){
    S->rear = S->front = 0;
    return OK;
}

//判断为空
Status CqEmpty(CqStack *S){
    if(S.front == S.rear){
        return TRUE;
    }
    return FALSE;
}
//判断length
int CqLength(CqStack S){
    return (S.rear - S.front + MAXSIZE) % MAXSIZE;
}
//入队
Status pushCq(CqStack *S,SElemType *e){
    if((S->rear +1 ) % MAXSIZE == S->front ) return ERROR;
    S->data[S->rear] = e;
    S->rear = (S->rear +1) % MAXSIZE;
    return OK;
    
}
//出队
Status PopCq(CqStack *S,SElemType *e){
    if(S->front == S->rear) return ERROR;
    *e = S->data[S->front];
    S->front = (S->front +1) %MAXSIZE;
    return OK;
}
//遍历
Status CqTraverse(CqStack S){
    int i;
    i=S.front;
    printf("遍历循环队列\n");
    while(i!=S.rear){
        printf(S.data[i]);
        i = (i+1)%MAXSIZE;
    }
    printf("\n");
    return OK;
}
//获取头
Status getCqHead(CqStack S,SElemType *e){
    if(S.front == S.rear) return ERROR;
    
    *e = S.data[S.front];
    return OK;
}



int main(int argc, const char * argv[]) {
    // insert code here...
    printf("循环队列的表示与实现!\n");
    

    CqStack S;

    int e;
    
    if (InitCqStack(&S) == OK) {
        for (int j = 1 ; j < 10; j++) {
            pushCq(&S, j);
        }
    }
    
    printf("遍历队列中元素为:\n");
    CqTraverse(S);
    
    PopCq(&S, &e);
    printf("出队元素为: %d\n",e);
    CqTraverse(S);
    printf("是否为空栈:%d\n",CqEmpty(S));
    getCqHead(S, &e);
    printf("元素:%d \n队列长度:%d\n",e,CqLength(S));
    ClearCqStack(&S);
    printf("是否已经清空队列 %d, 栈长度为:%d\n",CqEmpty(S),CqLength(S));
    
    return 0;
}