从 0 开始机器学习 - 手把手用 Python 实现梯度下降法！

机器学习课程也上了一段时间了，今天就带大家从 0 开始手把手用 Python 实现第一个机器学习算法：单变量梯度下降（Gradient Descent）！

我们从一个小例子开始一步步学习这个经典的算法。

一、如何最快下山？

在学习算法之前先来看一个日常生活的例子：下山。想象一下你出去旅游爬山，爬到山顶后已经傍晚了，很快太阳就会落山，所以你必须想办法尽快下山，然后去吃海底捞。

那最快的下山方法是什么呢？没错就是缩成一个球，然后从最陡的方向直接滚下去，可是我们是人不是球，不能直接滚下去，但是可以借鉴这种方式，改变一下策略。

要想最快下山，其实只需要循环执行以下 3 步骤：

环顾周围找到最陡的一段路
在最陡的一段路上走一段距离
重复以上步骤直到山底

假设你拥有找到目前所在位置最陡路线的能力，那么你只需要重复以上步骤就能以最短时间，最短路程下到山底去吃海底捞啦！

这就是梯度下降法的现实例子，下面来正式学习下梯度下降法的基本思想。

二、梯度下降法基本思想

数学上的梯度下降法步骤跟下山的例子一模一样，只不过换成了数学公式具体表达出来而已，这里用个函数图像来形象解释下：

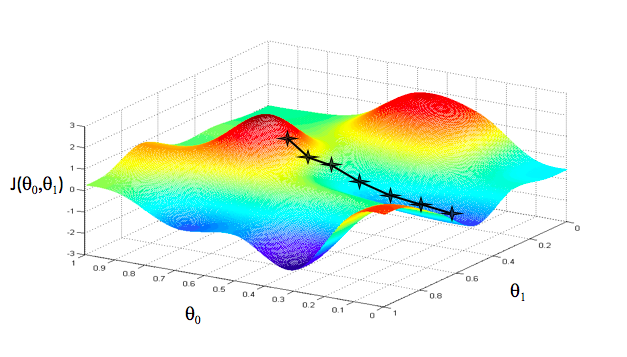
把这个函数图像想象成一座山，此刻你正在山顶，并且要寻找最快的下山路线，那么按照上面讲的下山 3 步骤，你要做的就是找最陡的下山方向，然后走一段路，再找最陡的下山方向，再走一段路，以此类推，最后就得到上面的这条下山路线。

2.1 算法解决什么问题？

我们为了尽快下山，用了梯度下山法；那么对应到数学曲线上，对一个函数应用梯度下降法，就是为了最快地求出函数的全局最小值或者局部最小值；再对应到机器学习问题上，梯度下降法就是为了尽快求出模型代价函数最小值，进而得到模型参数；

所以梯度下降法要解决的问题就是：以最快速度求函数最小值。

2.2 如何用数学公式表达？

先来用公式表达出下山的步骤：

与下山公式一样，一行公式即可写出梯度下降法公式：

{\theta_{j}}={\theta_{j}}-\alpha \frac{\partial }{\partial {\theta_{j}}}J\left(\theta \right)

我们来对照下山的例子，详细解释这个公式：

等式左边的 $\theta_j$ 是下一时刻我在山顶的位置：下一函数值
等式右边的 $\theta_j$ 是当前时刻我在山顶的位置：当前函数值
学习率 $\alpha$ ：算法迭代步长
$-\frac{\partial }{\partial {\theta_j}}J(\theta)$ 是最快的下山方向：当前时刻函数值下降最快的方向
$-\alpha\frac{\partial }{\partial {\theta_j}}J(\theta)$ 是当前时刻的打算迈出的距离：算法当前迭代下降的距离
$J(\theta)$ 可以理解为你要下的那座山：算法执行的函数

这里的 $\alpha$ 在算法中叫做学习率，虽然从名字上不好理解，不过它的作用就是控制算法每次迭代下降的步长，也就是每次下山打算迈开多大步。

你可能疑惑的是下山方向为何加负号，其实在数学上，这个公式 $-\frac{\partial }{\partial {\theta_j}}J(\theta)$ 的意思是求偏导数，也叫做求梯度，函数梯度是函数值增加速度最快的方向，而这里加上一个负号就表示函数值下降最快的方向，也就表示下山速度最快（最陡）的方向。

但是学习率和梯度都不是当前时刻函数值要减少的量，当前函数下降的量等于这两者的乘积 $-\alpha\frac{\partial }{\partial {\theta_j}}J(\theta)$ ，一定不要误以为学习率就是当前函数下降的距离，它只是一种度量方式，可以理解为一个尺度，不是实际的值。

让我们再从实际的梯度下降曲线中直观的看下算法的迭代过程。

三、梯度下降法的直观理解

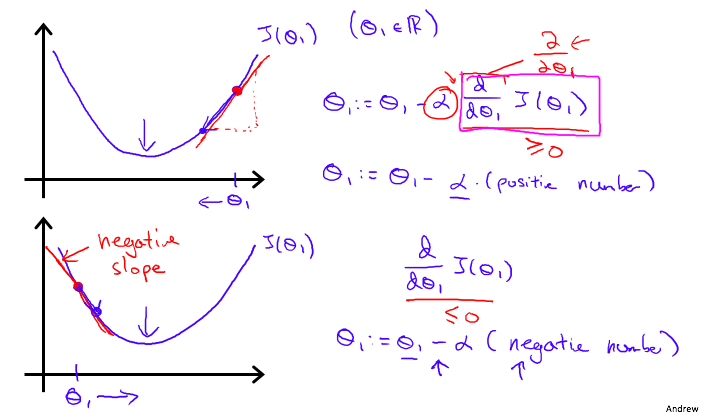
下面这个例子可以很好地解释单变量（ $\theta_1$ ）梯度下降的过程：

算法从曲线的右上角紫色的数据点开始迭代下降，最终下降到底部绿色点找到函数最小值，算法结束，来详细分析一次下降的过程：

计算第一个数据点处的梯度（斜率或偏导数），这里梯度大于 0
计算下一函数值： $\theta_1 = \theta_1 - \alpha * 梯度$
重复以上步骤，直到底部绿色点梯度为 0

这里简单说下学习率 $\alpha$ 对算法的影响：

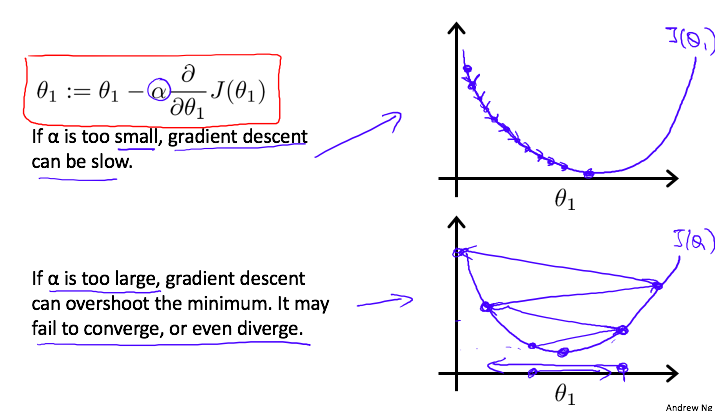
如果 $\alpha$ 太小，每次更新的步长很小，导致要很多步才能才能到达最优点；
如果 $\alpha$ 太大，每次更新步长很大，在快接近最优点时，容易因为步长过大错过最优点，最终导致算法无法收敛，甚至发散；

虽然学习率会影响迭代步长，那是否需要我们每次手动更新学习率呢？

不需要！因为迭代的步长每次都会自动减小！随着数据点越来越靠近最低点，在该点处的斜率越来越小，即梯度值 $\frac{\partial }{\partial {\theta_j}}J(\theta)$ 越来越小，而 $\alpha > 0$ ，所以两者相乘后 $\alpha \frac{\partial }{\partial {\theta_j}}J(\theta)$ 也越来越小，进一步导致 $\theta_j$ 值减小的越来越慢。

当算法最后迭代到最低点时，绿色点处斜率为 0，即梯度为 0，此时梯度下降公式将不再变化：

\theta_j = \theta_j - \alpha * 0 = \theta_j

所以算法认为已经找到最优值，不再迭代下降，算法至此结束。

这个例子是从右向左迭代下降，如果起始数据点是在左边，算法是否能正常运行呢？完全没问题，唯一的不同处是梯度小于 0，公式里面负号变为正号，你可以试着自己分析下。

四、梯度下降法拟合函数直线

理论介绍完了，下面进入实战部分，登龙手把手用 Python 带你实现一个梯度下降法，并用这个的算法来拟合下面的数据点（人口 - 利润）：

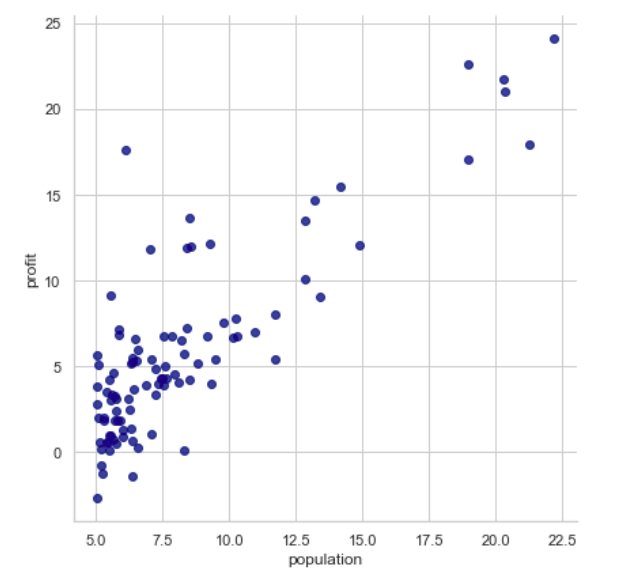
因为篇幅限制，这里只讲解我认为比较关键的代码，其他比较基础的加载数据，导包就不介绍了，文末有完整代码，里面的注释非常详细，建议下载食用，有收获记得回来给我个 Star 哦！

4.1 模型选择

这个数据集比较简单，只有一个人口特征，但是为了方便代码计算我们人为增加一个特征 $x_0 = 1$ ，并且使用线性回归的函数模型：

h_\theta(x) = \theta_0x_0 + \theta_1 x_1

那先来定义这两个参数：

# X.shape[1] = 2，表示参数数量 n = 2
# theta = [theta_0 = 0, theta_1 = 0]
theta = np.zeros(X.shape[1])

我们的最终目的就是找出最优的参数（ $\theta_0$ ， $\theta_1$ ），使得直线拟合的总均方误差达到最小，那如何表示均方误差呢？这就需要代价函数登场了。

4.2 代价函数

代价函数顾名思义就是每组参数所对应的拟合误差量，要想拟合数据集的效果最好，那就要求参数所对应的代价函数取最小值，这里的我选择常用的均方误差来作为代价函数：

J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}

这个代价函数计算的是一组参数（ $\theta_0$ ， $\theta_1$ ）拟合的数据预测值与真实值均方误差，看下这个函数如何用代码写出来，这里要用点线性代数的知识：

# Cost Function
# X: R(m * n) 特征矩阵
# y: R(m * 1) 标签值矩阵
# theta: R(n) 线性回归参数
def cost_function(theta, X, y):
    # m 为样本数
    m = X.shape[0]
    
    # 误差 = theta * x - y
    inner = X @ theta - y
    
    # 将向量的平方计算转换为：列向量的转置 * 列向量
    square_sum = inner.T @ inner
    
    # 缩小成本量大小，这里无特殊含义
    cost = square_sum / (2 * m)
    
    # 返回 theta 参数对应的成本量
    return cost;

我们的梯度下降法就是应用在这个代价函数上，来寻找代价函数的最小值，进而找到取最小值时对应的参数（ $\theta_0$ ， $\theta_1$ ）。

4.3 计算梯度

梯度下降需要用到某点的梯度，即导数，看下求梯度的代码：

# 计算偏导数
def gradient(theta, X, y):
    # 样本数量
    m = X.shape[0]
    
    # 用向量计算复合导数
    inner = X.T @ (X @ theta - y)
    
    # 不要忘记结果要除以 m
    return inner / m

这个其实也不难，就是代价函数对 $\theta_i$ 进行复合求导：

J( \theta_0, \theta_1)' = 2 * \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x_i)-y^{(i)} \right) * h_\theta(x_i)'

h_\theta(x_i)' = (\theta_0x_0 + \theta_1x_1)' = x_i

因为上面的代码是用向量表示的，一列向量里面包含所有参数，所以对包含参数的向量进行乘积，就相当于公式里面的求和符号了，而且使用向量计算，顺序会有点不一样，这里就不详细展开讲了，暂时能理解就可以。

4.4 执行批量梯度下降算法

准备就绪，下面就到了最重要的部分，批量梯度下降法的逻辑代码，其实也很简单，就是执行一个循环 =_=：

# 批量梯度下降法
# epoch: 下降迭代次数 500
# alpha: 初始学习率 0.01
def batch_gradient_decent(theta, X, y, epoch, alpha = 0.01):
    # 计算初始成本：theta 都为 0
    cost_data = [cost_function(theta, X, y)]
    
    # 创建新的 theta 变量，不与原来的混淆
    _theta = theta.copy()
    
    # 迭代下降 500 次
    for _ in range(epoch):
        # 核心公式：theta = theta - 学习率 * 梯度
        _theta = _theta - alpha * gradient(_theta, X, y)
        
        # 保存每次计算的代价数据用于后续分析
        cost_data.append(cost_function(_theta, X, y))
    
    # 返回最终的模型参数和代价数据
    return _theta, cost_data

传入的参数我们之前都介绍过了，再复习下：

theta：待预测的直线参数 $\theta_j$
X：样本横坐标值
y：样本纵坐标值
epoch：迭代下降次数
alpha：学习率

最终返回的结果是迭代 500 次后对原始数据拟合误差最小的参数 $\theta_0, \theta_1$ 以及每次计算的代价数据 $cost$ 。

补充下：这里批量的意思是每次迭代都计算全部样本的均方误差，不是一次计算一个样本，只是我们常常省略批量这两个字，直接叫梯度下降法。

4.5 测试拟合结果

我们来调用上面的批量梯度下降法，看下预测的参数：

epoch = 500
final_theta, cost_data = batch_gradient_decent(theta, X, y, epoch)

final_theta

输出 $\theta_0 = -2.2828, \theta_1 = 1.0309$ ：

array([-2.28286727,  1.03099898])

来可视化代价数据看下是否连续下降：

cost_data

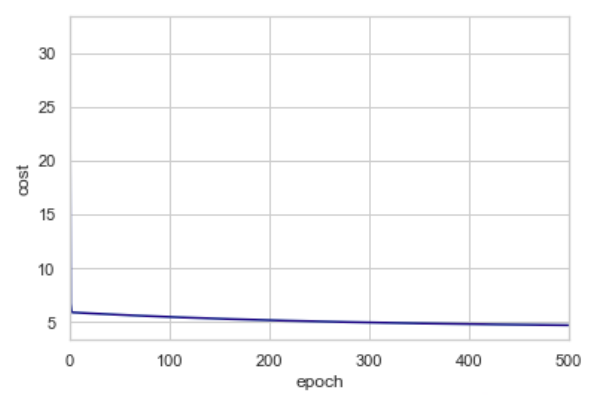
代价函数随着迭代次数变多逐渐减小，直到 4.713809 基本不变，至此我们已经找到了我们认为的最优的拟合数据的直线模型参数，因为代价函数取得了最小值。

那来看下拟合的效果，看起来还不错：

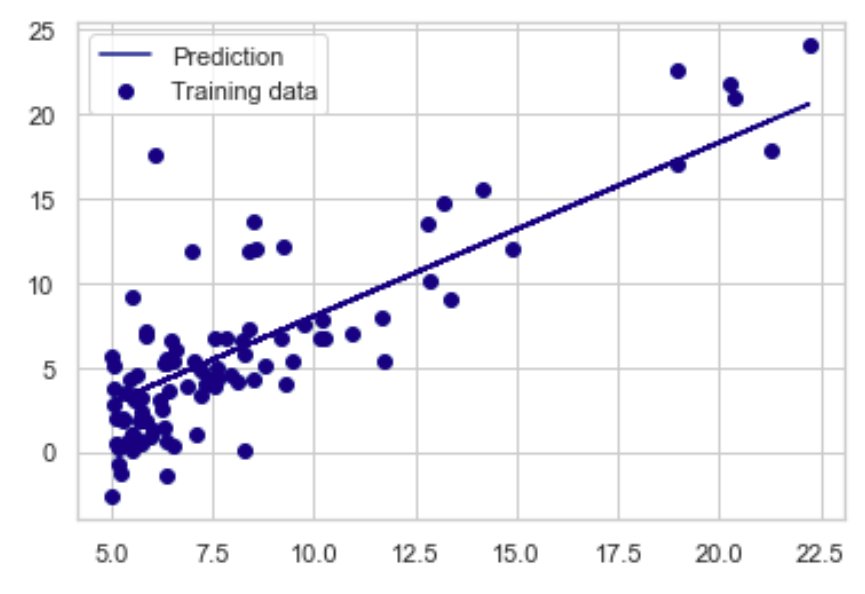
五、总结

以上就是我对单变量梯度下降法的基本理解，还有很多不足，希望大家多多指正，文中部分代码用到微积分和线性代数的知识，建议回头复习下，可以更好的理解算法 ^_^！

另外，关于多变量的梯度下降法我也写了点自己的总结：从 0 开始机器学习 - 一文入门多维特征梯度下降法！，原理几乎相同，强烈推荐实践一下。

文中项目超详细注释完整代码：AI-Notes，学会了记得回来给我个 Star 哈。

本文原创首发于同名微信公号「登龙」，微信搜索关注回复「1024」你懂的！