排序算法(冒泡、插入、选择)

2020年04月07日 19:30

冒泡排序

冒泡排序只会操作相邻的两个数据，每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足，就让他俩互换。一次冒泡会至少让一个元素移动到它应该在的位置，重复n次，就完成了n个数据的排序工作

代码：

func bubbleSort(nums []int) {
    if len(nums) <= 1 {
        return 
    }
    for i := 0 ; i < len(nums)-1; i ++ { //控制趟数，
        //当某次冒泡操作已经没有数据交换时，说明已经达到完全有序。不需要再进行后续冒泡操作
        flag := false // 提前退出冒泡循环的标志位
        for j :=0; j < len(nums)-1-i; j ++ { //控制要交换的次数
            if nums[j] > nums[j+1] {
                nums[j], nums[j+1] = nums[j+1], nums[j]
                flag = true
            }
        }
        if !flag {
            break
        }
    }
}

复制代码

第一，冒泡排序是原地排序算法吗？

冒泡排序的过程只涉及相邻元素之前的交换，只需要常量级别的内存临时空间，所以它的空间复杂度为 O(1)，是一个原地排序算法。

第二，冒泡排序是稳定的排序算法吗？

在冒泡排序中，只有交换才可以改变两个元素的前后顺序，为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，我们不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序算法是稳定的。

第三，冒泡排序的时间复杂度是多少？

最好情况下，要排序的数据已经是有序的了，我们只需要进行一次冒泡操作，就可以结束了，所以最好情况时间复杂度是 O(n)。
而最坏的情况是，要排序的数据刚好是倒序排列的，我们需要进行 n 次冒泡操作，所以最坏情况时间复杂度为 O(n2)。
平均情况下的时间复杂度就是 O(n2)。

插入排序

将数组中的数据分为两个区间，已排序区间和未排序区间。初识已排序区间只有一个元素，就是数组的第一个元素。插入排序的核心思想就是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间仍然有序。重复这个过程，直到未排序区间中元素为空，算法介绍书

代码：

func insertionSort(nums []int) {
    if len(nums) <= 1 {
        return 
    }
    for i := 1; i < len(nums); i ++ { //遍历未排序空间，默认第一个元素，即下标未0的元素为已排序元素。
        value := nums[i] //value标识未排序区间的第一个元素
        j := i-1  //j 标识已排序区间的最后一个元素
        for ; j >= 0; j -- {  //从已排序区间最后一个元素往前找
            if nums[j] > value {   //如果已排序区间元素大于未排序区间的元素，则需要插入
                nums[j+1] = nums[j] //将已排序区间元素后移
            } else {
                break   //否则就break，不用再继续比较，因为是从已排序区间最大的开始遍历的。
            }
        } 
        nums[j+1] = value //最后将元素插入，此时j+1 表示为合适的位置（为什么j+1，因为退出时j--）
        //1. 如果break了，能确保i+1 为 i的位置，赋值为原下标的值
        //2. 如果未进入break循环，j--后，j+1能保证为原来的位置
    }
}
复制代码

第一，插入排序是原地排序算法吗？

插入排序算法的运行并不需要额外的空间，所以空间复杂度为O(1),是就地排序的。

第二，插入排序是稳定的排序算法吗？

在插入排序中，对于值相等的元素，我们可以选择将后面出现的元素，插入到前面出现的元素后面，这样就可有保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

第三，插入排序的时间复杂度是多少？

如果要排序的数据已经是有序的，我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置，每次只需要比较一个数据就能确定插入的位置。所以这种情况下，最好是时间复杂度为 O(n)。注意，这里是从尾到头遍历已经有序的数据。
如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，所以最坏情况时间复杂度为 O(n2)。
还记得我们在数组中插入一个数据的平均时间复杂度是多少吗？没错，是O(n)。所以，对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行 n 次插入操作，所以平均时间复杂度为 O(n2)。

选择排序

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

代码：

func SelectionSort(nums []int) {
    if len(nums) <= 1 {
        return 
    }
    for i := 0; i < len(nums); i ++ {  //从第一个元素遍历
        minIndex := i   // 默认取第一个元素为最小值
        for j := i+1; j < len(nums); j ++ { //遍历第一个元素后的所有元素
            if nums[j] < nums[minIndex] {   
                minIndex = j
            }
        }
        nums[i], nums[minIndex] = nums[minIndex], nums[i] //交换位置
    }
}
复制代码

三种算法比较

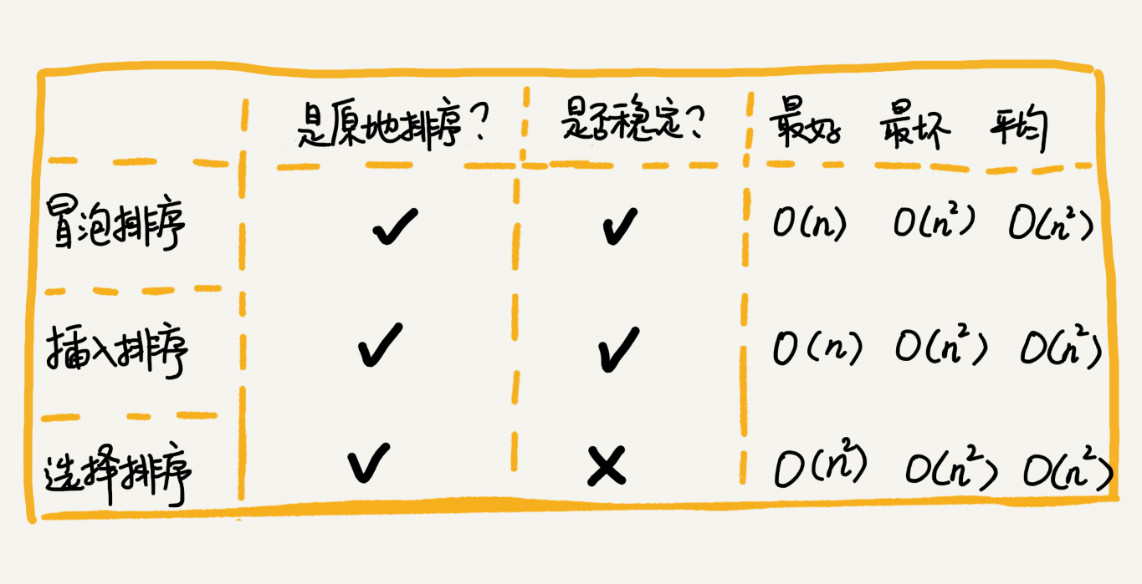
冒泡排序和插入排序的时间复杂度都是 O(n2)，都是原地排序算法，为什么插入排序要比冒泡排序更受欢迎呢？

冒泡排序不管怎么优化，元素交换的次数是一个固定值，是原始数据的逆序度。插入排序是同样的，不管怎么优化，元素移动的次数也等于原始数据的逆序度。
但是从代码实现上看，冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要3个赋值操作，而插入排序只需要一个。
我写了一个性能对比测试程序，随机生成 10000 个数组，每个数组中包含 200 个数据，然后在我的机器上分别用冒泡和插入排序算法来排序，冒泡排序算法大约 700ms 才能执行完成，而插入排序只需要 100ms 左右就能搞定！