BatchNorm在NLP任务中的问题与改进众所周知，无论在CV还是NLP中，深度模型都离不开归一化技术（Normali

众所周知，无论在CV还是NLP中，深度模型都离不开归一化技术（Normalization）。在CV中，深度网络中一般会嵌入批归一化（BatchNorm，BN）单元，比如ResNet；而NLP中，则往往向深度网络中插入层归一化（LayerNorm，LN）单元，比如Transformer。

为什么在归一化问题上会有分歧呢？一个最直接的理由就是，BN用在NLP任务里实在太差了（相比LN），此外，BN还难以直接用在RNN中[1]，而RNN是前一个NLP时代的最流行模型。

虽然有大量的实验观测，表明NLP任务里普遍BN比LN差太多，但是迄今为止，依然没有一个非常严谨的理论来证明LN相比BN在NLP任务里的优越性。甚至，连BN自身为什么work的问题都一直存在争议。

早期对BN有效性的解释是其有助于缓解神经网络“内部协方差漂移”（Internal Covariance Shift，ICS）问题。即，后面的层的学习是基于前面层的分布来的，只有前面一层的分布是确定的，后面的层才容易学习到有效的模式，然而，由于前面的层的分布会随着batch的变化而有所变动，导致了后面的层看来“前面一直在动，我无法安心学习呀”。

而BatchNorm这类归一化技术，目的就是让每一层的分布稳定下来，让后面的层可以在前面层的基础上安心学习知识。顾名思义，BatchNorm就是通过对batch size这个维度归一化来让分布稳定下来。LayerNorm则是通过对Hidden size这个维度归一化来让某层的分布稳定。

然而，后来也有一些研究diss了这个解释，说这个解释是错误或不充分的（incorrect/incomplete）[2]，近期也有一些研究[3][4]表明BN之所以有助于训练深度神经网络，是因为它可以让loss曲面变得更加平滑。Anyway，这依然是一个未完全解开的老谜。

除了BN之外，LN也有同样的“为什么work”的终极问题。研究[5]表明，LN在反向时有助于梯度的归一化。也有研究[6][7]表示LN的主要作用是在训练初期缓解梯度消失和爆炸的问题，提升稳定性。

所以说，BN和LN本身的作用机理都没有完全搞清楚，自然也很难去证明为什么BN在NLP数据上就不work，LN就更work。

不过，近期小夕无意间刷到了一篇UC Berkeley的《Rethinking Batch Normalization in Transformers》[8]，发现了一个比较有趣的实验结论，并基于这个观测，作者提出了一种针对NLP data（确切说是Transformer）改进的新的归一化方法，叫幂归一化（PowerNorm）。

强上BN后的Transformer

作者这里做了一个实验，为BN在NLP data（Transformer）上不work提供了一个更加微观的观测证据。

首先，作者将Transformer中的LN都替换成了BN，然后在CV和NLP两个任务上观测BN中的两个统计量（即均值 $\mu$ 和方差 $\sigma^2$ ）及其他们的梯度 $g_\mu$ 和 $g_{\sigma^2}$ 在训练过程中的稳定程度。

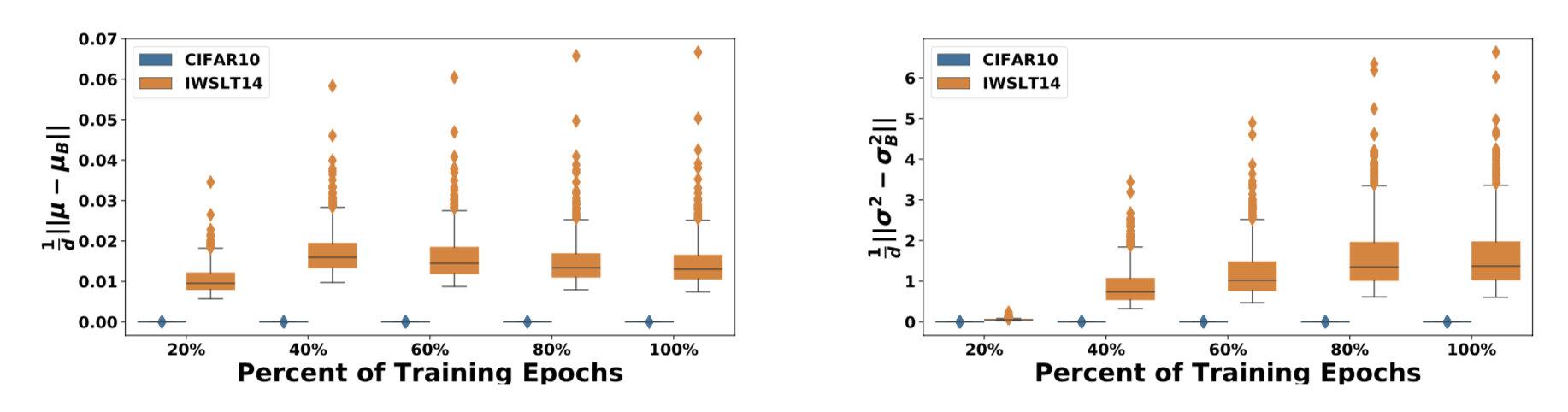
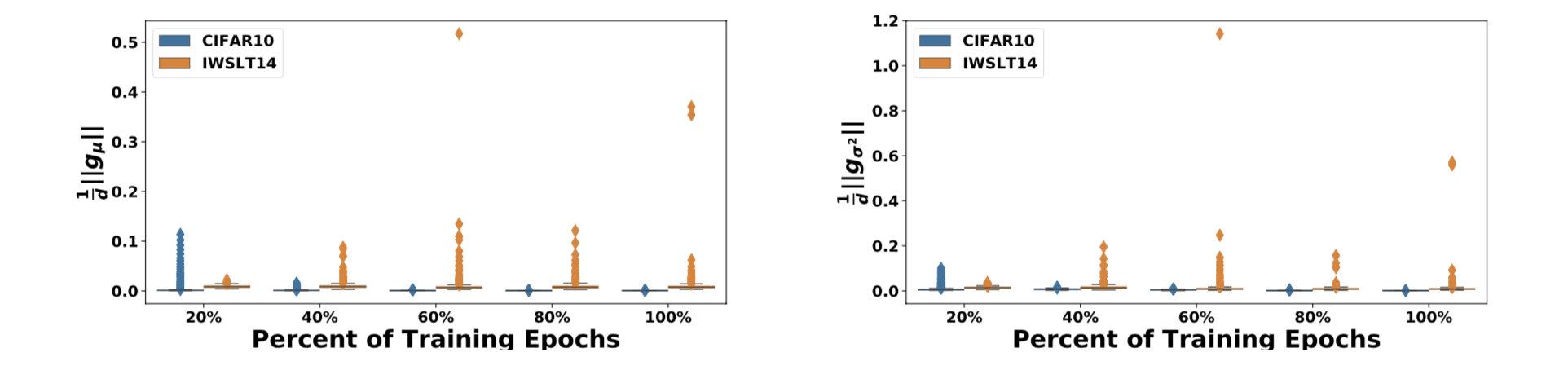
上图中，蓝色是ResNet20在Cifar-10做图像分类的结果，橙色是Transformer+BN在IWSLT14做翻译的结果。X轴是训练时间，Y轴是基于batch的统计值和它对应的移动平均值的欧式距离。

可以看到，ResNet20在Cifar-10任务上统计量的震荡很小，而使用BN的Transformer不仅震荡剧烈，还有很极端的异常值，这会导致 $\mu$ 和 $\sigma$ 的统计不准确，造成train/test不一致，预测效果下降。

基于这个有趣的观测结果，作者这里针对性的提出了两点改进，并将改进后的BN称之为幂归一化（PowerNorm，PN）。

PowerNorm

1. PN-V

BN强制将数据转换成均值为0方差为1的正态分布，但在数据本身均值方差剧烈震荡的情况下，强制移动均值会起到不好的效果。因此作者提出了新的scale方式，只强制数据有unit quadratic mean：

$\psi_B^2 = \frac{1}{B}\sum{x_i^2} \\$ $\hat{X} = \frac{X}{\psi_B} \\$ $Y = \gamma\cdot\hat{X} + \beta \\$

这样针对batch的前向只需一个统计量，反向也简化成 $g_{\psi^2}$ 一个梯度：

$\frac{\partial{\mathcal{L}}}{\partial{x_i}} = \frac{1}{\psi_B\gamma}\frac{\partial{\mathcal{L}}}{\partial{y_i}}-\frac{1}{\psi_B\gamma B}\sum_{j\in B}(\frac{\partial{\mathcal{L}}}{\partial{y_j}}\hat{x_i}\hat{x_j}) \\$

对比新的 $\psi$ （橙色）和之前的 $\sigma$ （蓝色），发现震荡明显减小：

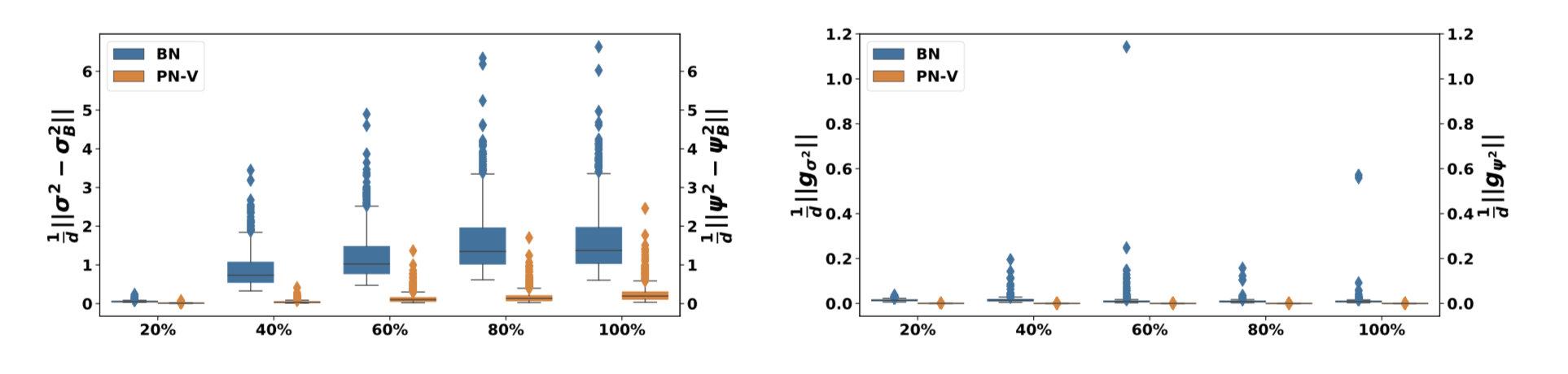
2. Running Statistics in Training

从PN-V的改进可以看到，虽然震荡减少了很多，但还是有很多异常值。因此作者改用移动平均的方式计算 $\psi$ ：

$\hat{X_t} = \frac{X_t}{\psi_{t-1}} \\$ $Y_t = \gamma\cdot\hat{X_t} + \beta \\$ $\psi^2_t = \alpha\psi^2_{t-1} + (1-\alpha)\psi_B^2 \\$

但使用移动平均的话，在求梯度时无法对之前所有 $\psi$ 求导，因此作者用当前batch的统计量去近似，感兴趣的同学可以看下论文中的推导。

与LN的比较

虽然如前所述，难以说清楚在NLP data上LN比BN优越在哪里，但是是容易说清楚PN对BN的优越性的（毕竟PN的诞生就是基于BN在NLP data上的实验观测）。

那么问题来了：PN和LN哪个更有效？自然也没法直接在理论层面上进行比较，所以作者跑了一把实验，分别尝试了机器翻译和语言模型任务：

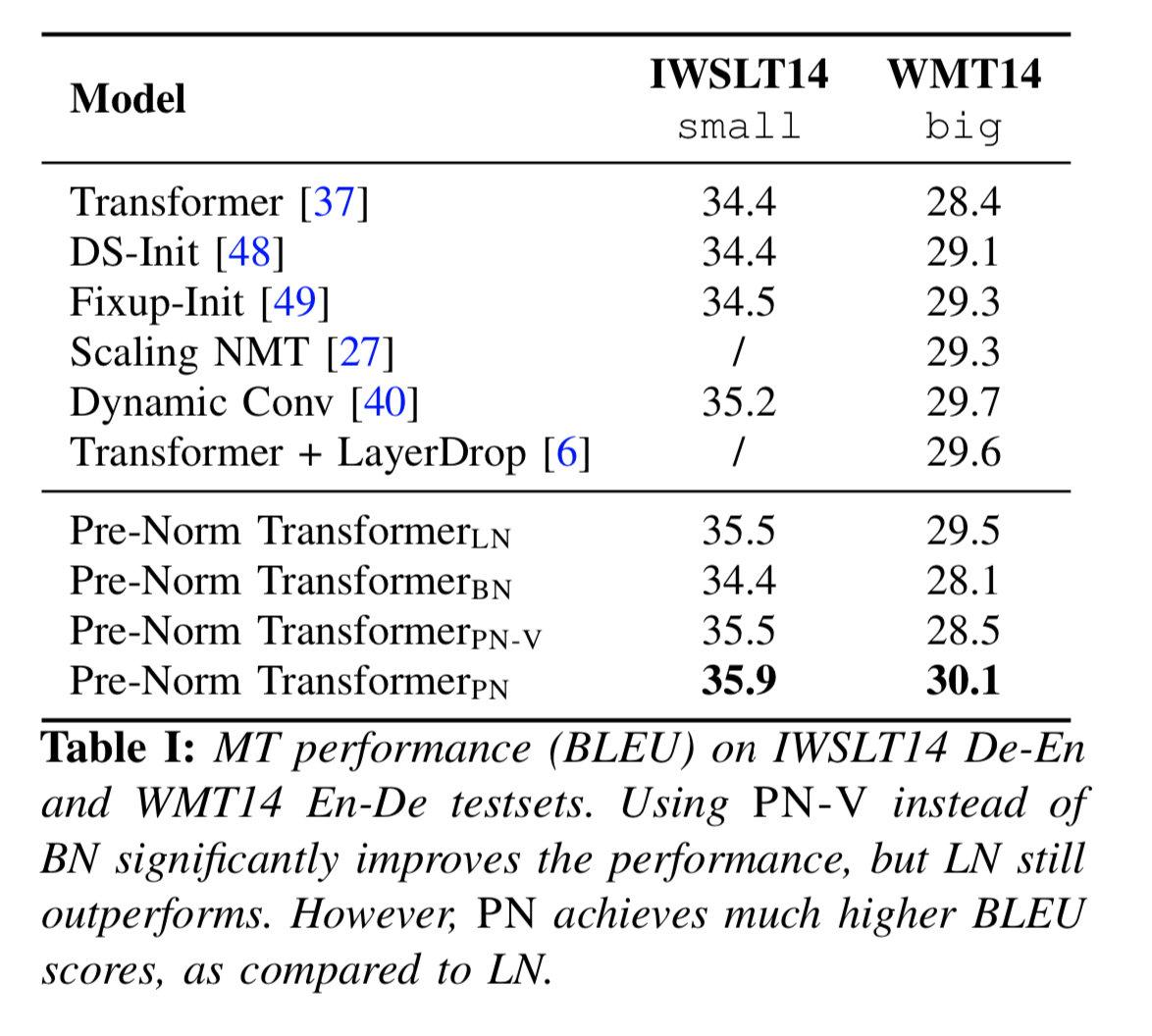
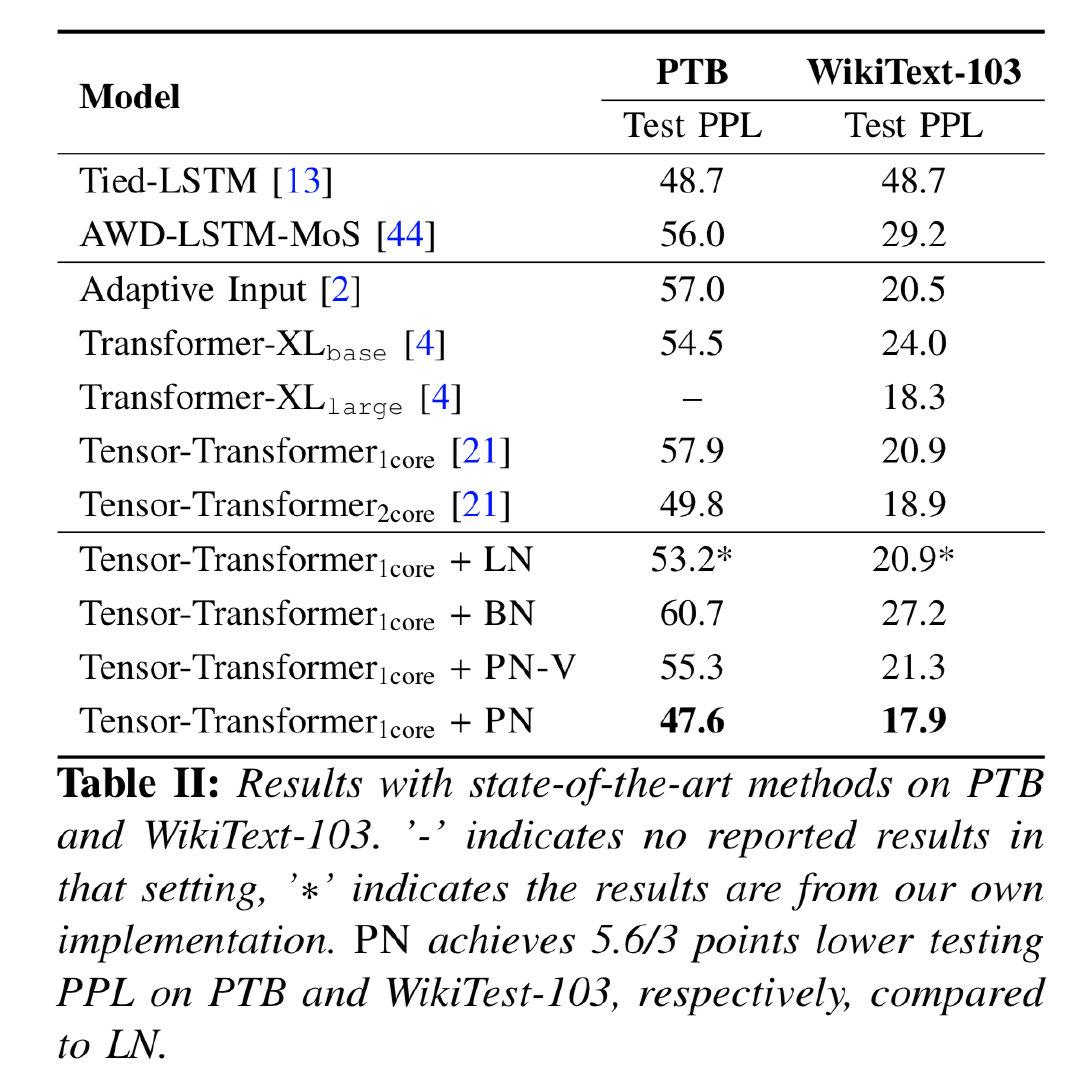
对于上述结果，小夕也去paperwithcode网站查了一下，目前IWSLT14的SOTA是36.3，论文中的35.9可以排在第二的位置；WMT14 En-De的SOTA是35，论文中的30.1可以排在第五的位置；WikiText-103的SOTA是10.8，论文的结果排在第八名第位置。由于作者没有做其他优化，看起来总体结果还是不错的～当然，PN在其他NLP data和任务上是否有效，还有待进一步验证。

由于BN和PN的统计量受batchsize的影响，作者在消融实验中也探究了不同batchsize的效果：

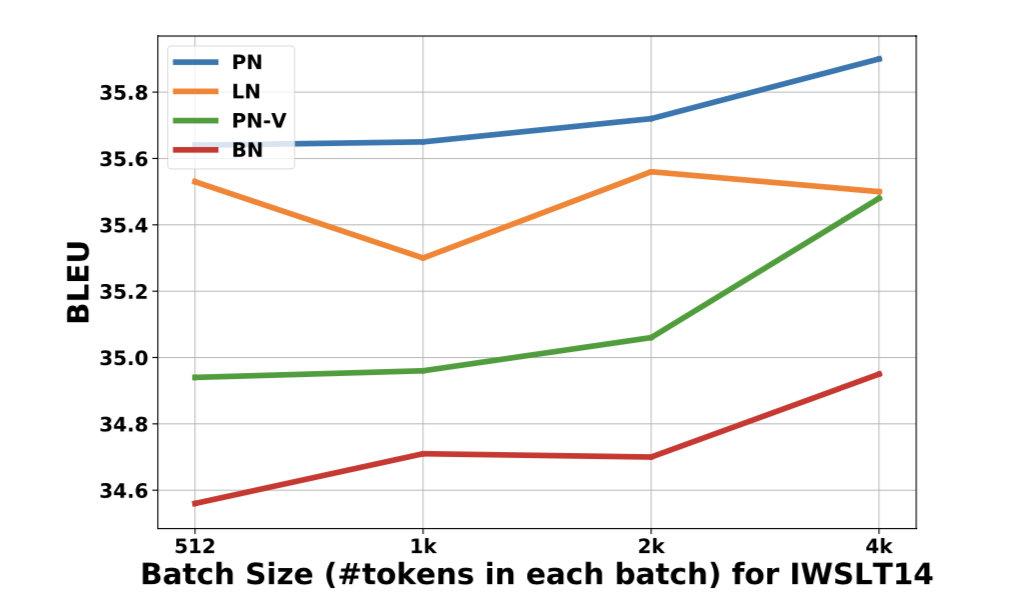
可以看到PN在整体上还是优于LN的。

总结

由于深度学习的不可解释性，归一化方法在网络中真正的作用和优劣一直是个谜。本文针对BN提供了一个新的研究角度，通过对统计量及梯度的稳定性观测，找到了BN为什么在NLP问题上不work的其中一个原因，即数据分布的震荡和异常值导致train/test不一致。基于该观测证据，作者对BN进行了对应的改进，提出了更适合NLP data的幂归一化PowerNorm，得到了优于原生BN的效果，且在部分任务上超过了LN的表现。

另外，大多数同学可能更关心用PN改进BERT的表现，但目前来看还是比较难验证的。如果要验证BERT，那肯定不能直接在精调阶段替换LN，必须要经过预训练才能验证。如果要预训练，那首先需要复现BERT，和谷歌官方结果对齐，这可能就需要几个月的时间=。= 等真正搞了预训练之后，就会发现这些结构上的细节并不重要，语料及预处理、预训练任务都对效果有更大的影响。

所以目前结构创新都不会用BERT去验证，机器翻译和LM任务确实是常规benchmark。是否真正有用，可能需要慢慢被大家用起来才知道。

backup

BatchNorm自2015年提出后一直被广泛应用于深度学习模型中，也衍生了一系列Normalisation的方法，其实本质上都在解决两个问题：

Internal covariance shift：对于神经网络中的某一层来说，理论上是希望输入数据的分布保持一致，保证泛化能力。然而真实情况中每个batch中的数据都是不同的，很难保持一致的分布。
梯度消失：由于数据维度的增加，很容易在点积计算时得到非常大的数值，落在非线性函数的饱和区，导致梯度消失。

对于这些问题，normalisation的解决方案是将网络中的输入数据或者参数进行变换。设某层网络为 $f_W(X)$ ，其中 $W$ 为网络参数， $X$ 为当层输入。根据变换的对象不同，normalisation主要分为以下两种方式：

Weight normalisation[9]

对参数W进行归一化，将W分解为模长 $g$ 和方向 $v$ 两部分：

$W = g \frac{v}{||v||} \\$

这样，最基本的线性投影就可以变成：

$f_W(X) = WX = v \cdot g\cdot\frac{X}{||v||} \\$

相当于用 $||v||$ 对X进行scale，调整分布且缓解梯度消失的问题。

Activation normalisation

对输入数据X进行归一化，典型方法如Batchnorm和Layernorm。以BN为例，它先对数据进行shift和scale，变换到标准正态分布：

$\mu = \frac{1}{N}\sum{x} \\$ $\sigma^2 = \frac{1}{N}\sum{(x-\mu)^2} \\$ $\hat{X} = \frac{X-\mu}{\sigma} \\$

但如果每层都是相同的分布，且数值都落在激活函数的线性区域的话会降低模型的表达能力，所以会把归一化的分布再次进行变换：

$Y = \gamma\cdot\hat{X} + \beta \\$

这样就对网络的输入数据分布进行了调整。

本次的新研究提出的PowerNorm是对BatchNorm的改进，属于activation normalisation的一种。

BatchNorm的问题

虽然BatchNorm在CV中应用广泛，但NLP最常用的还是LayerNorm。LN对数据的归一化方式与BN一样，唯一的不同是 $\mu$ 和 $\sigma$ 的统计维度。BN是在batch维度上分别统计每个feature的均值方差，而LN是在feature维度统计当前层的均值和方差。

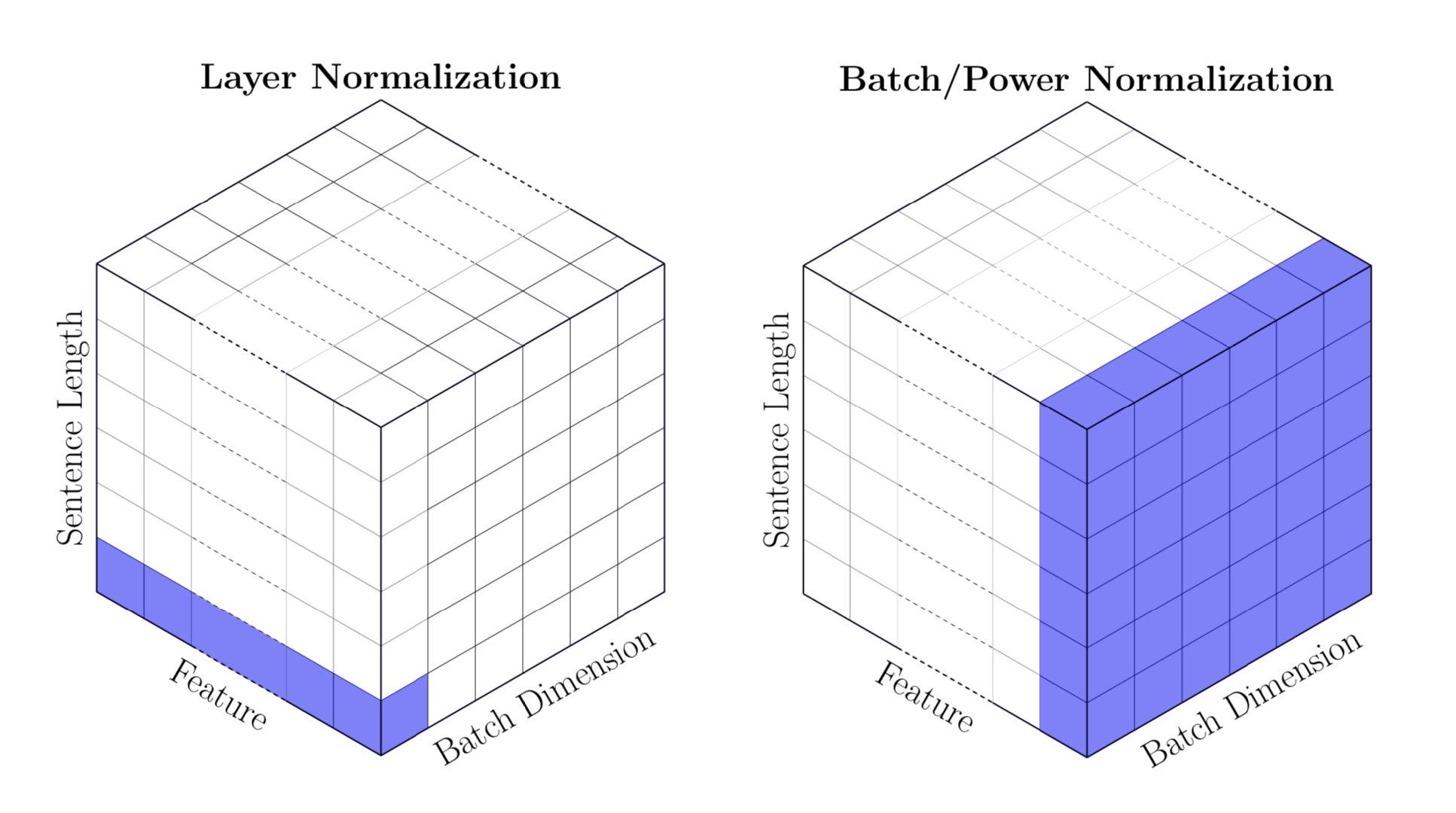
对于NLP任务，BN的应用仍然较少的原因主要有两点，一是BN的效果会受batchsize这个超参影响；二是NLP任务的输入的维度通常是[batch_size, seq_len, hidden_dim]，因此BN得到的均值和方差维度为[1, 1, hidden_dim]。而NLP的句子通常是不定长的，如果长句和短句一起统计，短句后面的[PAD] token会影响统计值。因此BN在NLP任务中表现通常较差，炼丹师们更倾向采用LN。

本文的作者通过观察统计量，发现了BN在训练时的另一个问题，即前后向计算时统计量震荡过大。BN在前向时需要计算 $\mu$ 和 $\sigma$ 两个统计量，在反向计算梯度时也有两个，可以从loss对x的偏导推出：

$\begin{align} \frac{\partial{\mathcal{L}}}{\partial{x_i}} &= \frac{\partial{\mathcal{L}}}{\partial{\hat{x_i}}}\frac{\partial{\hat{x_i}}}{\partial{x_i}} + \sum_{j\in B}(\frac{\partial{\mathcal{L}}}{\partial{\hat{x_j}}}\frac{\partial{\hat{x_j}}}{\partial{\mu}}\frac{\partial{\mu}}{\partial{x_i}}+\frac{\partial{\mathcal{L}}}{\partial{\hat{x_j}}}\frac{\partial{\hat{x_j}}}{\partial{\sigma}}\frac{\partial{\sigma}}{\partial{x_i}}) \\ &=\frac{1}{\sigma}\frac{\partial{\mathcal{L}}}{\partial{\hat{x_i}}} + \sum_{j\in B}\frac{\partial{\mathcal{L}}}{\partial{\hat{x_j}}} (\frac{\partial{\hat{x_j}}}{\partial{\mu}}\frac{1}{B}+\frac{\partial{\hat{x_j}}}{\partial{\sigma^2}}\frac{2}{B}(x_i-\mu)) \\ &=\frac{1}{\sigma}\frac{\partial{\mathcal{L}}}{\partial{\hat{x_i}}} - \frac{1}{\sigma B} \sum_{j\in B}\frac{\partial{\mathcal{L}}}{\partial{\hat{x_i}}}(1+\frac{x_i-\mu}{\sigma}\frac{x_j-\mu}{\sigma}) \\ &=\frac{1}{\sigma}\frac{\partial{\mathcal{L}}}{\partial{\hat{x_i}}} - \frac{1}{\sigma B} \sum_{j\in B}\frac{\partial{\mathcal{L}}}{\partial{\hat{x_i}}}(1+\hat{x_i}\hat{x_j}) \end{align} \\$

其中B代表batch。

若 $\frac{\partial{\mathcal{L}}}{\partial{Y}}$ 已知，有 $\gamma\cdot\frac{\partial{\mathcal{L}}}{\partial{\hat{X}}}=\frac{\partial{\mathcal{L}}}{\partial{Y}}$ ，则上式可转换为

$\frac{\partial{\mathcal{L}}}{\partial{x_i}} = \frac{1}{\sigma\gamma}\frac{\partial{\mathcal{L}}}{\partial{y_i}}-\frac{1}{\sigma\gamma B}\sum_{j\in B}(\frac{\partial{\mathcal{L}}}{\partial{y_j}}+\frac{\partial{\mathcal{L}}}{\partial{y_j}}\hat{x_i}\hat{x_j}) \\$

我们把来自 $\mu$ 的梯度 $\frac{\partial{\mathcal{L}}}{\partial{y_j}}$ 命名为 $g_\mu$ ，来自 $\sigma$ 的梯度 $\frac{\partial{\mathcal{L}}}{\partial{y_j}}\hat{x_i}\hat{x_j}$ 命名为 $g_{\sigma^2}$ 。这样BN在前向时主要有针对batch的 $\mu_B$ 和 $\sigma_B$ 两个统计量，在反向时有 $g_\mu$ 和 $g_{\sigma^2}$ 两个关于batch统计量的梯度。

作者分别统计了CV和NLP两个任务下这些统计量的表现（ResNet20在Cifar-10做图像分类，Transformer+BN在IWSLT14做翻译），发现Transformer+BN时（橙色）这四个统计量震荡很大：

其中 $\mu$ 和 $\sigma$ 是不针对batch的运行时统计量，通过各个 $\mu_B$ 和 $\sigma_B$ 的移动平均计算得到，作为inference时的均值和方差。

可以看到，ResNet20在Cifar-10任务上统计量的震荡很小，而Transformer+BN中不仅震荡剧烈，还有很极端的异常值，这会导致 $\mu$ 和 $\sigma$ 的统计不准确，造成train/test不一致，预测效果下降。

PowerNorm

针对上述BN在Transformer中的缺点，作者提出了PowerNorm，对BN进行了两点改进.

1. PN-V

$\psi_B^2 = \frac{1}{B}\sum{x_i^2} \\$ $\hat{X} = \frac{X}{\psi_B} \\$ $Y = \gamma\cdot\hat{X} + \beta \\$

这样针对batch的前向只需一个统计量，反向也简化成 $g_{\psi^2}$ 一个梯度：

对比新的 $\psi$ （橙色）和之前的 $\sigma$ （蓝色），发现震荡明显减小：

2. Running Statistics in Training

从PN-V的改进可以看到，虽然震荡减少了很多，但还是有很多异常值。因此作者改用移动平均的方式计算 $\psi$ ：

$\hat{X_t} = \frac{X_t}{\psi_{t-1}} \\$ $Y_t = \gamma\cdot\hat{X_t} + \beta \\$ $\psi^2_t = \alpha\psi^2_{t-1} + (1-\alpha)\psi_B^2 \\$

但使用移动平均的话，在求梯度时无法对之前所有 $\psi$ 求导，因此作者用当前batch的统计量去近似，感兴趣的同学可以看下论文中的推导。

改成移动平均后，不会有train/test不一致的问题，效果有了明显提升。作者分别尝试了机器翻译和语言模型任务：

由于BN和PN的统计量受batchsize的影响，作者在消融实验中也探究了不同batchsize的效果：

可以看到PN在整体上还是优于LN的。

总结

这篇文章针对BN进行了改进，提出了PowerNorm新方法，只对数据进行scale而放弃了shift。得到了优于LayerNorm的效果。

另外，看到这里后，相信会有很多小伙伴会关心BERT+PN的效果。燃鹅众所周知，要复现BERT的预训练过程是非常不可描述的，所以作者这里没有给出相应实验，也是合乎情理的。

所以目前结构创新都很少用BERT去验证，机器翻译和LM任务确实是常规benchmark。是否真正有用，可能需要慢慢被大家用起来才知道。

参考资料

[1] RNN为什么不适合做BN？: https://www.zhihu.com/question/308310065/answer/569167072,

[2] Ali Rahimi. Nuerips 2017 test-of-time award presentation, December 2017: https://www.zachpfeffer.com/single-post/2018/12/04/Transcript-of-Ali-Rahimi-NIPS-2017-Test-of-Time-Award-Presentation-Speech,

[3] How does batch normalization help optimization?: https://papers.nips.cc/paper/7515-how-does-batch-normalization-help-optimization.pdf,

[4] PyHessian: Neural networks through the lens of the Hessian.: https://arxiv.org/pdf/1912.07145.pdf,

[5] Understanding and Improving Layer Normalization: https://arxiv.org/abs/1911.07013,

[6] Improving Deep Transformer with Depth-Scaled Initialization and Merged Attention: https://arxiv.org/abs/1908.11365,

[7] Fixup Initialization: Residual Learning Without Normalization: https://arxiv.org/abs/1901.09321,

[8] Rethinking Batch Normalization in Transformers: https://arxiv.org/abs/2003.07845,

[9] 详解深度学习中的Normalization，BN/LN/WN: https://zhuanlan.zhihu.com/p/33173246,