由于逻辑回归是一个伯努利分布,所以逻辑回归本质是交叉熵(作为损失函数)
逻辑回归和交叉熵对于MSE顾虑都一样,cost function = (y-a)^2,对于神经网络而言,会降低w,b的更新速度,而对于逻辑回归来说,MSE会导致代价函数非凸,存在很多局部最优解。
先了解信息熵和相对熵

信息熵的本质的另一种解释:最短平均编码长度
交叉熵:本质含义:编码方案不一定完美时,平均编码长度的是多少】
相对熵本质含义:由于编码方案不一定完美,导致的平均编码长度的增大值】
相对熵---KL散度
相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异。
公式如下:
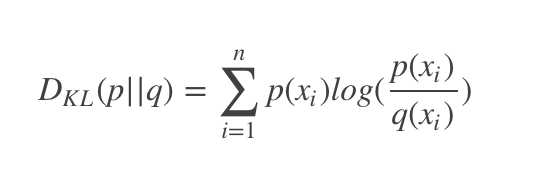
其中P表示真实分布,而Q表示估计分布。假如P=[1,0,0], Q = [0.7,0.2,0,1],那么表示需要一些信息增量才能完全描述这个P分布
交叉熵
先摆上信息熵的公式:(信息熵在另一片文章)
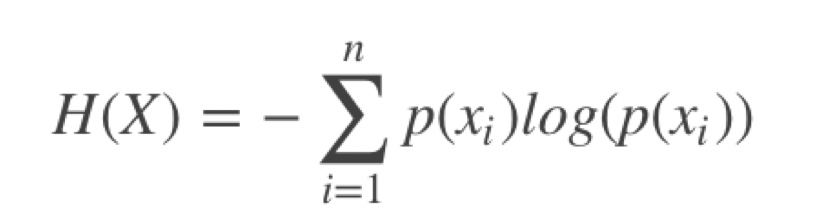
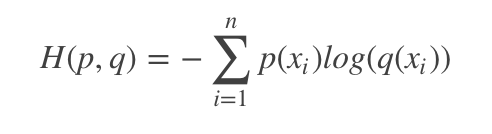
相对熵=信息熵-交叉熵
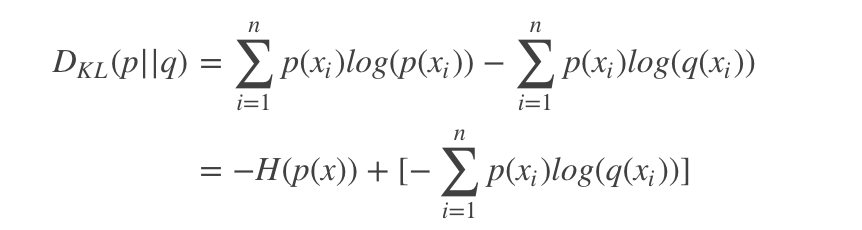
那么从上面可以看出,信息熵是不变的,变得只有交叉熵,而相对熵刚好可以帮我们评估label和prediction之间的差异,所以在优化过程中只用交叉熵即可。
推导前
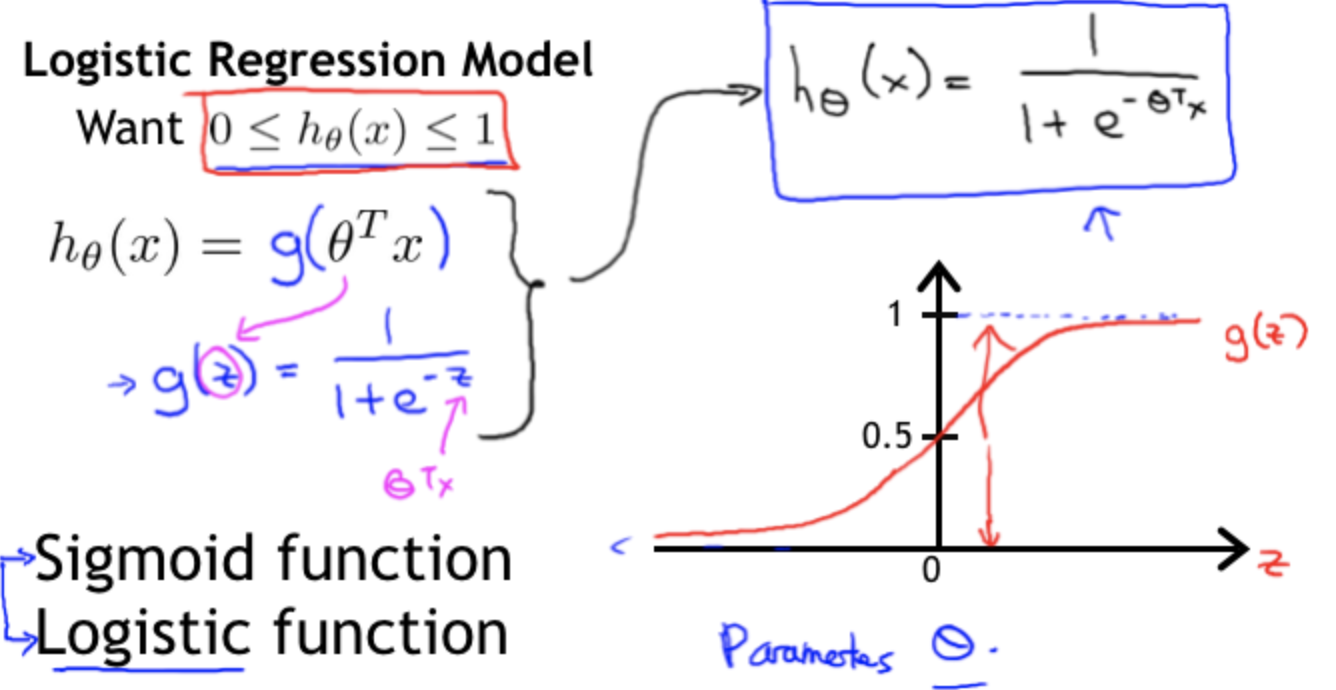
模型中有目标函数即h(x),激活函数g(x), h(x) = g(θX)
代入不同的目标函数和激活函数得到不同的模型,如g()为sigmoid,h()为线性,就是逻辑回归了。
推导1
对于二分类问题,交叉熵满足伯努利分布。
二分类问题用到sigmoid(softmax),即有推导:


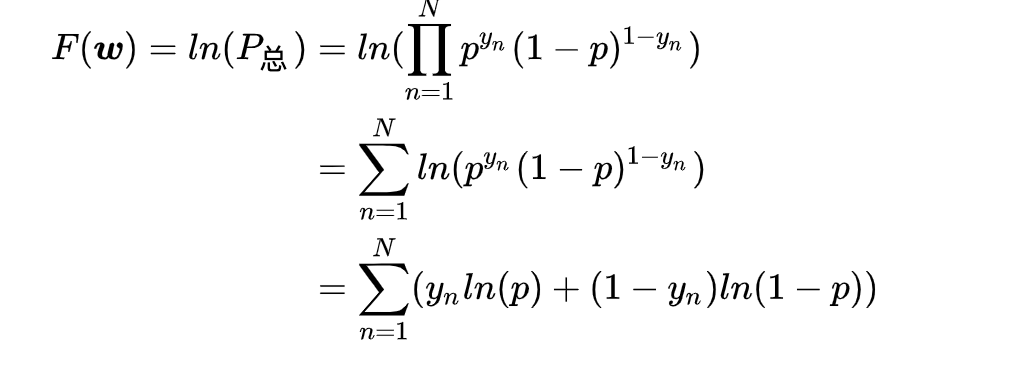
一路推下来会有最下面那个。
然后,我们搞的是cost function越小越好,但在式子中我们希望的是F(w)越大越好,那么直接加负号(下面式子log跟ln是一样的没影响):
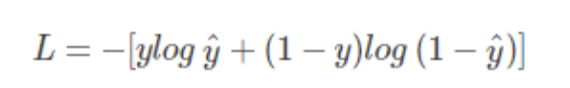
另一种:


推导2
其中a=σ(z)就是我们的目标函数,z=wx+b, σ代表我们的激活函数,一般是sigmoid
MSE下的代价函数:
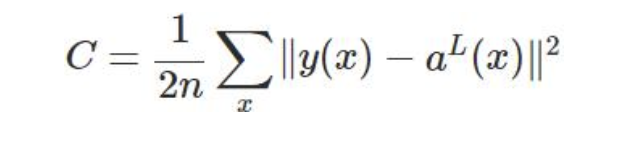
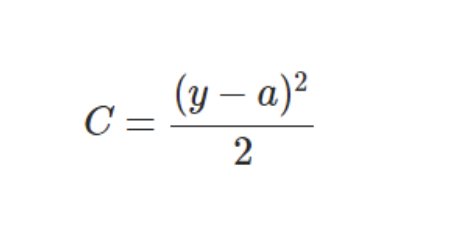
以偏置b的梯度计算为例,推导出交叉熵代价函数:
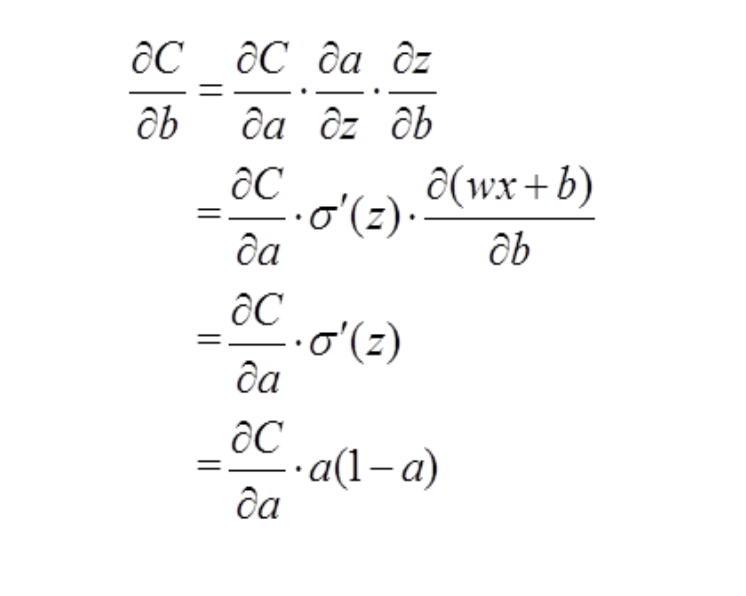
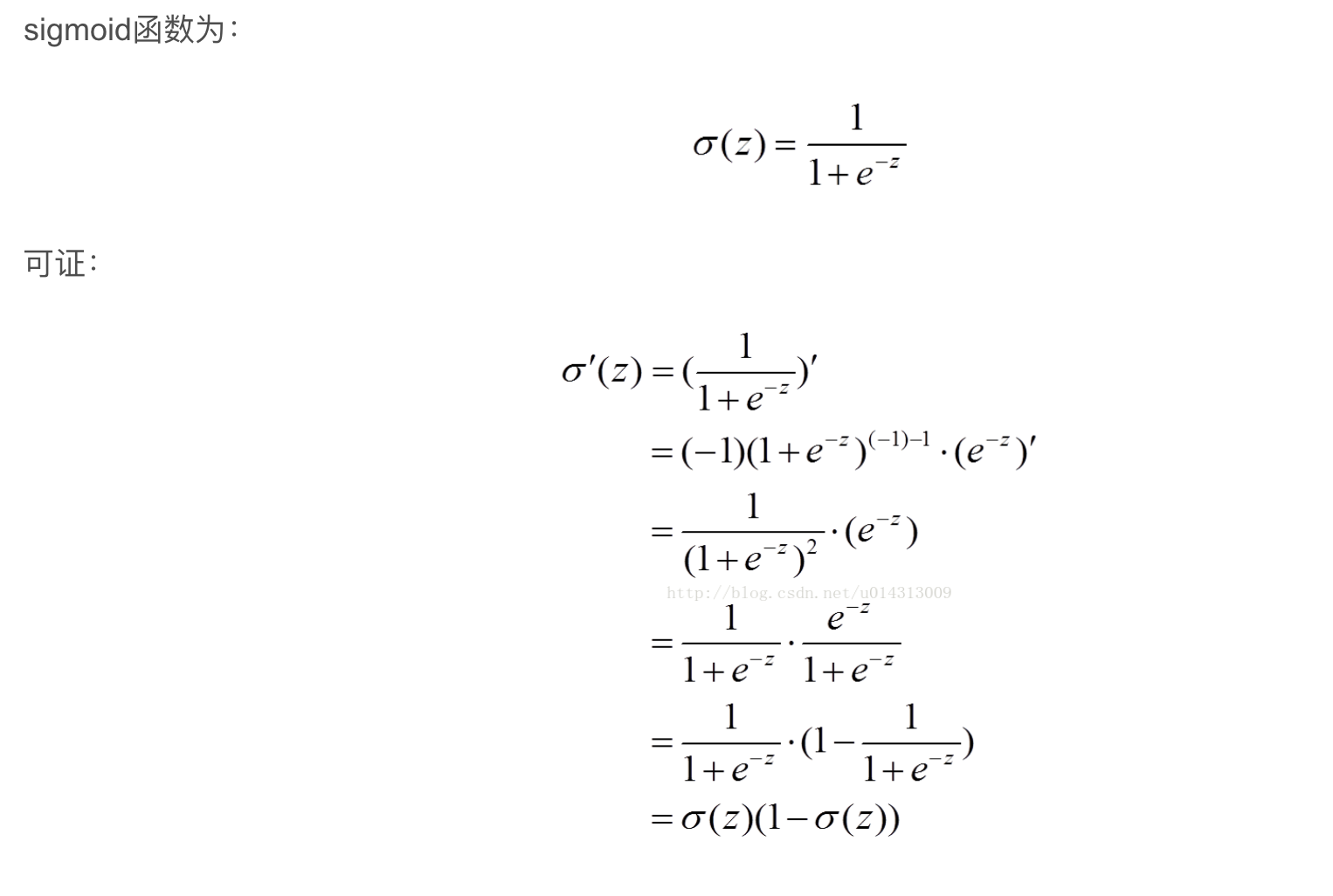
有二次代价函数:
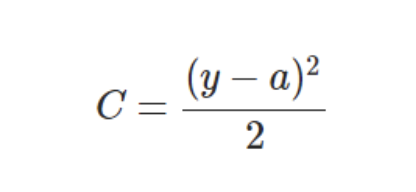
对二次代价函数求偏导有:
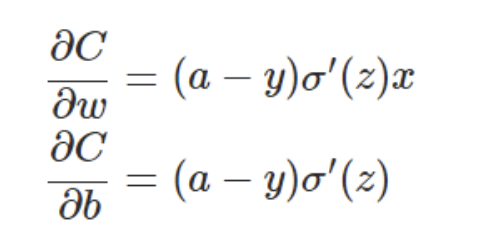

选取交叉熵作为cost function
由上面的推导可以看出,若使用MSE作为cost function,即:
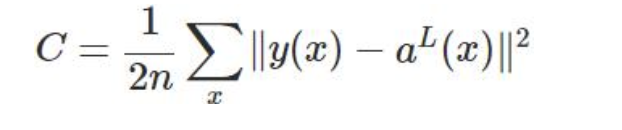
则会有推导(这里z=wx+b因为神经元之间关系就是线性的)
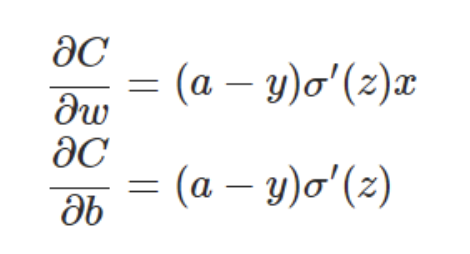
那么根据sigmoid的图表来看,当接近极值时斜率会降低,更新的速度就会降低
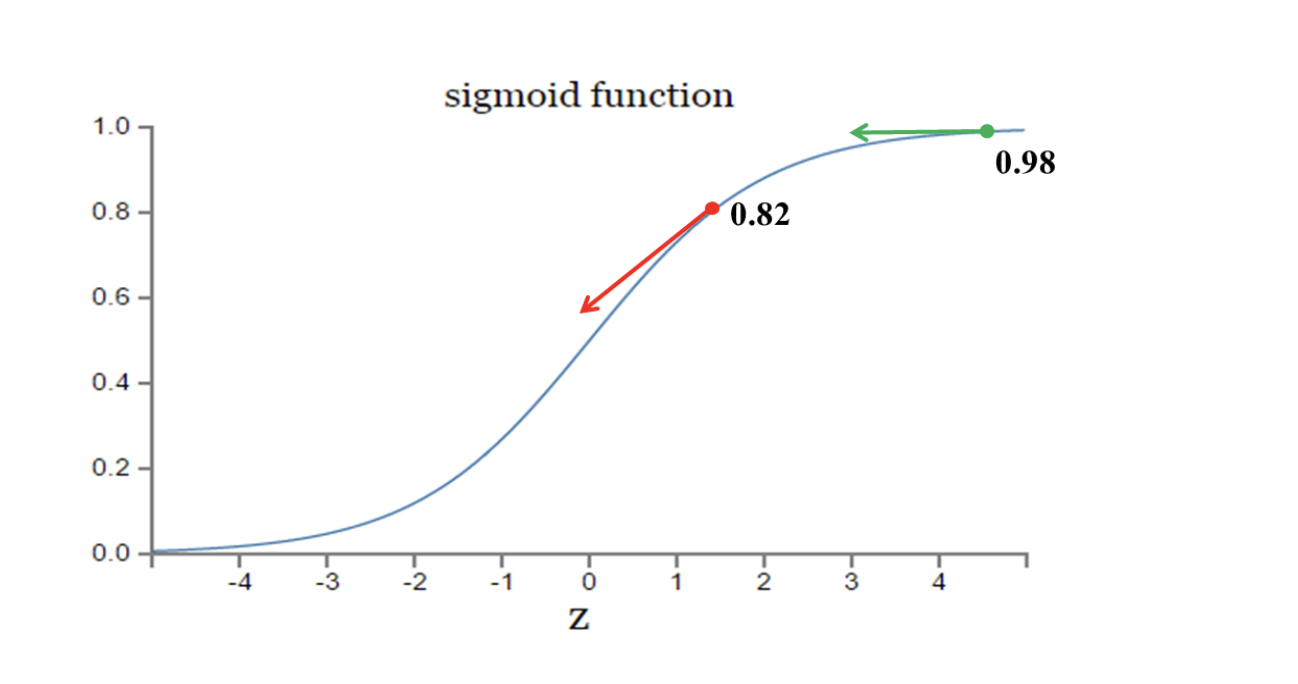
所以不能用MSE作为cost function
逻辑回归推导
逻辑回归也满足伯努利分布,所以他的本质就是交叉熵-----参见交叉熵推导1
h()作为目标函数,选取sigmoid函数作为激活函数g(),那么就有h(θ) = g(z), 那么这里面的z是线性关系,也就是linear function的结果作为z,最后输出一个[0,1]范围内的概率值,有h(θ) = g(wx+b)。
跟交叉熵类似。不选择MSE作为cost function的原因是我们需要找到一个值域在[0,1]且满足分类要求的函数,sigmoid正好合适。
而逻辑回归就是用线性回归预测的连续值通过sigmoid转换成0,1分类
别的
sigmoid函数实质为softmax函数的特殊情况
sigmoid函数用于多分类且分类独立
softmax用于多分类且分类互斥
参考资料
blog.csdn.net/tsyccnh/art…
zhuanlan.zhihu.com/p/44591359
blog.csdn.net/u014313009/…
sigmoid函数来源 论文http://www.win-vector.com/dfiles/LogisticRegressionMaxEnt.pdf
blog.csdn.net/weixin_3827…