理论基础

N-gram是自然语言处理中常见的一种语言模型。本节将介绍N-gram相关的理论基础知识。

概念介绍

假设你对天猫精灵说了一句话，天猫精灵经过语音识别后得到了三种可能的文本，分别是：“我爱中国”，“我爱钟国”，“我爱种果”。那么哪个文本是你最可能想表达的呢？

一般我们可以采用统计的方法，在一个语料库中，分别对“我爱中国”、“我爱钟国”、“我爱种果”这三句话进行统计。假设“我爱中国”出现的次数为 $N_1$ ；“我爱钟国”出现的次数为 $N_2$ ；“我爱种果”出现的次数是 $N_3$ ；整个语料库的句子数为 $N_0$ ；那么我们只需要比较三个句子在语料库中出现的概率 $\frac{N_1}{N_0}$ 、 $\frac{N_2}{N_0}$ 、 $\frac{N_3}{N_0}$ ，并取概率最大的一个句子。但这里存在一个问题，就是语料库规模有限而语言灵活多变。很有可能一个稍微长一点的句子，比如“我爱中国的大好河山”，语料库中就没有，那么模型判定出现的概率就是0，由于此种情况太容易出现，甚至有时候改动一个字都会导致该句子未在语料库中出现，故即使增加平滑策略，效果也不会太好。显然这种统计方法不是那么的好。

上述的方法采用的是纵向统计方法，主要是针对语料库，在句子粒度进行统计。我们不妨试一下横向统计方法，以字的粒度进行考虑。

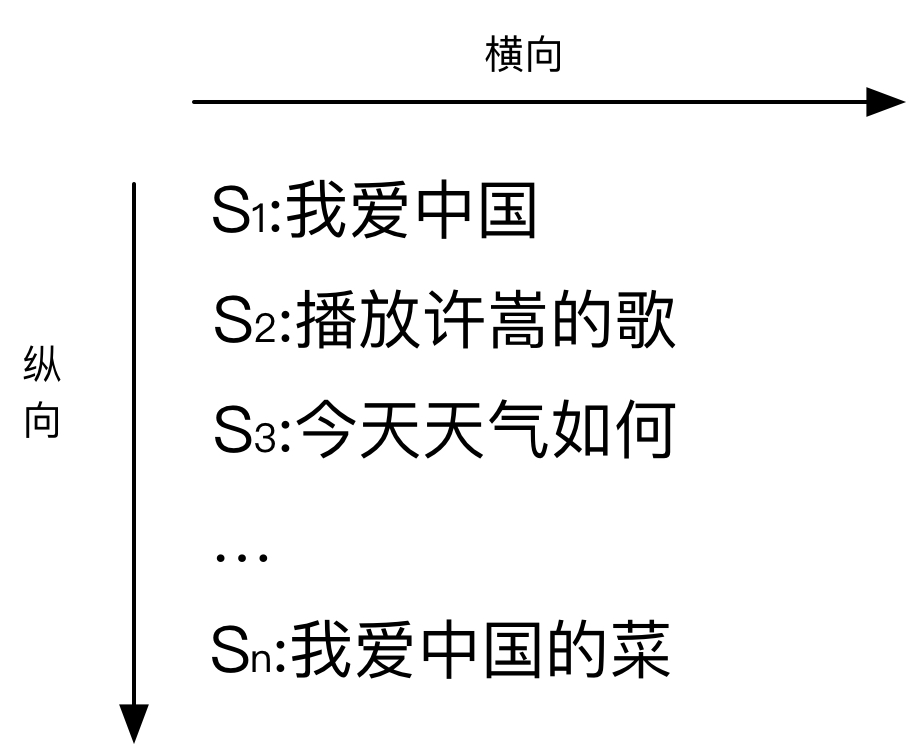
从横向角度出发，我们这样考虑“我爱中国”这句话出现的概率。先考虑“我”出现在句子第一个位置的概率，即 $P(“我”|BEGIN)$ ，其中“BEGIN”为句首的标识符。接下来再考虑当第一个字是“我”的时候，第二个字是“爱”的概率 $P(爱|我)$ ，依次类推，得到下面的链式公式：

P(我爱中国)=P(我|BEGIN)P(爱|我)P(中|我,爱)P(国|我,爱,中)

这个公式乍一眼看上去是没有问题。但是我们发现 $P(国|我,爱,中)=\cfrac{P(我,爱,中,国)}{P(我,爱,中)}$ ，可是 $P(我,爱,中,国)$ 本来就是我们要求的值，这饶了一圈又绕回来了。

那如果我们简化一下模型，比如我们只考虑在前一个字出现的情况下，后一个字出现的概率。即将 $P(w_j|w_1,w_2,…,w_{j-1})$ 转化为 $P(w_j|w_{j-1})$ ，这样简化的方式，我们就称作bi-gram。显而易见，bi-gram就是一种一阶马尔科夫链。这类的语言模型就可以称为n元语法(N-gram)。当n=1时，即第i个词 $w_i$ 独立于历史，不依赖上下文，一元文法就称作uni-gram。当n=3时，即第i个词 $w_i$ 仅根据其前两个历史词 $w_{i-2},w_{i-1}$ 有关，三元文法可以认为是二阶马尔科夫链，称作tri-gram。

模型推导

对于N元语法模型，我们考虑第n个词出现的概率只依赖于前N-1个词的概率，故该句子的概率分布：

\begin{eqnarray}P(s)&=&P(w_1,w_2,…w_n)\
&=&P(w_1|c^{w_0}_{w_{-n+2}})P(w_2|c^{w_1}_{w_{-n+3}})…P(w_i|c^{w_{i-1}}_{w_{i-n+1}})
\end{eqnarray}

其中，我们认为 $c^{w_0}_{w_{-n+2}}$ 为句首符号begin of sequence，即 $<BOS>$ ，并且取 $w_{i+1}$ 为句尾符号end of sequence，即 $<EOS>$ 。 $c^{w_{i-1}}_{w_{i-n+1}}$ 表示第 $w_i$ 个词到第 $w_{i-n+1}$ 个词的历史序列。根据最大似然估计，我们可以得到： $P(w_i|c^{w_{i-1}}_{w_{i-n+1}})=\frac{N(c^{w_i}_{w_{i-n+1}})}{N(c^{w_{i-1}}_{w_{i-n+1}}）}$

对于1元语法模型uni-gram，句子的概率分布: $P(s)=P(w_0)P(w_1)P(w_2)…P(w_i)P(w_{i+1})$

对于2元语法模型bi-gram，句子的概率分布: $P(s)=P(w_1|w_0)P(w_2|w_1)…P(w_i|w_{i-1})P(w_{i+1}|w_i)$

对于3元语法模型tri-gram，句子的概率分布: $P(s)=P(w_1|w_0,w_{-1})P(w_2|w_1,w_0)…P(w_i|w_{i-1}w_{i-2})P(w_{i+1}|w_i,w_{i-1})$

实例讲解

接下来，我会有一个简单的例子，帮助大家充分理解上述讲的过程。

假设语料库中有五个句子，分别是：

1、我爱中国大好河山

2、我喜欢中华料理

3、果农爱种果

4、我爱中彩票去外国

5、中国真好

当天猫精灵听到wo-ai-zhong-guo后，我们采用bi-gram模型来计算语句是“我爱中国”的概率，根据bi-gram模型：

P(我爱中国)=P(我|<BOS>)P(爱|我)P(中|爱)P(国|中)P(<EOS>|国)

其中:

P(我|<BOS>)=\frac{N(<BOS>,我)}{N(<BOS>)}=\frac{3}{5}

P(<EOS>|国)=\frac{N(国,<EOS>)}{N(国)}=\frac{1}{3}

所以：

P(我爱中国)=\frac{3}{5}\times\frac{2}{3}\times\frac{2}{3}\times\frac{2}{4}\times\frac{1}{3}=\frac{2}{45}

进阶优化

由于上述的模型是概率连乘，故同样会有一项为0，整项为0的情况。故我们需要采用平滑技术。一般的平滑策略就是“加1法”；即假设每个N元语法 $c^{w_i}_{w_{i-n+1}}$ 出现的次数比实际出现次数多一次。比如“你好”在上面的例子中， $P(你|<BOS>)$ 会从 $\frac{0}{5}$ 调整到 $\frac{1}{6}$ 。

工程实现

代码中Ngram为N-gram模型，具体代码如下。代码通过从国外的图书网站gutenberg中，选择一本书作为语料库，并使用n-gram模型，根据给定的开头词，自动生成一句话。

代码

# -*- coding: utf-8 -*-
"""
Created on Tue Sep 18 15:17:31 2018

@author: huangzhaolong
"""

import urllib.request
import gzip
import re


class spyder(object):
    def __init__(self):
        
        books = {'Pride and Prejudice': '1342',
         'Huckleberry Fin': '76',
         'Sherlock Holmes': '1661'}
        self.books = books
        
        url_template = 'https://www.gutenberg.org/cache/epub/%s/pg%s.txt'
        self.url_template = url_template
        
    def getUrlContent(self,book):
        '''
        根据url抓取内容进行解析
        '''
        url_template = self.url_template
        response = urllib.request.urlopen(url_template % (book, book))
        html = response.read()
        try:
            txt = gzip.decompress(html).decode(encoding="utf-8", errors="ignore")
        except:
            txt = html.decode(encoding="utf-8", errors="ignore")
        response.close()
        return txt

    def crawl(self,book):
        bookid = self.books[book]
        txt = self.getUrlContent(bookid)
        print ("文本总共长：",len(txt), ',前30个字符是：', txt[:30], '...')
        return txt


class Ngram(object):
    def __init__(self):
        #初始化Ngram中N的取值
        gram_N = [1,2,3,4,5]
        self.gram_N=gram_N
        #gram_list的每个元素是一个dict，这个dict包含了该Ngram下的gram和次数
        gram_list = [[] for i in gram_N]
        self.gram_list = gram_list
        
    def get_txt(self,txt):
        '''
        将抓取的内容，拆分成各个word
        '''
        #对这个文本取单词,所有单词构成一个list，并且过滤掉所有空
        words = re.split('[^A-Za-z]+', txt.lower())
        words = list(filter(None, words)) 
        print ("文本中所有单词的个数：",len(words))
        return words
    
    def generate_ngram(self, txt):
        '''
        将抓取的内容，存成gram_list
        gram_list里的每个元素是一个对应一个n的dict
        dict的key是ngram的gram,value是次数
        '''        
        words = self.get_txt(txt)
        
        gram_N = self.gram_N
        gram_list = self.gram_list
        gram_dict = [{} for i in gram_N]
        
        for n in gram_N:
            for i in range(len(words)-n+1):
                word_group = tuple(words[i:i+n])
                if word_group in gram_dict[n-1].keys():
                    gram_dict[n-1][word_group] += 1
                else:
                    gram_dict[n-1].update({word_group:1})
            '''
            将生成好的ngram的dict，根据gram出现的次数进行排序
            '''
            gram_list[n-1] = sorted(gram_dict[n-1].items(), key = lambda x:-x[1])
            print(n,"gram里排名前五的元素",gram_list[n-1][:5])
            
        self.gram_list = gram_list
        
    def generate_ngram_sentence(self, n=2, start_word = "you", length = 15):
        
        gram_list = self.gram_list
        
        print ("generating sentence...\n")
        '''
        根据其实词，生成ngram的前序序列
        例如如果是4gram，，起始词是"you"
        先根据2gram+'you'，找到'are'
        在根据3gram+'you','are'找到'not'
        最后得到前序输入'you','are','not'开始4gram生成下一个词
        '''
        current_sentence = []
        current_sentence.append(start_word)
        for i in range(n-2):
            current_word = tuple(current_sentence[-(i+1):])
            next_word = ""
            for element in gram_list[i+1]:
                if current_word == element[0][0:(i+1)]:
                    next_word = element[0][(i+1)]
                    break;
            if next_word == "" :
                break;
            current_sentence.append(next_word)
            
        '''
        根据前n-1个gram，预测下一个gram，即p(x_m|x_m-1...x_(m-n+1))
        '''
        for i in range(length):
            current_word = tuple(current_sentence[-(n-1):])
            next_word = ""
            for element in gram_list[n-1]:
                if current_word == element[0][0:n-1]:
                    next_word = element[0][n-1]
                    break;
            if next_word == "" :
                break;
            current_sentence.append(next_word)
                
        print("sentence:",' '.join(current_sentence))

        
if __name__=="__main__":
    #定义一个爬虫，去抓取相关的文本
    spy = spyder()
    txt = spy.crawl('Sherlock Holmes')
    #对文本进行ngram
    ngram = Ngram()
    ngram.generate_ngram(txt)
    #自动生成gram
    n = 3
    start_word = "then"
    sentence_len = 20
    ngram.generate_ngram_sentence(n,start_word,sentence_len)

结果

1 sentence: then i shall be happy to look at it earnestly drive like the devil he shouted first to gross hankey s in

自然语言处理系列之一：N元语法-ngram

理论基础

概念介绍

模型推导

实例讲解

进阶优化

相关应用

判断一个字符串是否合理

判断两个字符串的距离

工程实现

代码

结果