数据结构
排序
选择排序
每次选出最小的放左边。即使数组有序，也要进行比较
选择排序是不稳定的，比如：5 5 2
public int[] sort(int[] sourceArray) throwsException {
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
// 每轮需要比较的次数 N-i
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的下标
min = j;
}
}
// 将找到的最小值和 i 位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
return arr;
}
冒泡排序
交换相邻逆序的元素，使最大的放到右边。若一轮中未发生交换，则数组已经有序
private static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
// 每一轮把最大的放到右边
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
插入排序
将当前元素插入到左侧已经排序的数组中，使得插入之后左侧数组依然有序
希尔排序
数组划分为多个小的部分（非连续，根据步长划分），每个部分进行插入排序；不断缩小步长，直至步长为 1
为什么优于直接插入排序？
答：希尔排序一次移动可以跨越不止一个元素。比如对于序列 345672，34567 已经有序，对于 2 来说，直接插入排序（每次往左移一格）需要比较 5 次，而希尔排序（每次往前移动多格）比较次数小于 5 次
归并排序
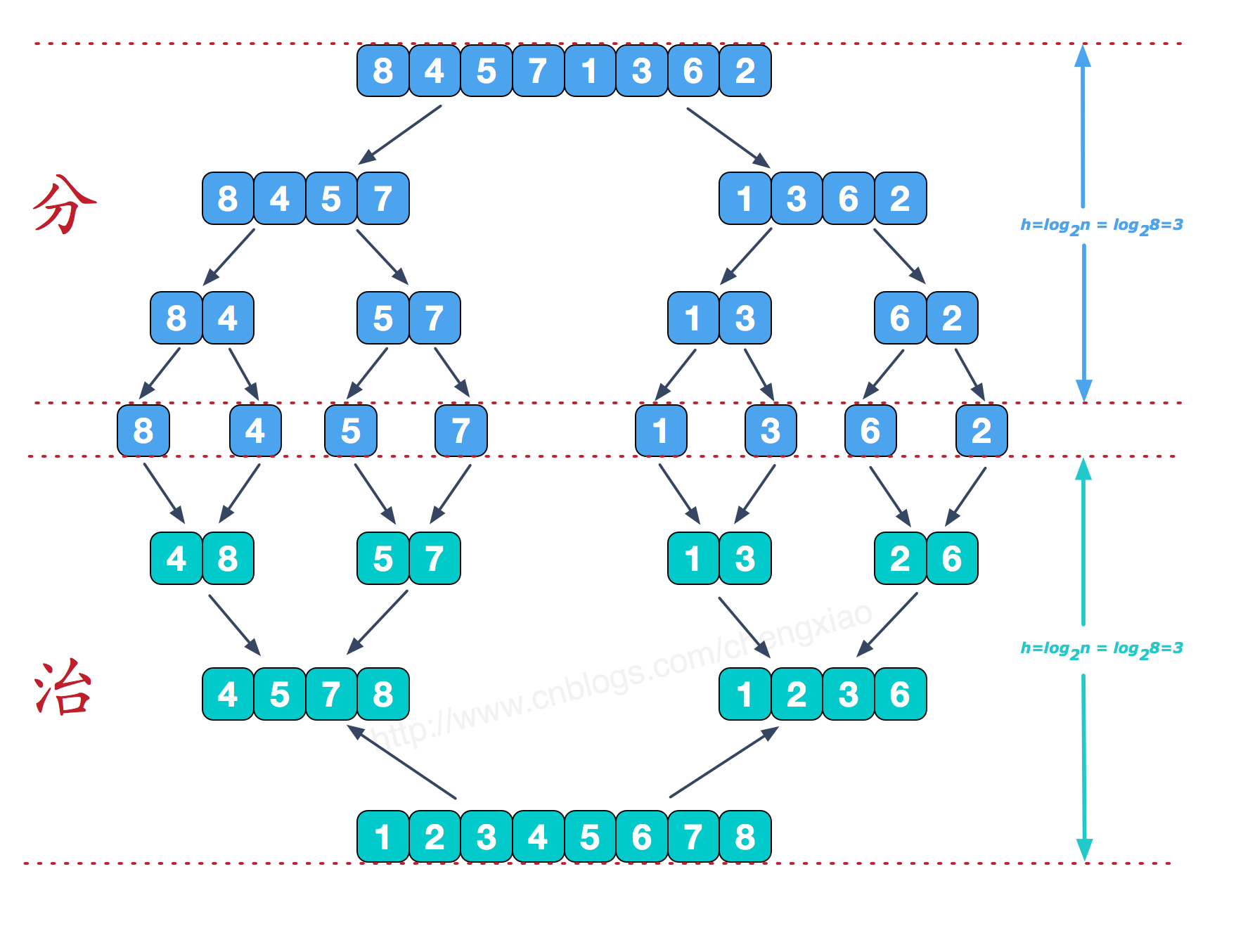
代码：
快速排序
同样分治。
最坏情况：数组升序，pivot为最小值，那么第一次partition只能把数组分为 1 个和 n - 1 个，这样需要 n 层二叉树
最好情况：每次左右数组数量一样多
代码：
private static void quickSort(int[] nums, int l,int r) {
if (l < r) {
int pos = partition(nums, l, r);
quickSort(nums, l, pos - 1);
quickSort(nums, pos + 1, r);
}
}
private static int partition(int[] nums, int l, intr) {
Random rand = new Random();
int randIndex = rand.nextInt(r - l + 1) + l;
int pivot = nums[randIndex];
swap(nums, randIndex, l);
while (l < r) {
while (r > l && nums[r] > pivot) {
r--;
}
nums[l] = nums[r];
while (l < r && nums[l] <= pivot) {
l++;
}
nums[r] = nums[l];
}
nums[l] = pivot;
return l;
}
堆排序
将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余 n-1 个元素重新构造成一个堆，这样会得到 n 个元素的次小值。如此反复执行，便能得到一个有序序列了
注：从最后一个非叶子结点开始（第一个非叶子结点arr.length() / 2 - 1）调整堆
桶排序、计数排序、基数排序
基数排序和计数排序都可以看作是桶排序
- 计数排序本质上是一种特殊的桶排序，当桶的个数取最大(maxV - minV + 1)的时候，就变成了计数排序
- 基数排序也是一种桶排序。桶排序是按值区间划分桶，基数排序是按数位来划分；基数排序可以看做是多轮桶排序，每个数位上都进行一轮桶排序 blog.csdn.net/qq_25026989…
图片来自：www.cnblogs.com/onepixel/ar…
————————
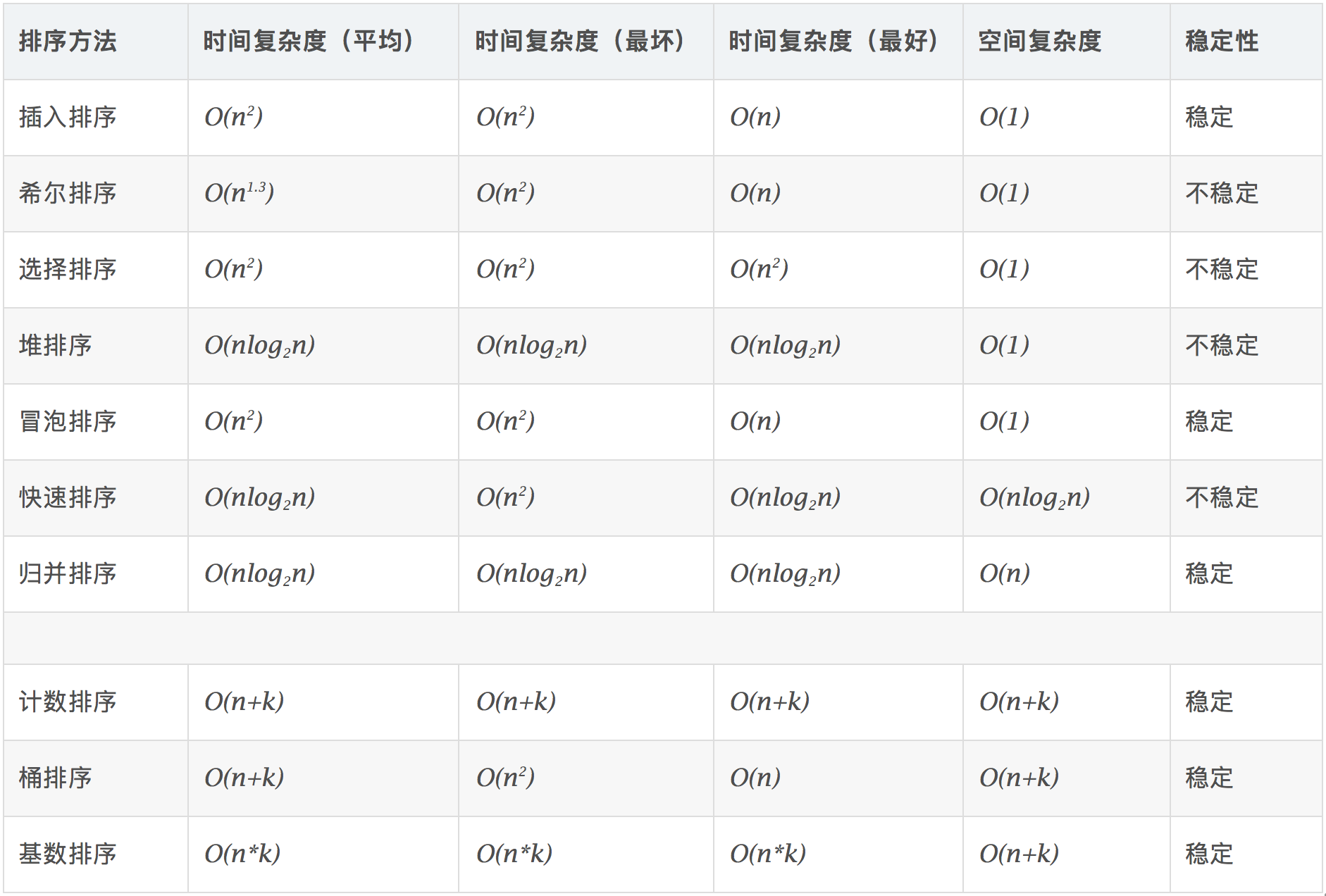
拓扑排序
拓扑排序是将有向无环图 G 的所有顶点排成一个线性序列，用队列实现
AOE & AOV 网
AOE 网中的最长路径被称为关键路径，即最短工期。可用动态规划求
并查集
```Java
/** 查找并返回根结点编号 */
static int find(int[] parent, int i) {
// 如果是根结点，则返回根结点编号
if (parent[i] == -1) {
return i;
}
// 否则，递归查找父亲结点是不是根结点
return find(parent, parent[i]);
}
/** 合并 */
static void union(int[] parent, int x,int y) {
int xset = find(parent, x);
int yset = find(parent, y);
// 若根结点不相同，则让 x 集合的根结点指向 y 集合的根结点，这样他们就指向相同的根结点了
if (xset != yset) {
parent[xset] = yset;
}
}
```
具体应用看搜索专题的“朋友圈”题目
树
非递归中序遍历
在中序遍历中如果要输出一个节点，要么该节点没有左孩子，要么该节点的左子树已经全部输出。
从根结点开始，循环将左孩子入栈直到左子树为空，输出栈顶元素，并把右孩子入栈。继续循环把左孩子入栈...（输出的条件就是左子树为空）
代码：paste.ubuntu.com/p/68Wk4R7jP…
非递归前序遍历
根结点入栈，并输出。当该节点的右孩子节点不为空时，将节点压入栈；当左孩子节点不为空时，将左孩子节点压入栈，输出栈顶元素（先进右节点是因为栈是先进后出）。再将左孩子节点的右孩子结点入栈，重复上面的操作...
多叉树转二叉树
孩子兄弟表示法（右兄弟结点转为右孩子结点）
霍夫曼树
带权路径长度最短的二叉树
完全二叉树
从左到右依次填充
满二叉树：定义有歧义
二叉查找树
- 查找失败的地方就是插入的地方
- 删除
- 叶子结点：直接删除
- 非叶子结点：用前驱结点（左子树中的最大结点）或后继结点覆盖
- 中序遍历，结果有序
平衡二叉树 & 红黑树
红黑树是一种自平衡二叉搜索树。能够保证插、删、查的最坏情况不会降到
- 节点是红色或黑色
- 根节点是黑色
- 每个叶子节点都是黑色的空节点（NIL节点）
- 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
- 平衡二叉树的插入可能需要左旋、右旋。比二分查找的优点是，改变树结构（插入与删除结点）不需要移动大段的内存数据
- AVL 树比红黑树提供更快的查找，因为它是更严格的平衡
- 红黑树的插入和删除操作比 AVL 树的旋转次数较少（任何不平衡都会在三次旋转之内解决）
- AVL 树存储每个节点的平衡因子或高度，因此要用整数存储，而红黑树只需存储颜色，1 位就行
blog.csdn.net/mmshixing/a…
下面的树也是平衡二叉树：
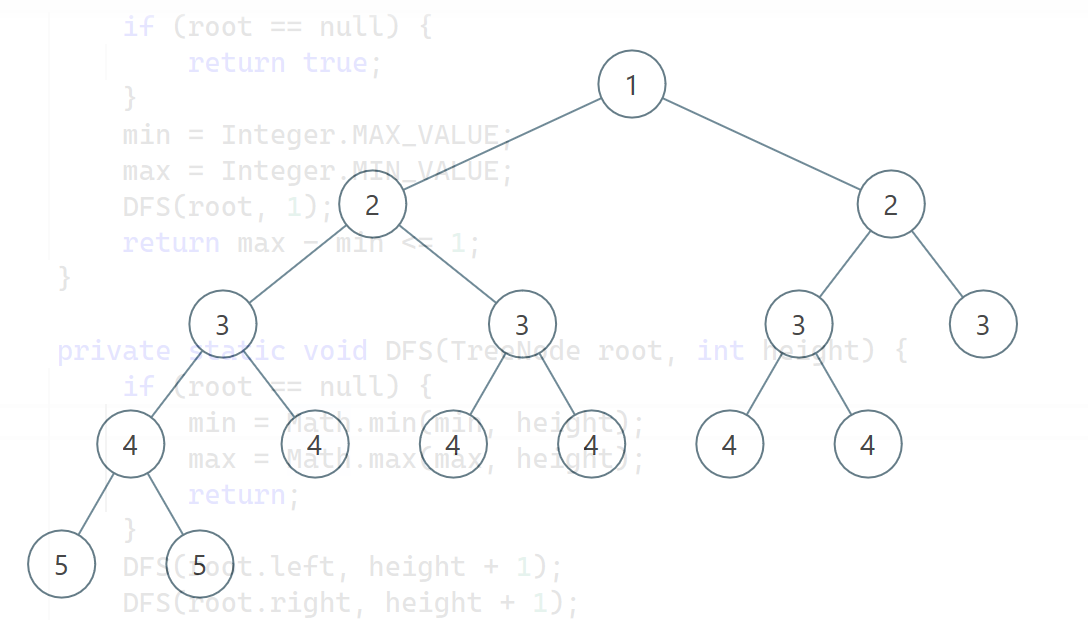
- 简单说，搜索的次数远远大于插入和删除，那么选择 AVL 树，如果搜索，插入删除次数几乎差不多，应该选择红黑树。
线索二叉树
插入和删除更方便
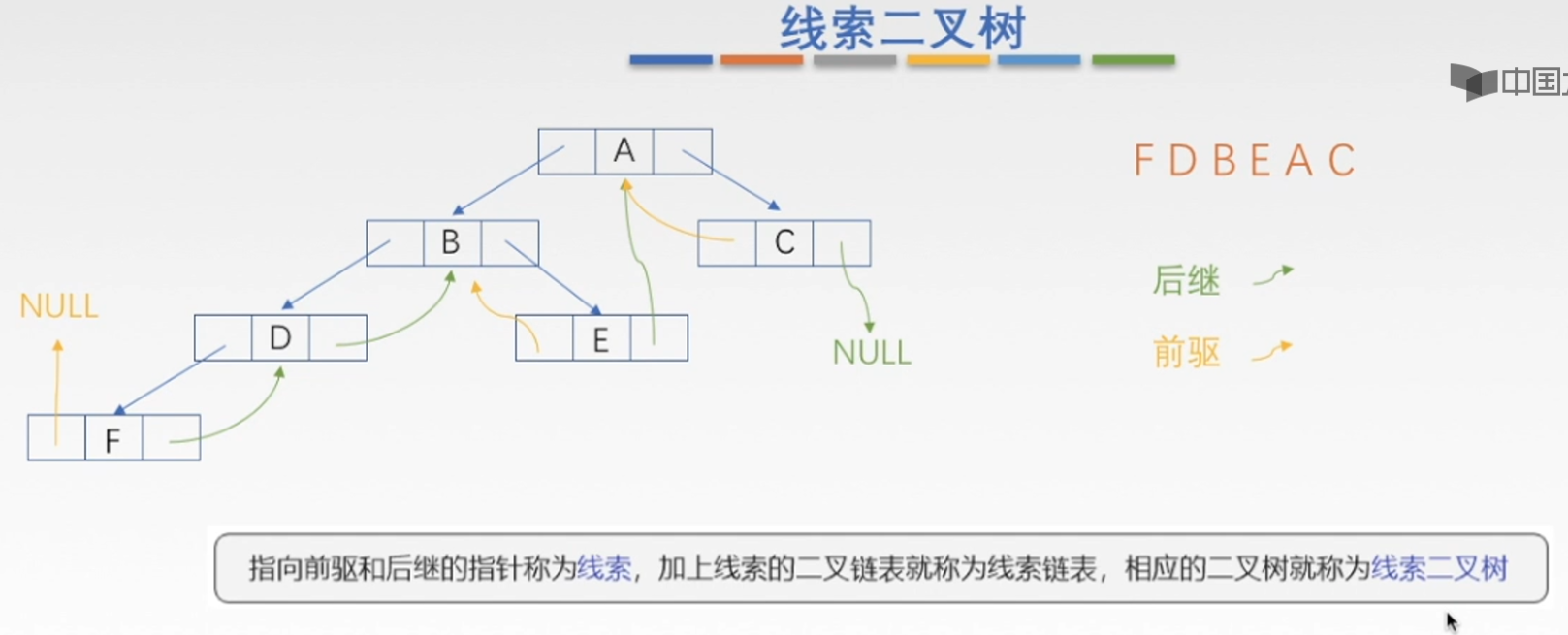
B 树、B+ 树
B 树又叫平衡多路查找树
B 树适用于读写相对大的数据块的存储系统，例如磁盘。B 树减少定位记录时所经历的中间过程，从而加快存取速度。B 树这种数据结构常被应用在数据库（尽量减少磁盘 IO 就可以显著的提升数据的查询速度）和文件系统的实现上。why？
- B+ 树的关键字和子树指针一一对应
- B+ 树中每个父结点的元素，都是相应子节点的最大元素
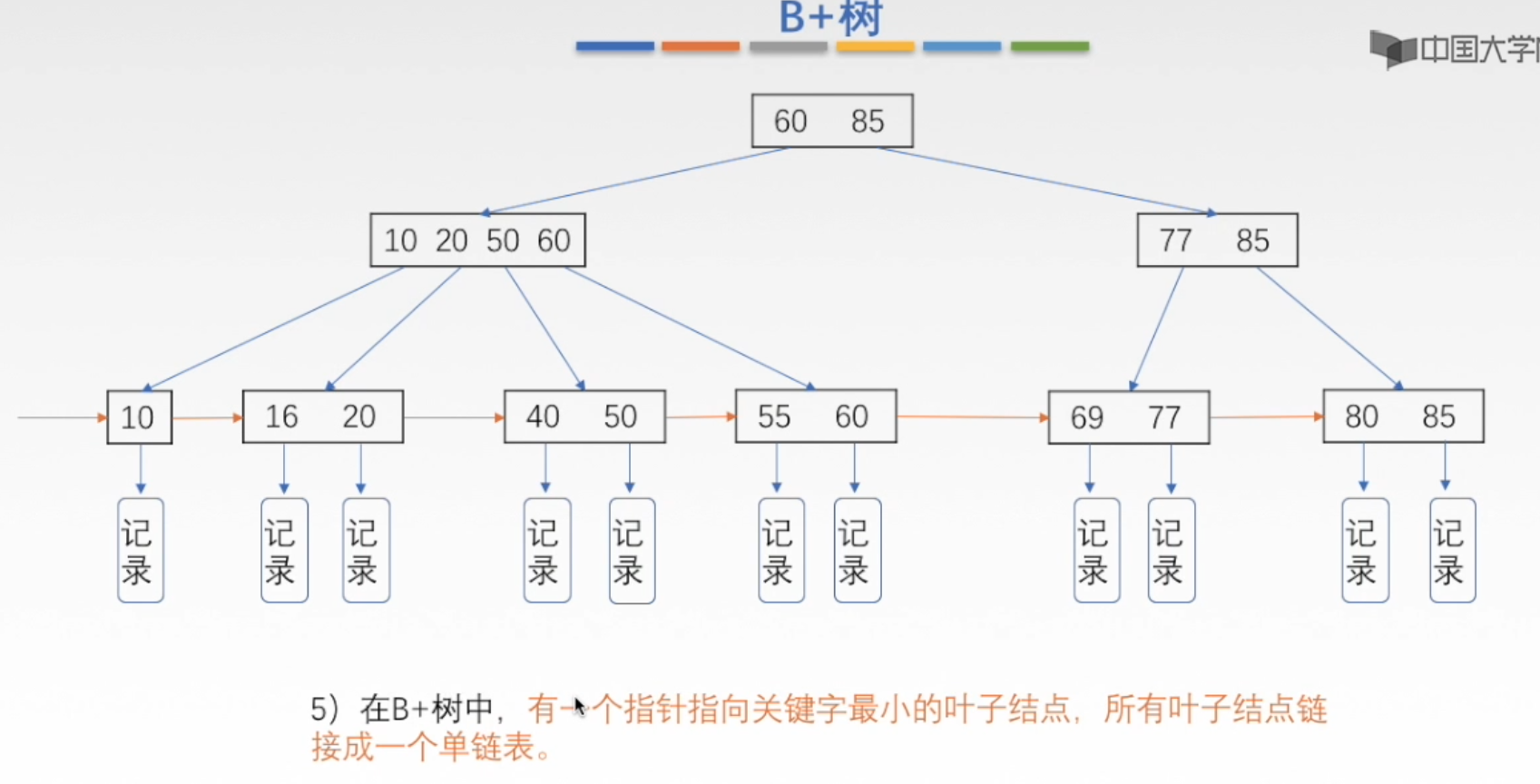
- B+ 树的内部结点并没有指向关键字具体信息的指针，仅叶结点包含具体信息，所有非叶结点只含有对应子树的最大关键字和指向该子树的指针。
- 综合起来，B+ 树相比 B 树的优势有三个：
- IO 次数更少（B+ 树中间节点没有卫星数据，只有索引，而 B 树每个结点中的每个关键字都有卫星数据；这就意味着同样的大小的磁盘页可以容纳更多节点元素，在相同的数据量下，B+ 树更加“矮胖”，IO 操作更少）
查询性能稳定（B+ 树全在叶子节点，B 树可能在根结点，可能在其他结点）- 范围查询简便（因为叶子结点之间有指针相连，所以 B+ 树也可以顺序查找）
⭐
出自 CSDN
