1 背景
理论中对图像的处理通常分为三种,与一些简单的计算相关的低层视觉(图像统计与简单计算,如直方图、滤波、纹理等),与一些已知人眼视觉特性相关的中层视觉(图像理解,如梯度、匹配跟踪、图像特征等),与人眼视觉特性、思维方式高度相关的高级视觉(图像理解,如分类、检测、基于语义的处理等)。
其中,图像特征是一种老生常谈的图像信息,早期的方法如梯度提取算子、图像的局部直方图等都可以作为图像的局部特征去使用。而近年来被广泛关注的卷积神经网络等方法,也是通过卷积等网络框架去得到一层(或多层)特定大小的特征图,以此作为图像的特征,实现分类等特定的目的。
本文将聚焦于传统图像处理中的局部特征计算,并介绍一种图像局部特征的应用——全景图像拼接。
2 局部特征提取中存在的问题
图像特征信息是图像中的重要信息,在图像匹配、图像拼接等方面有不可替代的作用,如果不利用图像特征,我们几乎找不出其他行之有效的方法去解决图像匹配等问题,如下图所示。
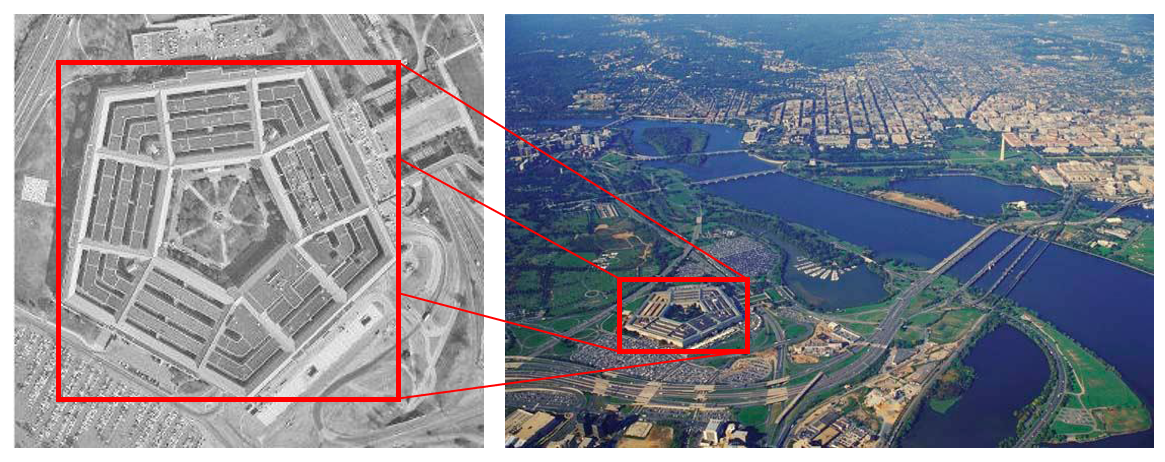
通过直接的视觉判别,我们很容易匹配出两幅图像相同的地方,但是如何让计算机自动、流程化地区实现图像匹配,这就需要提取图像的特征并实现匹配。
但是图像的特征信息并不是那么容易就可以得到的,如果不参考相关的研究自己琢磨怎么去提取特征,那么迎面而来的问题如下
场景1:光照的大幅变化

场景2:视场角、距离的大幅变化

对于场景1,光照的变化,大家肯定还能分辨出场景中的相同部分,但对场景2,绝大多数人甚至没法进行直观视觉上的区域匹配。这个问题就是有这么离谱,人都分辨不出来,还能交给计算机去完成吗,答案是可以,结果如下。

我们可以总结一下,我们需要什么样的特征,或者说一个好的特征应该满足哪些条件。
1.几何不变:不因几何形变而改变

2.光照不变:不因光照的改变而改变

3.可重复与准确度:重复提取特征,结果不会发生改变,同时准确度高
4.数量足够:需要较多数量的点来覆盖一块区域
5.特征性:每个特征都要独一无二,有明显特点利于区分
由此,我们已经明确了何为图像特征,以及图像特征最好能够具有的性质。
3 Harris角点检测
目的:
- 可重复检测
- 精确定位
- 包含图像的高频信息
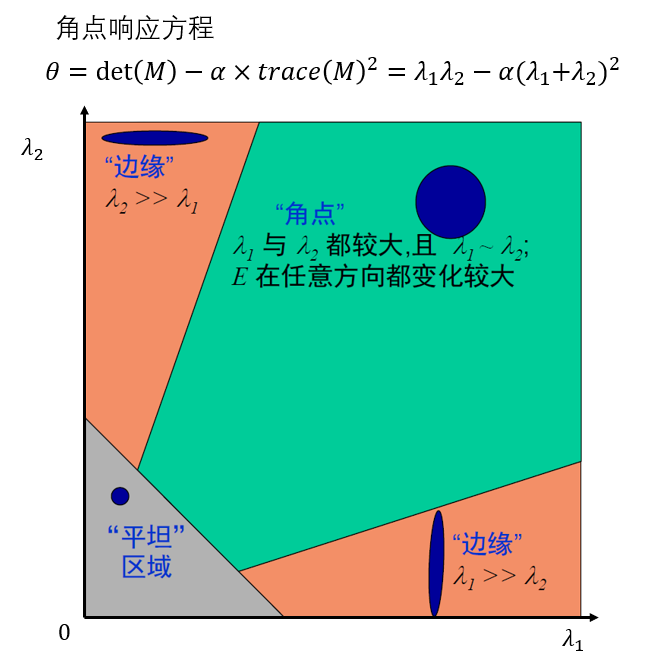
本质:寻找图像的二维信号变化,在角点区域附近,图像的梯度有两个或更多的变化方向。
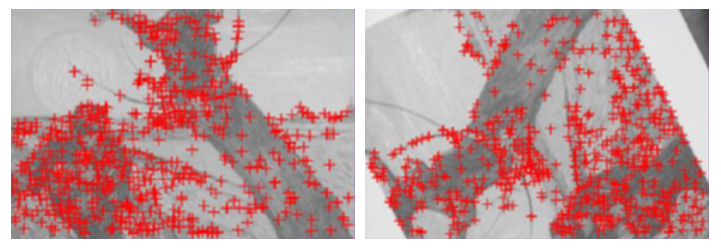
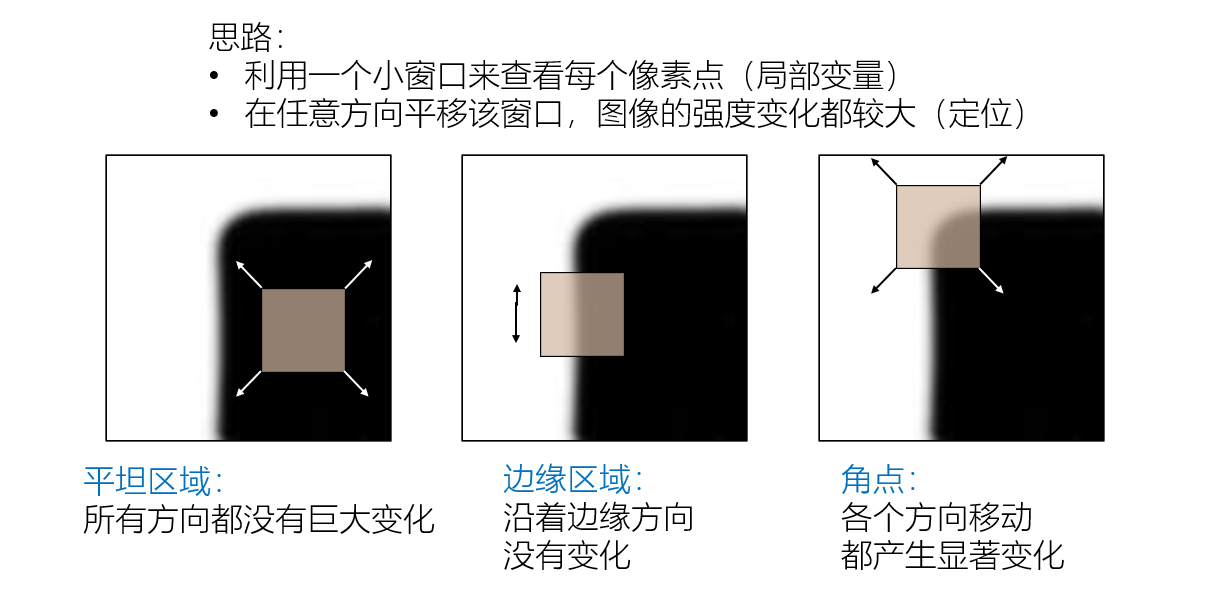
而角点有如下的数理规律:
对于平坦区域,在水平和竖直方向上的梯度小;对于边缘区域,在水平和竖直两个方向上有一者梯度大,一者梯度小;对于角点,则在两个方向上都有较大的梯度。下图较形象地描述了三者的区别。
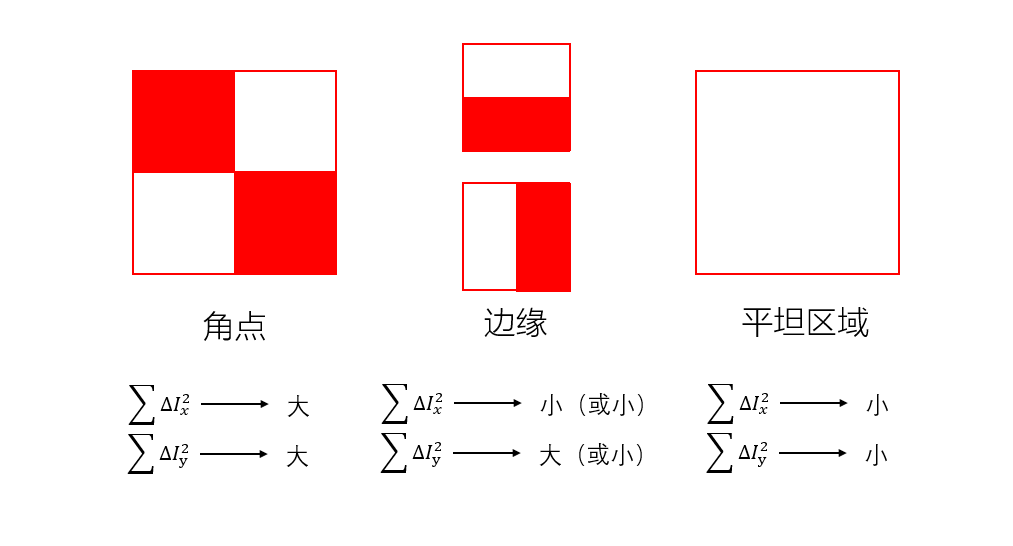
3.1 Harris角点检测的数学表达
将图像平移产生灰度变化
,如下:
由泰勒展开,得
则
其中项可以被近似认为是0,因此
二次项展开
该式用矩阵来表示为:
此表达式即为
在编程的时候,我们将M当作一个2x2的矩阵,可以由图像的梯度计算而来
观察一下上式,它表明:
- 主要梯度变化方向沿着x方向或y方向
- 如果任意一个
接近于0,那么这就不是一个角,因此只有两个
都较大才是角点。
3.2 Harris角点检测示例
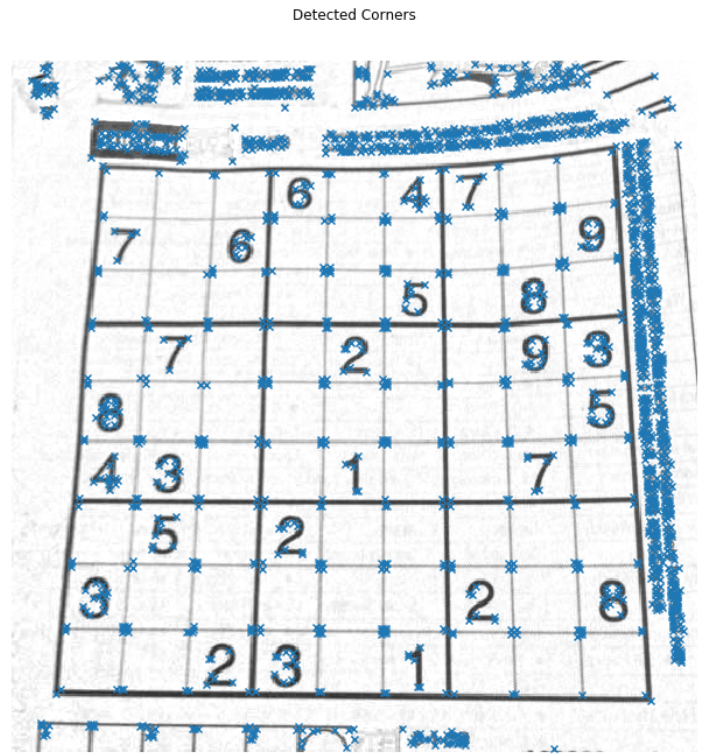
对于一幅输入图像,其经过非极大值抑制的Harris角点响应图如下。(代码部分详见代码实战部分与实施例)


其中,亮点与红点区域即为Harris角点计算所得的角点区域。
Harris角点检测可以保证图像特征的平移不变性、旋转不变性、强度(光照)不变性,但缺陷在于无法保证尺度不变(缩放不变),因此对于不同的窗口大小,能够检测出的角点有所不同。这就导致了特征因拍摄距离的变化而发生变化,无法做到特征的稳定性。
4 方向梯度直方图(Histogram of Oriented Gradients, HOG)
目标:
- 寻找一组稳定的特征用以分辨物体(主要是人)
- 主要用于图像的整体描述(图片中的滑动窗口)
难点:
- 形状与外貌变化太广
- 不同的照明条件下,背景过于庞杂
- 实时处理速度有所限制
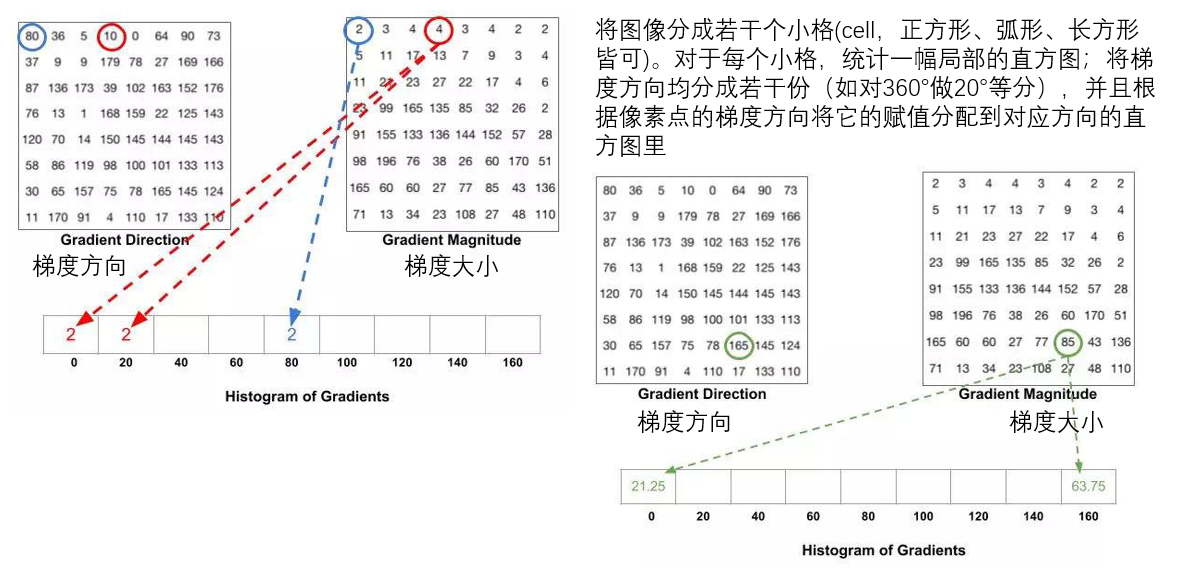
HOG背后的原理涉及数学的部分较少,我们可以用过程形象地说其作用原理。
5 图像特征的应用:相机中全景图像的计算成像


此处的合成图像过渡不平滑,是因为成像过程中镜头的进光量等因素的变化所导致的,解决该问题有许多方法,如图像金字塔融合、加权融合等,这不是本文重点。
6 代码实战部分
# Python 3.6
# panorama.py
import numpy as np
from skimage import filters
from skimage.feature import corner_peaks
from skimage.util.shape import view_as_blocks
from scipy.spatial.distance import cdist
from scipy.ndimage.filters import convolve
from utils import pad, unpad, get_output_space, warp_image
def harris_corners(img, window_size=3, k=0.04):
"""
计算图像的Harris角点值,其计算公式如下:
R=Det(M)-k(Trace(M)^2).
提示:
你可以利用卷积函数 scipy.ndimage.filters.convolve。
参数:
img: 形状为 (H, W)的灰度图
window_size: kernel的尺寸
k: 敏感度调节因子
返回值:
response: 图像的角点响应值 (H, W)
"""
#img = img[:,:,0] #如果29行报错,请把28行的img = [:,:,0]的注释取消
H, W = img.shape
window = np.ones((window_size, window_size))
response = np.zeros((H, W))
dx = filters.sobel_v(img)
dy = filters.sobel_h(img)
### YOUR CODE HERE
#M = np.ones((H, W,2, 2))
#padded_dx = np.pad(dx, int((window_size-1)/2), mode='edge')
#padded_dy = np.pad(dy, int((window_size-1)/2), mode='edge')
#for i in range(H):
#for j in range(W):
#M[i, j, :, :] = np.array([[sum(sum(b) for b in (padded_dx[i:i+2, j:j+2]*padded_dx[i:i+2, j:j+2])),sum(sum(b) for b in (padded_dx[i:i+2, j:j+2]*padded_dy[i:i+2, j:j+2]))],[sum(sum(b) for b in (padded_dx[i:i+2, j:j+2]*padded_dy[i:i+2, j:j+2])),sum(sum(b) for b in (padded_dy[i:i+2, j:j+2]*padded_dy[i:i+2, j:j+2]))]])
#for a in range(H):
#for b in range(W):
#response[a][b]=np.linalg.det(M[a][b])-k*(np.trace(M[a][b])**2)
dxx = dx * dx
dyy = dy * dy
dxy = dx * dy
mxx = convolve(dxx, window)
mxy = convolve(dxy, window)
myy = convolve(dyy, window)
for i in range(H):
for j in range(W):
M = np.array([[mxx[i, j], mxy[i, j]], [mxy[i, j], myy[i, j]]])
response[i, j] = np.linalg.det(M) - k * np.trace(M) ** 2
### END YOUR CODE
return response
def simple_descriptor(patch):
"""
将像素值分布进行标准正态化来描述这个小patch (标准正态分布的均值为0,标准差为1),
然后将它展开成一维的数组.
正态化的操作会使描述子对于光照变化更加robust.
提示:
如果分母为0,那就用1来代替.
Args:
patch: 尺寸为 (H, W)的灰度图像
Returns:
feature: 尺寸为 (H * W)的一维数组
"""
feature = []
### YOUR CODE HERE
patch = patch.reshape(-1)
mean = np.mean(patch)
delta = np.std(patch)
if delta > 0.0:
patch = (patch - mean) / delta
else:
patch = patch - mean
feature = list(patch)
### END YOUR CODE
return feature
def describe_keypoints(image, keypoints, desc_func, patch_size=16):
"""
Args:
image: 尺寸为 (H, W)的灰度图
keypoints: 二维数组,每一行都包含一个关键点 (y, x)。
desc_func: 特征描述函数,输入一张图,输出为它所对应的描述算子
patch_size: 每个特征点所对应的局部图像的尺寸。为了简化,这里将长宽设定成相同。
Returns:
desc: 描述各个特征点的特征向量
"""
image.astype(np.float32)
desc = []
for i, kp in enumerate(keypoints):
y, x = kp
patch = image[y-(patch_size//2):y+((patch_size+1)//2),
x-(patch_size//2):x+((patch_size+1)//2)]
desc.append(desc_func(patch))
return np.array(desc)
def match_descriptors(desc1, desc2, threshold=0.5):
"""
通过计算两点之间的欧氏距离来完成特征点的匹配. 现在,我们有两组特征向量。
从第一组中任选一个特征向量v1,计算它与第二组每个特征向量之间的距离,我们就得到了v1与其他特征向量之间的距离。
如果离v1最近的特征向量分别是v21,v22,那么,如果v1和v21的距离远小于v1和v22的距离,那么,我们认为v1和v21就是一组。
也就是说d(v1,v21)/d(v1,v22)需要小于某个阈值(threshold)。
据此,我们可以找出所有的匹配点。
提示:
Numpy 里的函数 np.sort, np.argmin, np.asarray 可能会对计算有帮助。
Args:
desc1: 形状为 (M, P)的数组,它的每一行都是一个描述子(尺寸为P),共有M个特征向量(M个特征点)。
desc2: 形状为 (N, P)的数组,它的每一行都是一个描述子(尺寸为P),共有N个特征向量(N个特征点)。
Returns:
matches: 尺寸为 (Q, 2) 的数组。它的每一行都是一组匹配的特征点序号(indices of one pair
of matching descriptors)。
"""
matches = []
N = desc1.shape[0]
dists = cdist(desc1, desc2) # 每个向量的欧式距离 N * N
### YOUR CODE HERE
#M = desc2.shape[1]
idx = np.argsort(dists, axis=1)
for i in range(N):
closed_dist = dists[i, idx[i, 0]]
second_dist = dists[i, idx[i, 1]]
if(closed_dist < threshold * second_dist):
matches.append([i, idx[i, 0]])
matches = np.array(matches)
### END YOUR CODE
return matches
def fit_affine_matrix(p1, p2):
""" 拟合 affine变换矩阵,使得 p2 * H = p1
提示:
你可以使用 np.linalg.lstsq 函数来求解这个问题.
Args:
p1: 尺寸为 (M, P) 的矩阵,每一行代表一个特征点的坐标
p2: 尺寸为 (M, P) 的矩阵,每一行代表一个特征点的坐标
Return:
H: 尺寸为 (P, P) 的矩阵,他将p2转换到p1。
"""
assert (p1.shape[0] == p2.shape[0])
p1 = pad(p1)
p2 = pad(p2)
### YOUR CODE HERE
H = np.linalg.lstsq(p2, p1)[0]
### END YOUR CODE
# 有时候由于噪声影响,会使得最后一列不是精确的[0, 0, 1],此时我们可以手动将它置为[0, 0, 1]
H[:,2] = np.array([0, 0, 1])
return H
def ransac(keypoints1, keypoints2, matches, n_iters=200, threshold=20):
"""
利用 RANSAC 来找到一组robust的affine变换
1. 随机选取若干组match点(对于affine变换,至少需要选取三组match,想想这是为什么?)
2. 计算affine的变换矩阵
3. 计算有效数据点(inliers)的数目
4. 记录有效点数目最大的那组参数
5. 根据所有的有效点,重新计算一遍变换矩阵
Args:
keypoints1: M1 x 2 矩阵,每一行都是一个像素点
keypoints2: M2 x 2 矩阵,每一行都是一个像素点
matches: N x 2 的矩阵,每一行都代表一组match
[keypoint1的序号, keypoint 2的序号]
n_iters: RANSAC算法要进行循环的次数。为了简化计算,这里将循环次数固定到了200。
(想想我们上课时候讲过如何确定循环次数?在不知道数据好坏的情况下,如何动态地改变循环次数?)
threshold: 有效数据点个数的阈值
提示:np.random.choice函数可能会有帮助
Returns:
H: 对于affine变换的一个robust的估计,它将 keypoints2 变换到了 keypoints 1
"""
# 保存match数组,避免对它直接改写
orig_matches = matches.copy()
matches = matches.copy()
N = matches.shape[0]
print(N)
n_samples = int(N * 0.2) #这里将n_samples的值与N联系起来。对于affine变换,你也可以将它固定到3.
matched1 = pad(keypoints1[matches[:,0]])
matched2 = pad(keypoints2[matches[:,1]])
max_inliers = np.zeros(N)
n_inliers = 0
# 开始对RANSAC 算法进行循环
### YOUR CODE HERE
for i in range(n_iters):
temp_max = np.zeros(N, dtype=np.int32)
temp_n = 0
idx = np.random.choice(N, n_samples, replace=False)
p1 = matched1[idx, :]
p2 = matched2[idx, :]
H = np.linalg.lstsq(p2, p1)[0]
H[:, 2] = np.array([0, 0, 1])
temp_max = np.linalg.norm(matched2.dot(H) - matched1, axis=1) ** 2 < threshold
temp_n = np.sum(temp_max)
if temp_n > n_inliers:
max_inliers = temp_max.copy()
n_inliers = temp_n
H = np.linalg.lstsq(matched2[max_inliers], matched1[max_inliers])[0]
H[:, 2] = np.array([0, 0, 1])
### END YOUR CODE
print(H)
return H, matches[max_inliers]
def hog_descriptor(patch, pixels_per_cell=(8,8)):
"""
按照如下步骤生成HOG描述符:
1. 计算x- 以及 y-方向的梯度图像 (已经算好了)
2. 对于每个cell,计算梯度直方图
3. 对于每个block,将它们平铺成一维的向量。
在此, 我们将整个patch都视作一个block
4. 将平铺后的block进行标准正态化
正态化会使得描述子对于光照变化更加robust
参数:
patch: 尺寸为 (H, W) 的灰度图
pixels_per_cell: 每个cell的尺寸 (M, N)
提示:
你可能会用到view_as_blocks函数
Returns:
block: 一维向量,表征该patch的特征描述向量,尺寸为: ((H*W*n_bins)/(M*N))
"""
assert (patch.shape[0] % pixels_per_cell[0] == 0),\
'Heights of patch and cell do not match'
assert (patch.shape[1] % pixels_per_cell[1] == 0),\
'Widths of patch and cell do not match'
n_bins = 9
degrees_per_bin = 180 // n_bins
Gx = filters.sobel_v(patch)
Gy = filters.sobel_h(patch)
# 无符号梯度
G = np.sqrt(Gx**2 + Gy**2)
theta = (np.arctan2(Gy, Gx) * 180 / np.pi) % 180
# 将尺寸为(M, N)的cell视作一个像素点
# G_cells.shape = theta_cells.shape = (H//M, W//N)
# G_cells[0, 0].shape = theta_cells[0, 0].shape = (M, N)
G_cells = view_as_blocks(G, block_shape=pixels_per_cell)
theta_cells = view_as_blocks(theta, block_shape=pixels_per_cell)
rows = G_cells.shape[0]
cols = G_cells.shape[1]
# 对于每个cell, 计算梯度直方图。它的尺寸是n_bins
cells = np.zeros((rows, cols, n_bins))
# 对于每个cell,计算梯度直方图
### YOUR CODE HERE
# Compute histogram per cell
for i in range(rows):
for j in range(cols):
for m in range(pixels_per_cell[0]):
for n in range(pixels_per_cell[1]):
idx = int(theta_cells[i, j, m, n] // degrees_per_bin)
if idx == 9:
idx = 8
cells[i, j, idx] += G_cells[i, j, m, n]
cells = (cells - np.mean(cells)) / np.std(cells)
block = cells.reshape(-1)
### YOUR CODE HERE
return block
def linear_blend(img1_warped, img2_warped):
"""
按照下列步骤,将图片 img1_warped 和图片 img2_warped 进行线性混合:
1. 确定 left 和 right 空白位置 (已经帮你完成)
2. 为img1_warped 和 img2_warped分别确定一个权重矩阵
你可能会用到np.linspace 和 np.tile 函数
3. 将权重矩阵分别应用到它们对应的图片里
4. 将图像合并到一起
Args:
img1_warped: 输出图像里img1的部分
img2_warped: 输出图像里img2的部分
Returns:
merged: 融合到一起的图像
"""
out_H, out_W = img1_warped.shape # 输出图像的尺寸
img1_mask = (img1_warped != 0) # Mask == 1 inside the image
img2_mask = (img2_warped != 0) # Mask == 1 inside the image
# 找出img1在输出图像里面最右边的column
# 这是我们img1权重矩阵的终点(也就是权重值为0所对应的位置)
right_margin = out_W - np.argmax(np.fliplr(img1_mask)[out_H//2, :].reshape(1, out_W), 1)[0]
# 找出img2在输出图像里面最左边的column
# 这是我们img2权重矩阵的起点(也就是权重值为1所对应的位置)
left_margin = np.argmax(img2_mask[out_H//2, :].reshape(1, out_W), 1)[0]
### YOUR CODE HERE
left_matrix = np.array(img1_mask, dtype=np.float64)
right_matrix = np.array(img2_mask, dtype=np.float64)
left_matrix[:, left_margin: right_margin] = np.tile(np.linspace(1, 0, right_margin - left_margin), (out_H, 1))
right_matrix[:, left_margin: right_margin] = np.tile(np.linspace(0, 1, right_margin - left_margin), (out_H, 1))
img1 = left_matrix * img1_warped
img2 = right_matrix * img2_warped
merged = img1 + img2
### END YOUR CODE
return merged
def stitch_multiple_images(imgs, desc_func=simple_descriptor, patch_size=5):
"""
将一系列图片拼接到一起.
参数:
imgs: 长度为m的List,每个元素都是图片,并且图片是有序排列的。
desc_func: 特征描述函数,输入一张图,输出为它所对应的描述算子
patch_size: 每个特征点所对应的局部图像的尺寸。为了简化,这里将长宽设定成相同。
Returns:
panorama: 最终生成的全景图
"""
# 对于每张照片,检测其特征点
keypoints = [] # keypoints[i] 对应于 imgs[i]
for img in imgs:
kypnts = corner_peaks(harris_corners(img, window_size=3),
threshold_rel=0.05,
exclude_border=8)
keypoints.append(kypnts)
# 描述特征点
descriptors = [] # descriptors[i] 对应于 keypoints[i]
for i, kypnts in enumerate(keypoints):
desc = describe_keypoints(imgs[i], kypnts,
desc_func=desc_func,
patch_size=patch_size)
descriptors.append(desc)
# 将相邻图片的特征点匹配到一起
matches = [] # matches[i] 记录了 descriptors[i] 与 descriptors[i+1]的match点
H = []
robust_matches = []
for i in range(len(imgs)-1):
mtchs = match_descriptors(descriptors[i], descriptors[i+1], 0.7)
matches.append(mtchs)
h, robust_m = ransac(keypoints[i], keypoints[i+1], matches[i])
H.append(h)
robust_matches.append(robust_m)
#利用match的像素点完成图像的拼接
### YOUR CODE HERE
output_shape, offset = get_output_space(imgs[1], [imgs[0], imgs[2], imgs[3]],
[np.linalg.inv(H[0]), H[1], np.dot(H[1],H[2])])
img1_warped = warp_image(imgs[0], np.linalg.inv(H[0]), output_shape, offset)
img1_mask = (img1_warped != -1)
img1_warped[~img1_mask] = 0
img2_warped = warp_image(imgs[1], np.eye(3), output_shape, offset)
img2_mask = (img2_warped != -1)
img2_warped[~img2_mask] = 0
img3_warped = warp_image(imgs[2], H[1], output_shape, offset)
img3_mask = (img3_warped != -1)
img3_warped[~img3_mask] = 0
img4_warped = warp_image(imgs[3], np.dot(H[1], H[2]), output_shape, offset)
img4_mask = (img4_warped != -1)
img4_warped[~img4_mask] = 0
panorama = linear_blend(img1_warped, img2_warped)
panorama = linear_blend(panorama, img3_warped)
panorama = linear_blend(panorama, img4_warped)
### END YOUR CODE
return panorama
# Python 3.6
# utils.py
import numpy as np
from scipy.ndimage import affine_transform
# 完成欧式坐标与齐次坐标之间的转换
pad = lambda x: np.hstack([x, np.ones((x.shape[0], 1))])
unpad = lambda x: x[:,:-1]
def plot_matches(ax, image1, image2, keypoints1, keypoints2, matches,
keypoints_color='k', matches_color=None, only_matches=False):
"""将匹配的特征点给绘制出来.
参数
----------
ax : matplotlib.axes.Axes
坐标轴,用于绘制图像以及匹配点对.
image1 : (N, M [, 3]) array
灰度图或者彩色图像.
image2 : (N, M [, 3]) array
灰度图或者彩色图像.
keypoints1 : (K1, 2) array
图1的关键点 ``(row, col)``.
keypoints2 : (K2, 2) array
图2的关键点 ``(row, col)``.
matches : (Q, 2) array
match点对的序号。
每一行第一个值是keypoints1的序号,第二个值是keypoints2的序号
keypoints_color : matplotlib color, optional
指定绘制的颜色,可选.
matches_color : matplotlib color, optional
两点连线的颜色.
only_matches : bool, optional
是否绘制keypoint点的坐标.
"""
image1.astype(np.float32)
image2.astype(np.float32)
new_shape1 = list(image1.shape)
new_shape2 = list(image2.shape)
if image1.shape[0] < image2.shape[0]:
new_shape1[0] = image2.shape[0]
elif image1.shape[0] > image2.shape[0]:
new_shape2[0] = image1.shape[0]
if image1.shape[1] < image2.shape[1]:
new_shape1[1] = image2.shape[1]
elif image1.shape[1] > image2.shape[1]:
new_shape2[1] = image1.shape[1]
if new_shape1 != image1.shape:
new_image1 = np.zeros(new_shape1, dtype=image1.dtype)
new_image1[:image1.shape[0], :image1.shape[1]] = image1
image1 = new_image1
if new_shape2 != image2.shape:
new_image2 = np.zeros(new_shape2, dtype=image2.dtype)
new_image2[:image2.shape[0], :image2.shape[1]] = image2
image2 = new_image2
image = np.concatenate([image1, image2], axis=1)
offset = image1.shape
if not only_matches:
ax.scatter(keypoints1[:, 1], keypoints1[:, 0],
facecolors='none', edgecolors=keypoints_color)
ax.scatter(keypoints2[:, 1] + offset[1], keypoints2[:, 0],
facecolors='none', edgecolors=keypoints_color)
ax.imshow(image, interpolation='nearest', cmap='gray')
ax.axis((0, 2 * offset[1], offset[0], 0))
for i in range(matches.shape[0]):
idx1 = matches[i, 0]
idx2 = matches[i, 1]
if matches_color is None:
color = np.random.rand(3)
else:
color = matches_color
ax.plot((keypoints1[idx1, 1], keypoints2[idx2, 1] + offset[1]),
(keypoints1[idx1, 0], keypoints2[idx2, 0]),
'-', color=color)
def get_output_space(img_ref, imgs, transforms):
"""
Args:
img_ref: 参考图(reference image)
imgs: 需要被变换的图片(images to be transformed)
transforms: affine变换矩阵所组成的一个List. transforms[i] 将图片 imgs[i]中的点 map 到 img_ref
Returns:
输出image的尺寸
"""
assert (len(imgs) == len(transforms))
r, c = img_ref.shape
corners = np.array([[0, 0], [r, 0], [0, c], [r, c]])
all_corners = [corners]
for i in range(len(imgs)):
r, c = imgs[i].shape
H = transforms[i]
corners = np.array([[0, 0], [r, 0], [0, c], [r, c]])
warped_corners = corners@H[:2,:2] + H[2,:2]
all_corners.append(warped_corners)
# 找出Corner的边界
all_corners = np.vstack(all_corners)
# 整幅输出图的形状是两个最远的conrner相减
corner_min = np.min(all_corners, axis=0)
corner_max = np.max(all_corners, axis=0)
output_shape = (corner_max - corner_min)
# 确保输出是整数
output_shape = np.ceil(output_shape).astype(int)
offset = corner_min
return output_shape, offset
def warp_image(img, H, output_shape, offset):
# 需要注意 affine_transfomr 这个函数:
# 给定一个输出图像的像素点 o,
# 它的像素值是由下式所决定的:
# np.dot(matrix,o) + offset.
# 因此, 我们需要将转换矩阵求一个逆.
# 这样反向求的好处是,插值更加方便。
Hinv = np.linalg.inv(H)
m = Hinv.T[:2,:2]
b = Hinv.T[:2,2]
img_warped = affine_transform(img.astype(np.float32),
m, b+offset,
output_shape,
cval=-1)
return img_warped
7 实施例
7.1 Harris角点部分
我们首先从Harris角点检测开始
# 初始化配置
import numpy as np
from skimage import filters
from skimage.feature import corner_peaks
from skimage.io import imread
import matplotlib.pyplot as plt
from time import time
from panorama import harris_corners
%matplotlib inline
plt.rcParams['figure.figsize'] = (15.0, 12.0) # 设置默认尺寸
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 自动重装外部模块
%load_ext autoreload
%autoreload 2
img = imread('sudoku.png', as_gray=True)
# 计算Harris角点响应值
response = harris_corners(img)
# 显示角点响应值
plt.imshow(response)
plt.axis('off')
plt.title('Harris Corner Response')

# 对Harris响应图片进行非极大值抑制
# 然后输出响应点的坐标
corners = corner_peaks(response, threshold_rel=0.01)
# 显示角点
plt.imshow(img)
plt.scatter(corners[:,1], corners[:,0], marker='x')
plt.axis('off')
plt.title('Detected Corners')
plt.show()
from panorama import harris_corners
img1 = imread('uttower1.jpg', as_grey=True)
img2 = imread('uttower2.jpg', as_grey=True)
# 利用Harris角点检测算法检测两张图片中的关键点
keypoints1 = corner_peaks(harris_corners(img1, window_size=3),
threshold_rel=0.05,
exclude_border=8)
keypoints2 = corner_peaks(harris_corners(img2, window_size=3),
threshold_rel=0.05,
exclude_border=8)
# 显示检测到的关键点
plt.subplot(1,2,1)
plt.imshow(img1)
plt.scatter(keypoints1[:,1], keypoints1[:,0], marker='x')
plt.axis('off')
plt.title('Detected Keypoints for Image 1')
plt.subplot(1,2,2)
plt.imshow(img2)
plt.scatter(keypoints2[:,1], keypoints2[:,0], marker='x')
plt.axis('off')
plt.title('Detected Keypoints for Image 2')
plt.show()

由此,得到了角点特征,我们需要进行匹配描述。找到两组描述子集合中相匹配的向量。首先,从两张图片中各取一个描述子(也就是关键点生成的向量),计算它们的欧氏距离。利用欧氏距离来判定它们是 不是对应的一组描述子:如果这一对描述子的距离显著小于其他的距离,那么我们认为它们是一组对应的特征点。该函数的输出会是一组数列(array),数列的每一行都是一组对应的 描述子索引号(index)。
from panorama import simple_descriptor, match_descriptors, describe_keypoints
from utils import plot_matches
patch_size = 5
# 利用关键点生成描述向量(描述子)
desc1 = describe_keypoints(img1, keypoints1,
desc_func=simple_descriptor,
patch_size=patch_size)
desc2 = describe_keypoints(img2, keypoints2,
desc_func=simple_descriptor,
patch_size=patch_size)
# 将描述子进行匹配
matches = match_descriptors(desc1, desc2, 0.7)
# 画出匹配的点
fig, ax = plt.subplots(1, 1, figsize=(15, 12))
ax.axis('off')
plot_matches(ax, img1, img2, keypoints1, keypoints2, matches)
plt.show()

现在,我们已经有一组描述子的对应列表。我们将利用这组对应列表计算从图片二映射到图片一的变换矩阵。换句话说,如果图片1中的点 与图片2中的点
相匹配, 我们需要找出一个仿射变换矩阵来进行坐标变换,使得
其中,和
都是齐次坐标。
需要注意的是,矩阵很有可能不能使得每一组对应点都完全匹配,但是我们可以利用最小二乘法来进行估计最优的矩阵H。假设给定了
组匹配的特征点,让
和
为两个
的矩阵,矩阵的每一行都是对应特征点的齐次坐标(也就是原坐标后面补1)。那么,我们知道矩阵
应该满足条件:
from panorama import fit_affine_matrix
# 检查变换矩阵求解是否正确
# 测试值
a = np.array([[0.5, 0.1], [0.4, 0.2], [0.8, 0.2]])
b = np.array([[0.3, -0.2], [-0.4, -0.9], [0.1, 0.1]])
H = fit_affine_matrix(b, a)
# 期望的输出值
sol = np.array(
[[1.25, 2.5, 0.0],
[-5.75, -4.5, 0.0],
[0.25, -1.0, 1.0]]
)
error = np.sum((H - sol) ** 2)
if error < 1e-20:
print('Implementation correct!')
else:
print('There is something wrong.')
from utils import get_output_space, warp_image
# 获取特征点
p1 = keypoints1[matches[:,0]]
p2 = keypoints2[matches[:,1]]
# 求解变换矩阵
H = fit_affine_matrix(p1, p2)
output_shape, offset = get_output_space(img1, [img2], [H])
print("Output shape:", output_shape)
print("Offset:", offset)
# 进行坐标变换
img1_warped = warp_image(img1, np.eye(3), output_shape, offset)# 图片1没变,因此用单位阵作为变换矩阵
img1_mask = (img1_warped != -1) # Mask不等于-1表示该位置为原图片插值后的点
img1_warped[~img1_mask] = 0 # Mask取反表示在该位置没有值(该位置为背景),置0使得该位置变黑
img2_warped = warp_image(img2, H, output_shape, offset)
img2_mask = (img2_warped != -1) # Mask不等于-1表示该位置为原图片插值后的点
img2_warped[~img2_mask] = 0 # Mask取反表示在该位置没有值(该位置为背景),置0使得该位置变黑
# 画出坐标变换后的图像
plt.subplot(1,2,1)
plt.imshow(img1_warped)
plt.title('Image 1 warped')
plt.axis('off')
plt.subplot(1,2,2)
plt.imshow(img2_warped)
plt.title('Image 2 warped')
plt.axis('off')
plt.show()
运行输出结果:Output shape: [496 615]
Offset: [-39.37184617 0. ]

merged = img1_warped + img2_warped
# 确定哪些值被加了两次
overlap = (img1_mask * 1.0 + # bool 型转成 float
img2_mask)
# 重合部分的值除以2,未重合的部分除以1,以保证亮度一致
normalized = merged / np.maximum(overlap, 1)
plt.imshow(normalized)
plt.axis('off')
plt.show()

好了,这就是最终的拼接结果。不知道你心中是否有很多问号,甚至想发出“就这就这就这就这就这”的疑惑。我们来分析一下产生这个结果的原因,在特征点匹配的时候,我们发现特征进行了非常不错的对应,并且可视化了出来,因此问题并不是出在特征检测这一步。
而在这之后,为了使图像进行变形,我们采用了求解仿射变换矩阵的方式进行仿射变换,在这一步,我们的结果出现了问题,这是因为在确定对应点时,我们的限制条件并不算精确,导致引入了许多无效数据。我们可以利用 RANSAC ("Random Sample Consensus",随机抽样一致)方法来进一步对数据进行筛选,求解变换矩阵。
RANSAC的主要步骤包括了:
- 随机选取对应点
- 计算变换矩阵
- 在给定的阈值范围内计算有效数据点数(inliers)
- 重复步骤1-3,记录下最多的有效点数
- 利用有效的数据点和最小二乘法重新计算变换矩阵
from panorama import ransac
# 设置相同的seed以保证生成的随机数相同
np.random.seed(131)
H, robust_matches = ransac(keypoints1, keypoints2, matches, threshold=1)
# 显示利用RANSAC的结果
fig, ax = plt.subplots(1, 1, figsize=(15, 12))
plot_matches(ax, img1, img2, keypoints1, keypoints2, robust_matches)
plt.axis('off')
plt.show()

现在,我们可以利用新计算的到的转换矩阵来生成一张更稳定的全景图像了。
output_shape, offset = get_output_space(img1, [img2], [H])
# 进行坐标变换
img1_warped = warp_image(img1, np.eye(3), output_shape, offset)# 图片1不变,因此用单位阵作为变换矩阵
img1_mask = (img1_warped != -1) # Mask不等于-1表示该位置为原图片插值后的点
img1_warped[~img1_mask] = 0 # Mask取反表示在该位置没有值(该位置为背景),置0使得该位置变黑
img2_warped = warp_image(img2, H, output_shape, offset)
img2_mask = (img2_warped != -1) # Mask不等于-1表示该位置为原图片插值后的点
img2_warped[~img2_mask] = 0 # Mask取反表示在该位置没有值(该位置为背景),置0使得该位置变黑
# 显示坐标变换后的图片
plt.subplot(1,2,1)
plt.imshow(img1_warped)
plt.title('Image 1 warped')
plt.axis('off')
plt.subplot(1,2,2)
plt.imshow(img2_warped)
plt.title('Image 2 warped')
plt.axis('off')
plt.show()
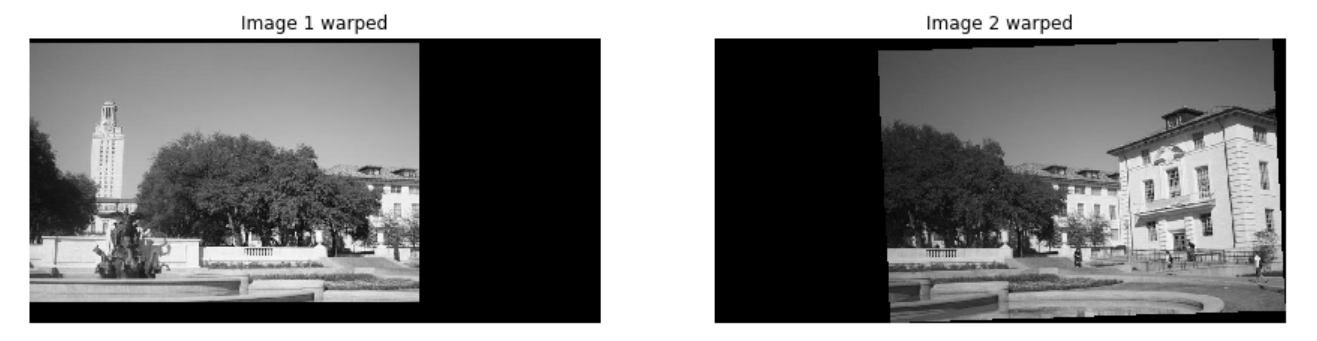
merged = img1_warped + img2_warped
# 确定哪些值被加了两次
overlap = (img1_mask * 1.0 + # bool 型转成 float
img2_mask)
# 重合部分的值除以2,未重合的部分除以1,以保证亮度一致
normalized = merged / np.maximum(overlap, 1)
plt.imshow(normalized)
plt.axis('off')
plt.show()

7.2 梯度方向直方图部分
在前面的计算中, 我们利用simple_descriptor来计算特征点的特征向量。但在这一模块里,我们将会利用HOG来计算特征点的特征。
HOG 值得是梯度方向直方图。在HOG算法中,我们利用梯度的方向分布来当做特征向量。梯度(x和y方向)在一幅图片中是很有用的,我们可以利用它的大小来判断点的类型,例如边缘等。
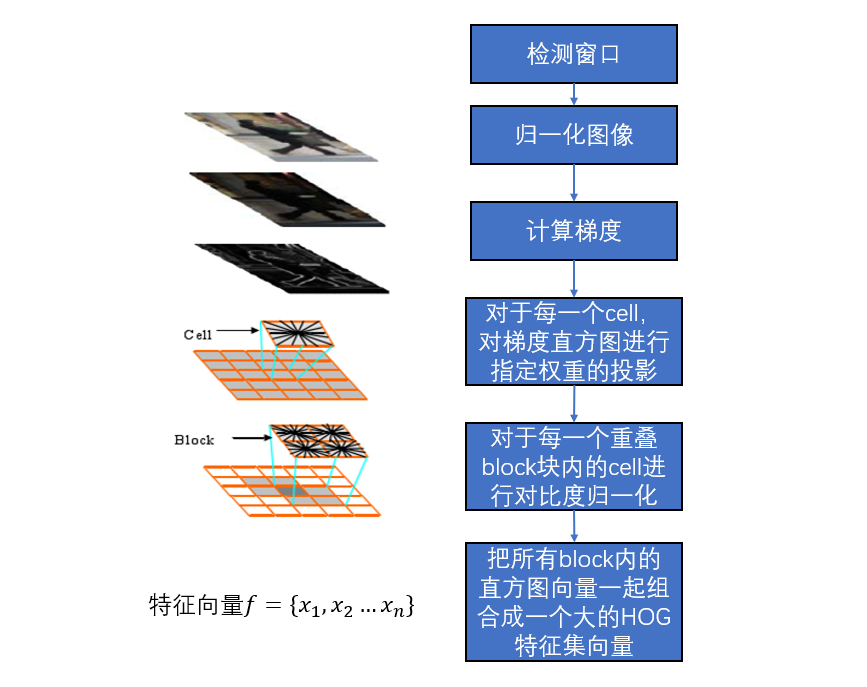
HOG的步骤包括:
- 计算x和y方向的梯度图像
- 计算梯度直方图:将图片分成若干个cell,并对每个cell计算梯度直方图
- 将若干个cell合成一个block,并将里面的梯度直方图转成特征向量
- 将特征向量归一化
from panorama import hog_descriptor
img1 = imread('uttower1.jpg', as_grey=True)
img2 = imread('uttower2.jpg', as_grey=True)
# 关键点检测
keypoints1 = corner_peaks(harris_corners(img1, window_size=3),
threshold_rel=0.05,
exclude_border=8)
keypoints2 = corner_peaks(harris_corners(img2, window_size=3),
threshold_rel=0.05,
exclude_border=8)
# 提取特征
desc1 = describe_keypoints(img1, keypoints1,
desc_func=hog_descriptor,
patch_size=16)
desc2 = describe_keypoints(img2, keypoints2,
desc_func=hog_descriptor,
patch_size=16)
# 特征匹配
matches = match_descriptors(desc1, desc2, 0.7)
# 画出匹配的特征
fig, ax = plt.subplots(1, 1, figsize=(15, 12))
ax.axis('off')
plot_matches(ax, img1, img2, keypoints1, keypoints2, matches)
plt.show()

from panorama import ransac
# 设置相同的seed以保证生成的随机数相同
np.random.seed(131)
H, robust_matches = ransac(keypoints1, keypoints2, matches, threshold=1)
# 画出匹配的点
fig, ax = plt.subplots(1, 1, figsize=(15, 12))
plot_matches(ax, img1, img2, keypoints1, keypoints2, robust_matches)
plt.axis('off')
plt.show()
plt.imshow(imread('solution_hog_ransac.png'))
plt.axis('off')
plt.title('HOG descriptor + RANSAC Solution')
plt.show()

output_shape, offset = get_output_space(img1, [img2], [H])
# 坐标变换
img1_warped = warp_image(img1, np.eye(3), output_shape, offset)# 图片1只需要平移,因此用单位阵作为变换矩阵
img1_mask = (img1_warped != -1) # Mask不等于-1表示该位置为原图片插值后的点
img1_warped[~img1_mask] = 0 # Mask取反表示在该位置没有值(该位置为背景),置0使得该位置变黑
img2_warped = warp_image(img2, H, output_shape, offset)
img2_mask = (img2_warped != -1) # Mask不等于-1表示该位置为原图片插值后的点
img2_warped[~img2_mask] = 0 # Mask取反表示在该位置没有值(该位置为背景),置0使得该位置变黑
# 画出坐标变换后的图像
plt.subplot(1,2,1)
plt.imshow(img1_warped)
plt.title('Image 1 warped')
plt.axis('off')
plt.subplot(1,2,2)
plt.imshow(img2_warped)
plt.title('Image 2 warped')
plt.axis('off')
plt.show()
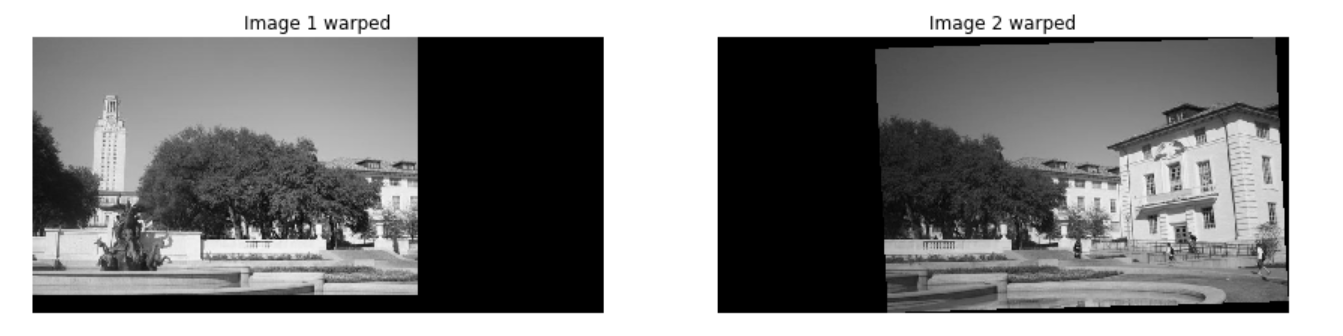
merged = img1_warped + img2_warped
# 确定哪些值被加了两次
overlap = (img1_mask * 1.0 + # bool 型转成 float
img2_mask)
# 重合部分的值除以2,未重合的部分除以1,以保证亮度一致
normalized = merged / np.maximum(overlap, 1)
plt.imshow(normalized)
plt.axis('off')
plt.show()
plt.imshow(imread('solution_hog_panorama.png'))
plt.axis('off')
plt.title('HOG Descriptor Panorama Solution')
plt.show()

7.3 简单的图片融合策略
可以发现,在最终的输出图片里,融合区域存在明显的分界线。这些分界线并不是我们想要的,因此需要把它们去掉,其中有一个非常简单的方法叫做线性融合(linear blending)。
在前面计算融合图片的时候,我们将重合区域的强度值除以了2,其他部分除以1。这其实表示的是左右两张图片的比重相同(equally weighted)。但实际上,重合区域左右两边的比重并不应该相同:靠近左边图片的部分,左边图片的比重应该更大;靠近右边图片的部分,右边图片的比重 应该更大。据此,我们可以利用线性融合的方法来提升最终全景图片的质量。
线性融合可以用以下几步进行实现:
- 确定融合区域的左边界和右边界;
- 给图片1确定一个权重矩阵:
- 从图片1的最左边到融合区域的最左边,weight为1;
- 从融合区域的最左边到图片1的最右边,weight从1到0进行分布;
- 给图片2确定一个权重矩阵:
- 从融合区域的最右边到图片2的最右边,weight为1;
- 从融合区域的最左边到图片1的最右边,weight从0到1进行分布;
- 分别对左右两张图片应用权重矩阵;
- 将两张图相加。
from panorama import linear_blend
img1 = imread('uttower1.jpg', as_grey=True)
img2 = imread('uttower2.jpg', as_grey=True)
# 设置相同的seed以保证生成的随机数相同
np.random.seed(131)
# 检测特征点
keypoints1 = corner_peaks(harris_corners(img1, window_size=3),
threshold_rel=0.05,
exclude_border=8)
keypoints2 = corner_peaks(harris_corners(img2, window_size=3),
threshold_rel=0.05,
exclude_border=8)
# 提取特征描述向量
desc1 = describe_keypoints(img1, keypoints1,
desc_func=hog_descriptor,
patch_size=16)
desc2 = describe_keypoints(img2, keypoints2,
desc_func=hog_descriptor,
patch_size=16)
# 进行特征描述向量的匹配
matches = match_descriptors(desc1, desc2, 0.7)
H, robust_matches = ransac(keypoints1, keypoints2, matches, threshold=1)
output_shape, offset = get_output_space(img1, [img2], [H])
# 将图片放到最终输出图里面
img1_warped = warp_image(img1, np.eye(3), output_shape, offset)
img1_mask = (img1_warped != -1) # Mask == 1 inside the image
img1_warped[~img1_mask] = 0 # Return background values to 0
img2_warped = warp_image(img2, H, output_shape, offset)
img2_mask = (img2_warped != -1) # Mask == 1 inside the image
img2_warped[~img2_mask] = 0 # Return background values to 0
# 将两张图片拼成一张
merged = linear_blend(img1_warped, img2_warped)
plt.imshow(merged)
plt.axis('off')
plt.show()

7.4 多图像的配准——全景图像拼接
假设现在你有张图片
,我们可以把相邻的两张图片当成一组,然后计算图片
到图片
的坐标转换矩阵,也就是前面我们所完成的affine变换矩阵。接着,我们可以选择最中间的一张照片作为参考图片(reference image
),并将其他照片的坐标系统转换到该图片中来,从而完成
张图片的拼接。
from panorama import stitch_multiple_images
# 设置相同的seed以保证生成的随机数相同
np.random.seed(131)
# 载入需要进行拼接的图片
img1 = imread('yosemite1.jpg', as_grey=True)
img2 = imread('yosemite2.jpg', as_grey=True)
img3 = imread('yosemite3.jpg', as_grey=True)
img4 = imread('yosemite4.jpg', as_grey=True)
imgs = [img1, img2, img3, img4]
# 将图片拼接到一起
panorama = stitch_multiple_images(imgs, desc_func=simple_descriptor, patch_size=5)
# 显示拼接后的图片
plt.imshow(panorama)
plt.axis('off')
plt.show()

7.5 拓展讨论
本文的代码为了减少计算量,是对灰度图像进行处理的,但这并不意味着不能对彩色图像进行特征提取与拼接。计算特征并基于特征配准,这对于彩色图像而言其实同样可行,基于灰度图像的特征或综合三通道的图像进行特征匹配,都可以并实现彩色图像上的拼接。
此外,在了解图像拼接领域的相关研究中,有3到4种主流的图像拼接方向,其中非常有意思的一种是基于网格变形的图像拼接(Shape-Preserving Half-Projective(SPHP),2014CVPR),其方法是求解一个最优的公共平面将所有图像映射到公共平面上。
SPHP从形状矫正的角度出发,非重叠区域逐渐过渡到全局相似,并对整个图像增加相似变换约束,矫正拼接图像的形状,减少投影失真(算法的核心思想——网格变形,如下图)

算法流程图如下:
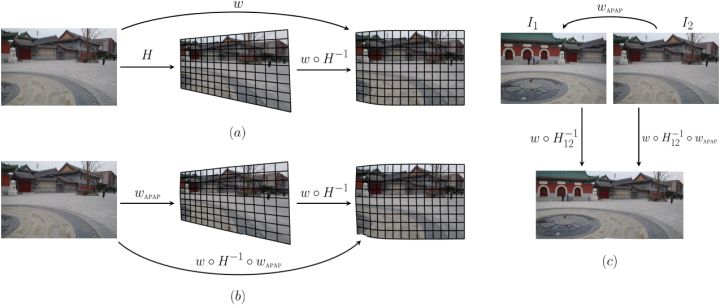
其Matlab代码可以在该网址下载:www.cmlab.csie.ntu.edu.tw/~frank/SPH/cvpr14_SPHP_code.tar
该方法的特征点匹配结果:


该方法的拼接结果有非常好的效果,可以做到对图像局部非线性畸变的矫正,这是网格变形的优势所在。


有兴趣的朋友可以自行了解该领域的相关方法,特征与配准目前仍是计算机视觉领域的热点研究方向。
8 写在最后
Harris角点检测的参考文献,1988发表,被引用次数17316
[1] Harris C G, Stephens M. A combined corner and edge detector[C]//Alvey vision conference. 1988, 15(50): 10-5244.
谷歌学术和百度学术都没法看这篇88年的文章的原文,估计有点老了....放个某国内文档网的在线浏览页面吧 max.book118.com/html/2017/0…
方向梯度直方图的参考文献,IJCV和CVPR都是计算机视觉三大顶会之一,[2]2005年发表,被引用次数30607,[3]2012年发表,被引166
[2] Dalal N , Triggs B . Histograms of Oriented Gradients for Human Detection[C]// 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). IEEE, 2005.
[3] Chandrasekhar V , Takacs G , Chen D M , et al. Compressed Histogram of Gradients: A Low-Bitrate Descriptor[J]. International Journal of Computer Vision, 2012, 96(3):384-399.
SPHP图像拼接,2014年发表,被引量158:
[4] Chang C H, Sato Y, Chuang Y Y. Shape-preserving half-projective warps for image stitching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2014: 3254-3261.