1.概述
随着信息的暴增,人们所面临的一个挑战就是如何从提供的大量商品或信息中快速简单地找到他们最需要的东西。为了解决这一问题而提出来的“推荐系统”应运而生。最开始推荐系统只是简单的协同过滤策略,但是随着系统的发展,演化出来召回-排序-重排复杂的结构。召回处在这个系统的前置位,决定了排序的天花板。本文讲了最常见的协同过滤方法。 协同过滤基于“集体智慧”的思想,该方法认为,人们倾向某种人群共性的部分。例如,你想看一部电影,但不知道看哪部,大部分人都会问问周围的人,并倾向与选择平时与自己爱好口味比较类似的人的推荐。协同过滤优点在于,该方法对领域不敏感,即不需要对推荐事务很了解也可以,同时效果往往也比基于内容的方法好。但协同过滤会产生“冷启动”困难的问题。 下文主要讲常用的几种协同过滤算法。
2. 算法
2.1 邻域CF
2.1 原理
基于邻域的协同过滤算法是推荐最常见的算法之一。优点是:实现成本低,不容易出错,计算速度快,效果不错,能推荐长尾的物品。缺点是尾部点击少的user和item容易出现badcase。 最近邻方法”包括“基于物品的协同过滤”和“基于用户的协同过滤”。“基于物品的协同过滤”-Item based 是指寻找与物品a相似的其他物品,当用户观看了物品a 时, 给用户推荐相似的其他物品。“基于用户的协同过滤”-User based 是指寻找与用户A相似的其他用户B,C,D, 如果用户A和用户B观看喜好相似,由于用户A和用户B很相似,那么认为用户B看过的其他物品b也很有可能被A所喜欢。以Koren的图为例说明user-based方法, Joe喜欢左边的三部电影a,b,c,为Joe推荐电影时,找到与他相似的用户A,B,C,这三个人都看过电影1,拯救大兵瑞恩,因此,这部电影是最先推荐的。
2.2 计算方法
以item-base的方法举例,说明如何计算item-item的相似度。 假设user A观看或点击了item a,b(以下统称点击),同样,user B点击了item b, item d,user C点击了item a, item b , item c。
| item a | item b | item c | item d | |
|---|---|---|---|---|
| user A | 1 | 1 | ||
| user B | 1 | 1 | ||
| user C | 1 | 1 | 1 |
将该点击序列展开,得到矩阵

2.3 结论
- 会存在一些“非用户点击”,即机器爬虫等,特点是点击量过高,需要去掉。
- 在物品中,尽管我们希望每个物品都至少推给用户一次,对长尾有很好的作用,但是在某些情况下,对于点击特别少的,默认质量不高,也可以去掉。
- 在计算时,不要真正展开成向量,而是分别计算item a 出现的次数,item b出现的次数,以及itam a 和itam b共同出现的次数,就可以了。因此该方法很适合并行。
- 基于物品和用户的协同过滤根据不同场景来选择。比如,在亚马逊购物网站,用户的数量远远高于物品的数量,且用户的喜好变换很大,在不同的时期购买的东西不相同,相似性不稳定,而物品数量相对用户较小,且物品与物品之间的相似性较稳定,因此更常用item-based。
2.OCF(order-cf)
2.1 原理
Item-CF是拿到全量信息后,计算item与item的相似度,对所有点击的item同等对待,没有考虑到点击的顺序。OCF则考虑了点击序列的前后顺序。例如,在新闻场景中,点击了文章A之后点击的文章B相对于文章A之前点击的文章C,文章B与文章A更相关。
2.2 计算方法
| 符号 | 意义 |
|---|---|
| i,j | item |
| order(i,j) | 在某一个transaction中,j在i之后点击记为1,否则记为0 |
| click(i) | i被点击的总次数 |
| N | transaction的总次数 |
2.3 ocf的改进
上面的方法默认了在文章A后点击的全部都是同等重要的。但是往往用户的兴趣会随着时间漂移,如在点击浏览文章a之后,立刻点击的文章b比点了10篇文章后再点击的文章c可能会更相似。因为随着文章的增多,用户的兴趣可能被不断转移。基于以上假设,因此提出基于位置假说的oicf,公式如下:
其实就是给每个位置赋予不同的权重,越靠近原文章的点击权重越大。
3. SCF
3.1 原理
该方法来自阿里的文章《基于图结构的实时推荐算法SWING的工程实现》。 假设如下图所示
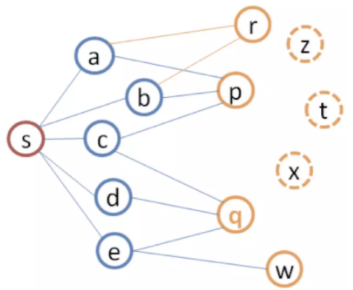
3.2 计算
| 符号 | 意义 |
|---|---|
| i,j | item |
| u,v | user |
| 参数 | |
| 点击过i的user集合 | |
| 点击过j的user集合 |
SCF更多的利用了user的collective intelligence
3.3 结论
由公式可以看到,如果同时点击i,j的人越多,越大。低俗的文章很多用户去点,就很容易排到前面,因此SCF很容易出热门、低俗。可以通过其他手段来控制和解决。
一个user点击的item,一天最多也就是几百左右,在计算的时候,问题不大。但是一个item会被上百万甚至上千万用户点击,这些用户会做一个两两pair去计算,因此会产生大量的时间消耗。这里需要一些优化。优化的关键是组合(u1, u2)。
- 广播Map(item, userList)和Map(user, itemList);
- 将RDD(u1, i1)->RDD(u1, itemList) -> RDD((i1, i2), u) -> RDD((i1, i2), (u1, u2)) -> 计算每一对(i1, i2) score -> 按照key(i1, i2)加和
- 另外一个改进是可以只计算(userA, userB),因为score(A,B)=score(B,A) ,所有保存的时候写入(userA, userB, score)和(userB, userA, score)
4. FM 矩阵分解
不同于前面的简单计算,矩阵分解属于模型方法,需要优化求解。
4.1 原理 矩阵变换
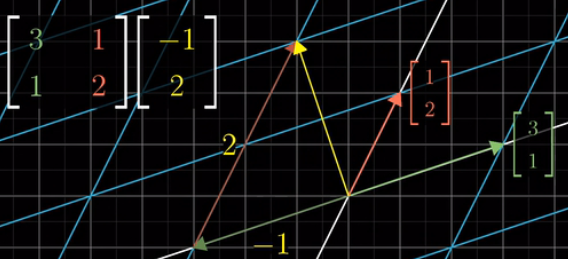
矩阵变换的本质是一个函数,与普通函数不同的是矩阵变换接收一个向量,并输出一个向量。也就是一个向量运动变成另外一个向量,原来的单位向量移动到了新的位置。举例存在一个向量
变换前
变换后
假设
,
,
得到
也就是如果得到变换后
和
的位置,也就是确定了新的坐标参考系,就可以得到该空间任意向量
的位置。把这两个向量写到一起,就是矩阵乘法
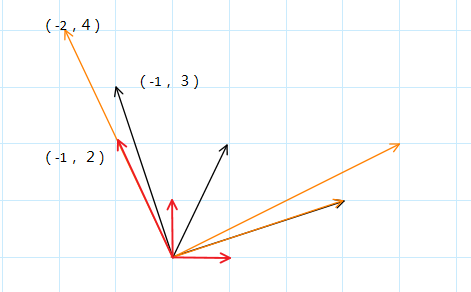
用图表示就是:
4.2 基础模型
基础的矩阵分解模型为,其中
为用户u对item i的评分,
为item的向量,
为用户u 的向量。优化目标为:
为已知
的(u,i)集合。
因为q 和 p都不知道,因此该等式不是凸函数,其求解方法为ALS(Alternating least squares).每次固定其中的一个,比如p,然后这个最优化问题等价于二次优化问题,用SGD求关于p最优解,然后再固定p,求关于q的最优化问题,如此迭代。
4.3 考虑偏差
由于每个用户的消费习惯不同,有用户偏向给每个电影的评分更高,有的用户偏低,因此在基础模型上,叠加了偏差。
优化目标为:
为全部item的平均值。举例来说,预测Joe对Titanic的评分,所有电影的平均得分是3.7,Titanic是一部好电影,比普通电影得分高0.7,Joe是一个谨慎的用户,评分比其他用户要低0.3左右,因此最终的得分为3.9(3.7+0.5-0.3)。
4.4 隐式反馈场景
上述矩阵分解最常用的场景是显示反馈,而我们现在需要做的是隐式反馈。显示反馈是指用户明确的知道自己的态度,例如给电影评分等。隐式反馈并不能直接反应用户的态度,例如点击数据、浏览数据,用户的一次点击并不以为这用户喜欢这个物品或者喜欢这篇新闻。隐式反馈和显示反馈很不相同,隐式反馈更稠密,更稳定;而显示反馈更稀疏。 隐式反馈更真实,数据更容易获得;显示反馈更能说明用户的态度。隐式数据的处理方法不同于显示数据。当前对于这两类数据有两种方法: point wise(预测对点的偏好) 和pair wise(对两个item的排序)。对隐式数据而言,优化方法变成了(与原文保持一致,p,q 分别改成了x,y):