

————— 第二天 —————



什么意思呢?让我们来举一个例子:
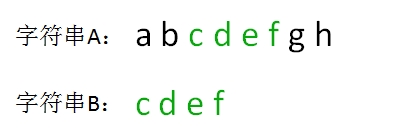
在上图中,字符串B是A的子串,B第一次在A中出现的位置下标是2(字符串的首位下标是0),所以返回 2。
我们再看另一个例子:
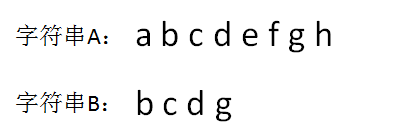
在上图中,字符串B在A中并不存在,所以返回 -1。
为了统一概念,在后文中,我们把字符串A称为主串,把字符串B称为模式串。


小灰的想法简单粗暴,让我们用下面的例子来演示一下:
第一轮,我们从主串的首位开始,把主串和模式串的字符逐个比较:
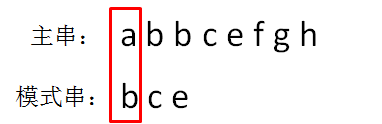
显然,主串的首位字符是a,模式串的首位字符是b,两者并不匹配。
第二轮,我们把模式串后移一位,从主串的第二位开始,把主串和模式串的字符逐个比较:
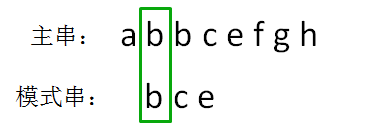
主串的第二位字符是b,模式串的第二位字符也是b,两者匹配,继续比较:
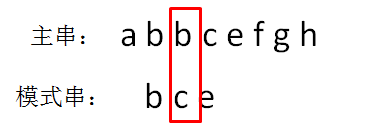
主串的第三位字符是b,模式串的第三位字符也是c,两者并不匹配。
第三轮,我们把模式串再次后移一位,从主串的第三位开始,把主串和模式串的字符逐个比较:
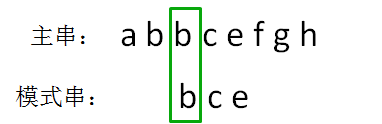
主串的第三位字符是b,模式串的第三位字符也是b,两者匹配,继续比较:
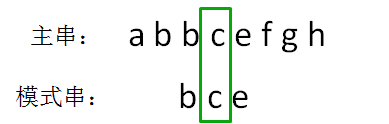
主串的第四位字符是c,模式串的第四位字符也是c,两者匹配,继续比较:
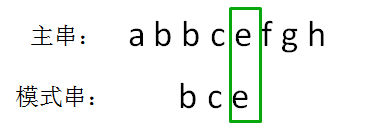
主串的第五位字符是e,模式串的第五位字符也是e,两者匹配,比较完成!
由此得到结果,模式串 bce 是主串 abbcefgh 的子串,在主串第一次出现的位置下标是 2:
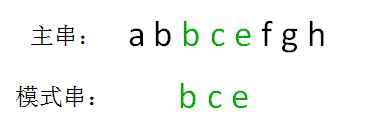
以上就是小灰想出的解决方案,这个算法有一个名字,叫做BF算法,是Brute Force(暴力算法)的缩写。



上图的情况,在每一轮进行字符匹配时,模式串的前三个字符a都和主串中的字符相匹配,一直检查到模式串最后一个字符b,才发现不匹配:

这样一来,两个字符串在每一轮都需要白白比较4次,显然非常浪费。
假设主串的长度是m,模式串的长度是n,那么在这种极端情况下,BF算法的最坏时间复杂度是O(mn)。




————————————







比较哈希值是什么意思呢?
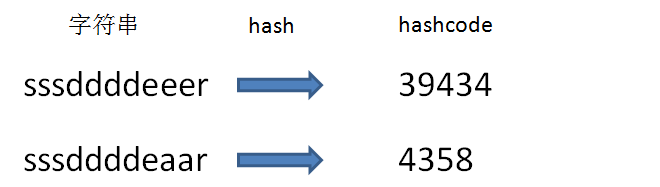
用过哈希表的朋友们都知道,每一个字符串都可以通过某种哈希算法,转换成一个整型数,这个整型数就是hashcode:
hashcode = hash(string)
显然,相对于逐个字符比较两个字符串,仅比较两个字符串的hashcode要容易得多。

给定主串和模式串如下(假定字符串只包含26个小写字母):

第一步,我们需要生成模式串的hashcode。
生成hashcode的算法多种多样,比如:
按位相加
这是最简单的方法,我们可以把a当做1,b当做2,c当做3......然后把字符串的所有字符相加,相加结果就是它的hashcode。
bce = 2 + 3 + 5 = 10
但是,这个算法虽然简单,却很可能产生hash冲突,比如bce、bec、cbe的hashcode是一样的。
转换成26进制数
既然字符串只包含26个小写字母,那么我们可以把每一个字符串当成一个26进制数来计算。
bce = 2*(26^2) + 3*26 + 5 = 1435
这样做的好处是大幅减少了hash冲突,缺点是计算量较大,而且有可能出现超出整型范围的情况,需要对计算结果进行取模。
为了方便演示,后续我们采用的是按位相加的hash算法,所以bce的hashcode是10:
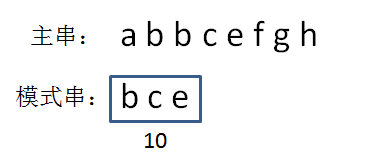
第二步,生成主串当中第一个等长子串的hashcode。
由于主串通常要长于模式串,把整个主串转化成hashcode是没有意义的,只有比较主串当中和模式串等长的子串才有意义。
因此,我们首先生成主串中第一个和模式串等长的子串hashcode,
即abb = 1 + 2 + 2 = 5:
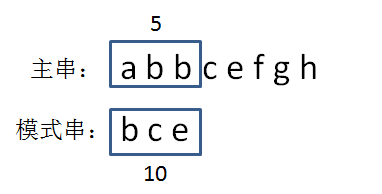
第三步,比较两个hashcode。
显然,5!=10,说明模式串和第一个子串不匹配,我们继续下一轮比较。
第四步,生成主串当中第二个等长子串的hashcode。
bbc = 2 + 2 + 3 = 7:

第五步,比较两个hashcode。
显然,7!=10,说明模式串和第二个子串不匹配,我们继续下一轮比较。
第六步,生成主串当中第三个等长子串的hashcode。
bce= 2 + 3 + 5 = 10:
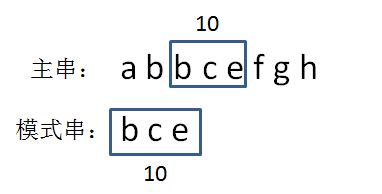
第七步,比较两个hashcode。
显然,10 ==10,两个hash值相等!这是否说明两个字符串也相等呢?
别高兴的太早,由于存在hash冲突的可能,我们还需要进一步验证。
第八步,逐个字符比较两字符串。
hashcode的比较只是初步验证,之后我们还需要像BF算法那样,对两个字符串逐个字符比较,最终判断出两个字符串匹配。
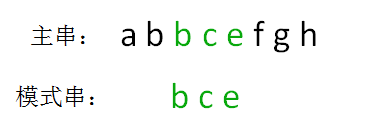
最后得出结论,模式串bce是主串abbcefgh的子串,第一次出现的下标是2。


什么意思呢?让我们再来看一个例子:

上图中,我已知子串abbcefg的hashcode是26,那么如何计算下一个子串,也就是bbcefgd的hashcode呢?
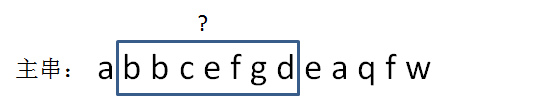
我们没有必要把子串的字符重新进行累加运算,而是可以采用一个更简单的方法。由于新子串的前面少了一个a,后面多了一个d,所以:
新hashcode = 旧hashcode - 1 + 4 = 26-1+4 = 29
再下一个子串bcefgde的计算也是同理:
新hashcode = 旧hashcode - 2 + 5 = 29-2+5 = 32


public static int rabinKarp(String str, String pattern){ //主串长度 int m = str.length(); //模式串的长度 int n = pattern.length(); //计算模式串的hash值 int patternCode = hash(pattern); //计算主串当中第一个和模式串等长的子串hash值 int strCode = hash(str.substring(0, n)); //用模式串的hash值和主串的局部hash值比较。 //如果匹配,则进行精确比较;如果不匹配,计算主串中相邻子串的hash值。 for (int i=0; i<m-n+1; i++) { if(strCode == patternCode && compareString(i, str, pattern)){ return i; } //如果不是最后一轮,更新主串从i到i+n的hash值 if(i<m-n){ strCode = nextHash(str, strCode, i, n); } } return -1;}private static int hash(String str){ int hashcode = 0; //这里采用最简单的hashcode计算方式: //把a当做1,把b当中2,把c当中3.....然后按位相加 for (int i = 0; i < str.length(); i++) { hashcode += str.charAt(i)-'a'; } return hashcode;}private static int nextHash(String str, int hash, int index, int n){ hash -= str.charAt(index)-'a'; hash += str.charAt(index+n)-'a'; return hash;}private static boolean compareString(int i, String str, String pattern) { String strSub = str.substring(i, i+pattern.length()); return strSub.equals(pattern);}public static void main(String[] args) { String str = "aacdesadsdfer"; String pattern = "adsd"; System.out.println("第一次出现的位置:" + rabinKarp(str, pattern));}






—————END—————
喜欢本文的朋友,欢迎关注公众号 程序员小灰,收看更多精彩内容
