计算视觉——先验之于图像手绘/素描风格转换的妙用常见的经验状态一般可分为两种：先验和后验。后验一般需要体验过才能知道，

先验与后验

常见的经验状态一般可分为两种：先验和后验。

后验一般需要体验过才能知道，比如一门课程第一年考试，这门考试的难度如何。又或者这杯新品奶茶它好不好喝。

而先验则是藉由经验或逻辑论证所形成建立起来的，比如沸腾的水是滚烫的，所以看到沸腾的水我们不会直接去喝/触摸。对应后验的例子来解释先验，如果我们有某一门课程近几年的试卷，那我们大致就了解了这门考试的难度。

而先验和后验都并不一定代表完全正确的经验状态，也就是说虽然有先验（或后验）等作为支撑依据，但仍然有可能得出错误的结果或结论，这一点需要明确，两者都有各自的弊端，这不会在本文中重点讨论，有兴趣的朋友可以自行了解。

图像风格转换(Image Style Transfer)需求的诞生

不同的图像都存在一种“风格”，对于绘画作品而言，指的是一种”画风“，对于拍摄所得的照片而言，也有其自己的照片风格。而随着移动拍摄设备（手机）的增多，产生了越来越多的拍摄图像处理上的需求，比如常见的滤镜、美颜、贴图，本质上都是在图像上进行了计算处理。

近年来，随着多种多样的视频软件、拍摄软件出现在大众的视线中，也产生了各种各样的需求，图像风格转换是其中非常有趣的一者。

比如下图(c)具有(a)的轮廓，相应位置的内容几乎是一样的。但是整幅图像的属性（比如颜色，纹理）都变成了(b)的。阿凡达画风的蒙娜丽莎，原本为绘制的熊猫(a)转换成了真实风格的熊猫(c)。这一系列图像风格（包括纹理和色域色调）发生变化但维持基本形状轮廓不变的的图像处理，被称为图像风格转换。

当然，我们也可以反向实现这个过程，即以上图(b)作为待转换图像，(a)作为风格参考图像，实现的结果也非常有趣，如下图所示。

实现图像风格转换的方法非常之多，现在主流方向主要还是基于深度学习神经网络框架的，比如对抗生成网络GAN就有不少在图像风格转换的应用。就本质而言，深度学习中所用到的数据集和参数训练这一过程也是对先验的应用，但是这不够典型，也不够巧妙。

本文要介绍的图像处理算法是一种固定风格的转换，是一种不基于深度学习的传统算法。

图像转换为手绘风格中面临的问题及分析

对于手绘风格的图像风格转换，相信有读者已经在相关的拍摄软件中用过，手绘风格是一种图像转换中较常见的风格。

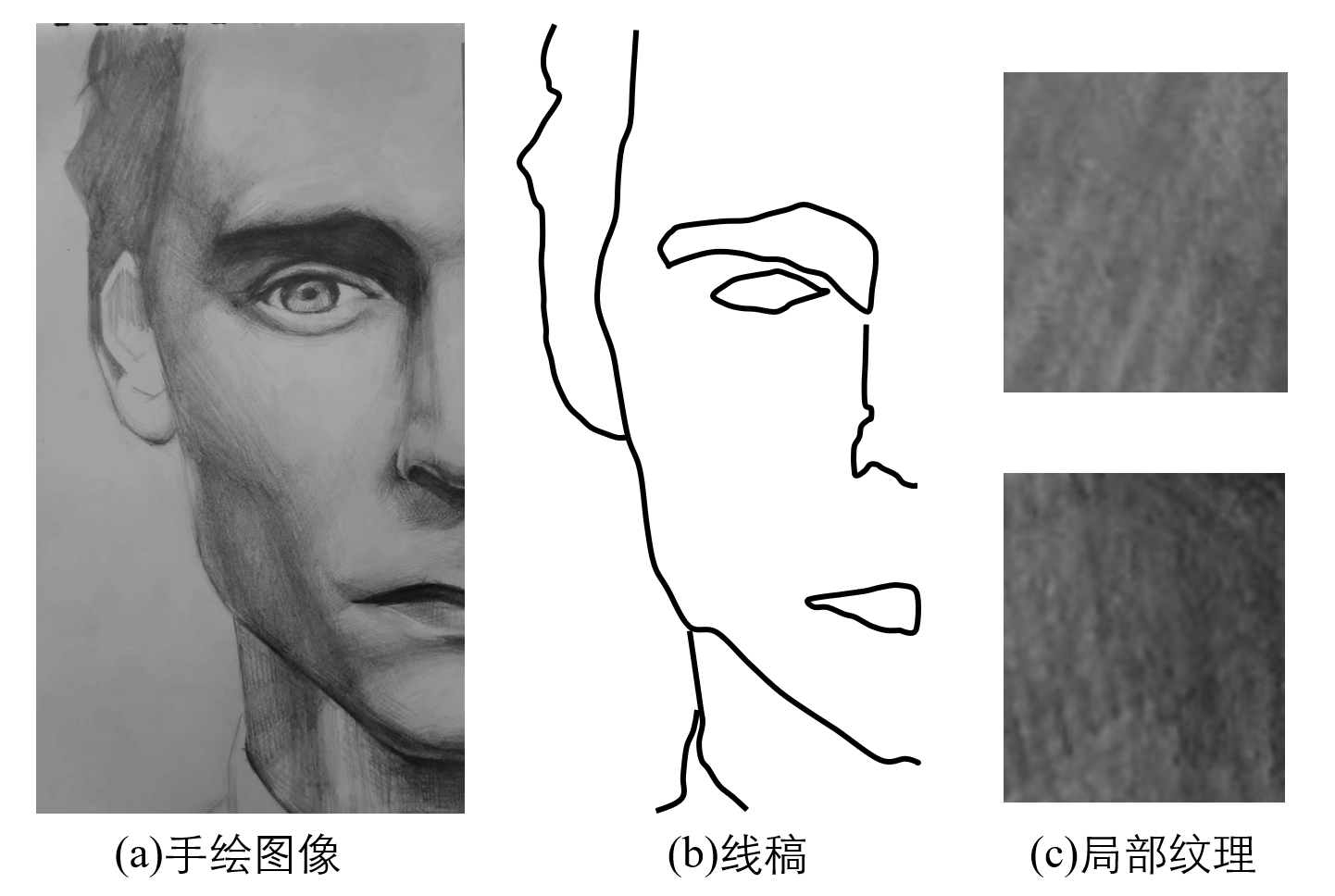
但是看似简单的效果背后，却面临很多麻烦的问题。为了更好的说明问题，我从近期本专业同学的朋友圈找了一张手绘图像（因为博主刚好是计算机+艺术设计复合型专业的学生）。

通过观察我们不难发现，我们可以发现线稿与tone局部纹理是手绘稿中的显著特征。一副手绘图像可以简单的分为纹理与线稿，分别对应于视觉认知中的颜色（纹理）与形状（线稿），如下图所示。

(a)是一幅实际的手绘素描稿，而(b)是潦草的线稿((b)是我画的，有点搞笑，假冒伪劣产品既视感)...大家能通过图片明白什么是线稿就可以了。

因此，如何实现图像手绘风格转换的问题可以得到更为具体的转化，即如何将图像的颜色转化为手绘风格中的纹理并且将图像的边缘转化为手绘风格中的线稿。在这里，（我们用到了一种问题转化的思想，把一个笼统的抽象的问题（怎么转化风格）通过实际的问题分析，转化成了更具象化的问题（如何实现A到B，C到D的转换），即通过转化问题并解决被转化后的问题来解决原问题，这是一种非常常见的研究方法和解决问题的方法）。

线稿

艺术家们在进行手绘时，往往会将一条曲线画成多条短、频繁的线段，因此这些线条不仅会有交合线，而且手绘图像中的曲线看似是一条曲弧，实际上该曲线是由多条短而断裂的线条频繁的绘制在一起的结果，如下图所示。

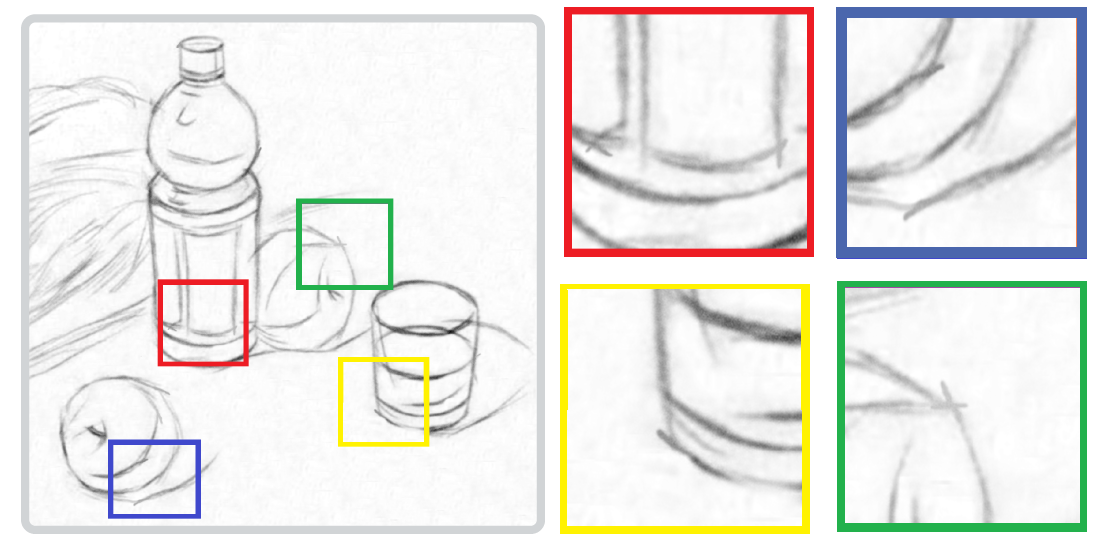
从而引出的第一个问题是，如何提取绘画风格中的线条，一个容易想到的解决方法就是利用图像的梯度信息，以图像的边缘作为手绘风格的线条，这自然是行之有效的，但也存在问题。

对于线稿如何生成这一问题，原文作者对此的描述为：在素描中，线条（stroke）的属性包括：线宽（thickness）、起伏（wiggliness）、明暗（brightness）；线条通常结束于弯曲点（points of curvature）或交叉点（junctions）且几乎没有连续长曲线。

但是，如果直接以图像梯度信息作为线条线稿，我们显然不可能得到手绘的交合线条与断裂线条。第一个问题更进一步的细化为，是否有方法可以将图像的梯度信息转化为手绘线稿风格的线条。

答案自然是有的，方法其实和Canny算子中的非极大值抑制（Non-Maximum Suppression）有着非常相近的实现手段，能够理解canny算子中的非极大值抑制就很容易理解后续操作。

首先，提取一幅图像的梯度信息，如下式所述

G=\sqrt{(\partial _xI)^2+(\partial _yI)^2}

其中， $I$ 为灰度图像， $\partial _x\partial _y$ 分别为图像在两个方向上的梯度。通过上式获得的图像梯度图信息，所提取的通常是有噪的且不包含用于线条生成的连续边缘。

第二步，线条方向估计，这一过程与非极大值抑制的相似性非常高。选择间隔为45°的8个参考方向，记为线段 $\{ \varphi_i\},i\in\{1...8\}$ ，某个方向的响应图为

其中， $\varphi_i$ 为第 $i$ 上方向的线段，并表示成卷积核形式；线段长度取值为输入图像长（宽）的1/30; $*$ 符号表示卷积算子，计算梯度在各方向上投影，构造滤波器响应图 $G_i$ .

第三步，分类。按梯度在所有方向上投影的最大值对梯度分类，需要注意的是，论文原文（见Eq.(3)，链接放在了本文最后）的数学表述为

C_i=\begin{cases} G(p),if \ \mathop{\arg\min}_i G_i=i\\0,\ \ \ \ \ \ otherwise\end{cases}

实际上，因为需要的是投影的最大值，上式的 $\min$ 应该改为 $\max$ ，这应该是作者的疏忽，正确的表述如下：

C_i=\begin{cases} G(p),if \ \mathop{\arg\max}_i G_i=i\\0,\ \ \ \ \ \ otherwise\end{cases}

其中， $p$ 为像素索引； $C_i$ 是 $i$ 方向上的幅度图，如下图（即为幅度图），且满足 $\sum_{i=1}^8 C_i = G$ 。通过分类这一步可以有较好的抗噪声能力和一定程度的鲁棒性。

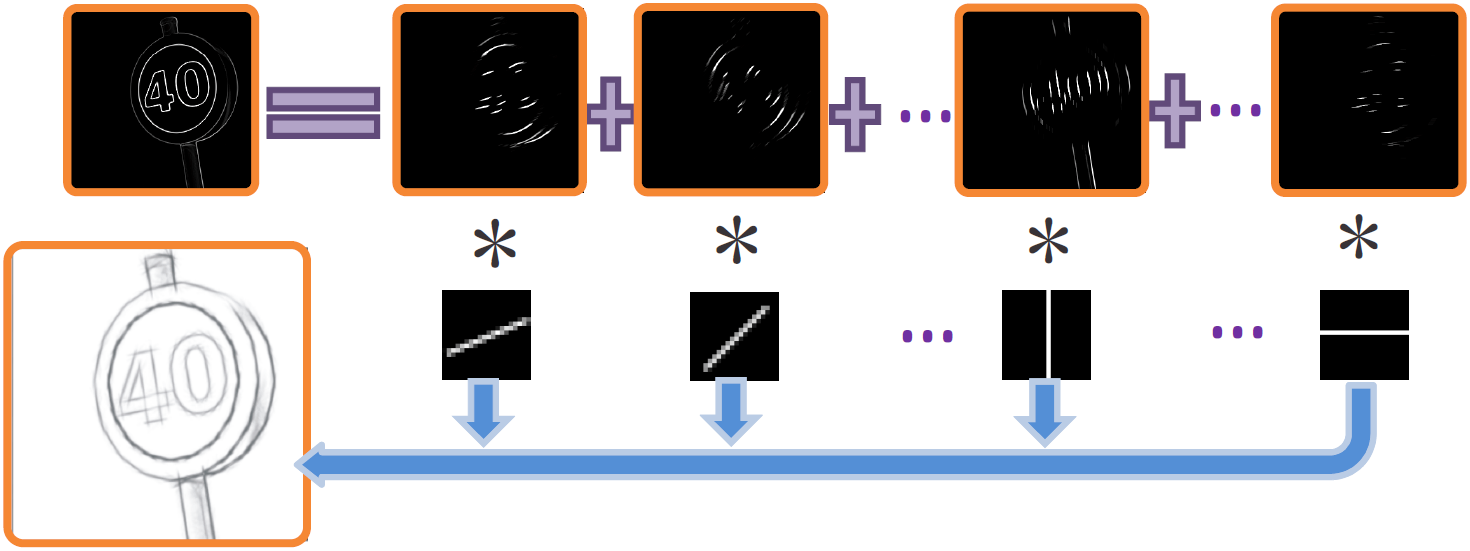
线稿生成中的最后一步，线条生成，表示为：

沿给定方向进行卷积平滑，能够连接原始梯度图中不相连的边缘像素。 $S′$ 经逆向处理并归一化至[0,1]后得到输出线条图 $S$ 。

我们可以比较一下通过这种方法得到的线稿的结果(见下图(c))。

一方面，有非常明显的交合线与断裂线，看起来更有手绘的风格，完全可以以假乱真。

另一方面，在第二步和第三步非常像非极大值抑制的流程中，对于图像纹理的噪声有很好的抑制效果，如下图(c)。

色调转移与局部纹理绘制

在图像转换为手绘风格中面临的问题及分析这一节中，我们分析了手绘风格转换中的问题。线条的问题已在上述的处理中得到了解决，那么另一个问题，手绘风格的纹理该如何再现呢？在这个问题的解决中，我们终于用到了题目中的先验。 ~~不说我都快忘记了...我这篇文章是拿来讲先验的妙用的~~

首先先解释一下何为手绘和素描中的tone(色调)，作者用以下文字进行描述：影线，即稠密线条，用于表现阴影和较暗物体。

实际上，也就是这种铅笔涂出来的纹理。

接下来，我们将用到图像先验。

通过统计自然图像和手绘图像的直方图，可以得到如下图所示的统计规律。自然场景的图像像素直方图如(c)所示，而手绘素描则如(d)所示。

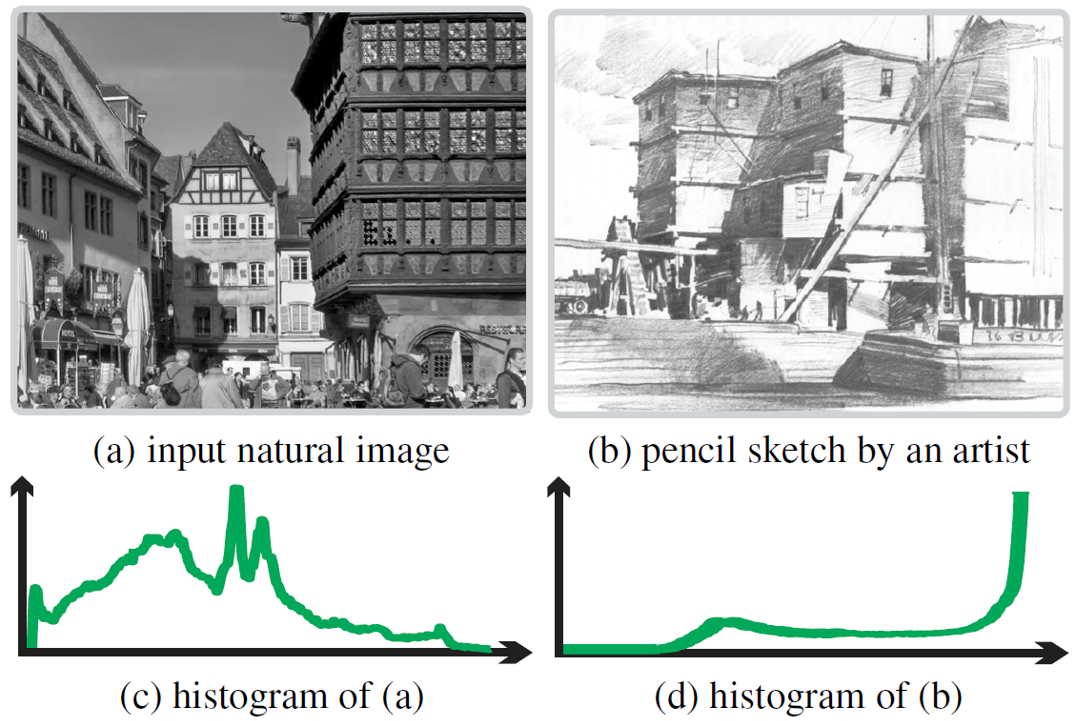
对于现实图像，直方图通常不存在显著规律，而手绘素描图像的直方图就看起来存在着一定的规律。

作者用以下的文字描述：自然图像的色调通常变化明显如(c)的直方图，而素描色调直方图服从特定的模式（certain patterns），如(d)的直方图。这是因为素描有两种基本色调：（1）高光区域；（2）阴影区域。在两种基本色调之间是过渡区域，用于丰富画面层次感。

基于此，作者提出了一种色调分布的参数模型，通过模型实现色调转移。

基于模型的色调转移(model-based tone transfer)

假设：所有手绘素描都基本符合如(d)所示的直方图分布模式。
基本的想法：将一幅给定图像的直方图强制转化映射至(d)型的直方图
基于三段函数拟合模型
- 在图像表现上，明暗层次明确，与手绘素描相符，可以满足风格转换的需求
- 由函数曲线拟合的模型，像素值的过渡平滑
- 思想易懂，也能产生很好的结果

拟合色调分布参数模型的数学表述如下：

其中， $v$ 表示色调值(tone value)； $p(v)$ 表示像素色调取值为 $v$ 的概率； $Z$ 为使 $\int^{1}_{0}{p(v)dv}=1$ 的归一化因子；权值 $w_i$ 与各层像素数量有关。此外，色调值需要进行归一化处理，保证其动态范围在 $[0,1]$ 中。

而如下图所示，(a)为一幅手绘素描，(b)为作者根据像素的值把(a)分成三层分别以绿、橘、蓝色标出（绿为最暗的一部分区域，橘）。根据作者的观察，给出了三层的色调分布。

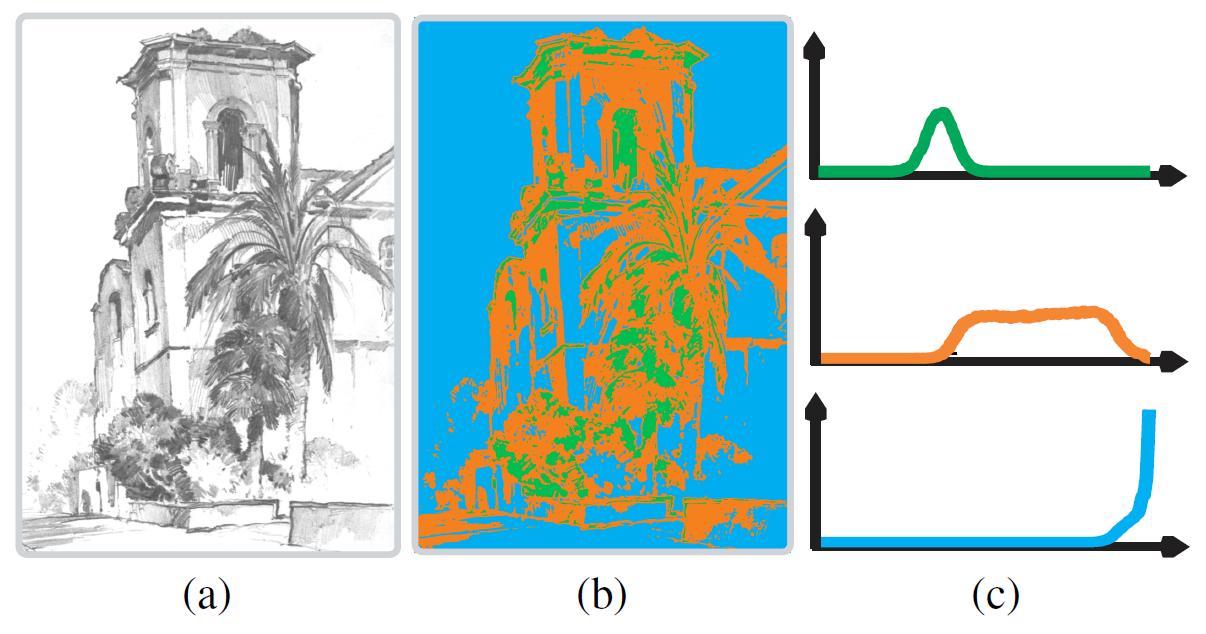
此处是猜测，作者应该尝试过2层、4层分布的模型，但3层的效果是最易于解释也是较好的

不知道大家发现了没有，上图的(c)其实就是先前对一幅手绘素描图像直方图统计先验结果的拆分，如下图。

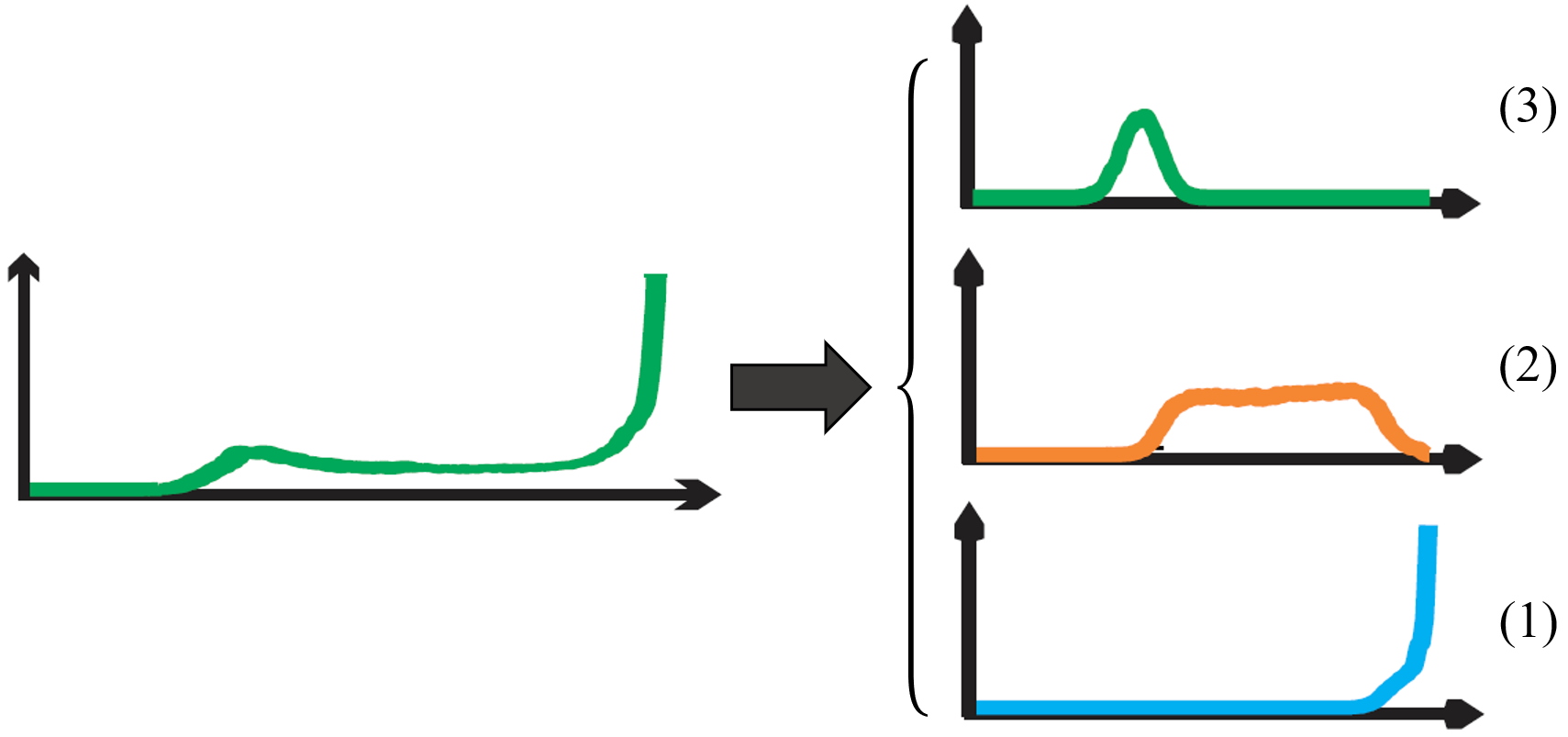
具体来说，暗层(3)和亮层(1)有明显的峰值，而由于炭笔上石墨与白纸接触的性质，明暗中间层(2)并不对应于一个独特的峰值。

现在大家来观察一下(1)(2)(3)的曲线形状，如果让你来用你见过最像的函数拟合这三条曲线，你会如何选择。

对于(2)(3)而言，答案呼之欲出。(3)曲线可以用高斯函数（也就是正态分布）拟合，(2)曲线如果忽略两端的起伏，基本在一条水平的线上，可以用均匀分布相应的函数拟合。

那么，唯一的问题就是(1)曲线的拟合该用什么函数了。如果是数学、物理、统计或者通信相关专业的同学可能知道答案：用拉普拉斯分布的一半进行拟合，即单边拉普拉斯分布响应函数。

给出三种曲线的拟合模型式：

1.首先是描述阴影区域的高斯函数模型

p_1(v)=\begin{cases} \frac{1}{\sigma_b}e^{-\frac{1-v}{\sigma_b}},\ if \ \
v\le1\\0,\ \ \ \ \ \ \ \ \ \ \ \ \ otherwise\end{cases}

其中， $\sigma_b$ 为拉普拉斯分布函数的尺度参数， $v$ 为像素值。

2.介于高光与阴影中间的纹理区域对应的均匀分布模型

p_2(v)=\begin{cases} \frac{1}{u_b-u_a},\ \ if \ \
u_a\le v\le u_b\\\ 0,\ \ \ \ \ \ \ \ \ otherwise\end{cases}

其中，， $u_a$ $u_b$ 分别为均匀分布分布范围的上下界。

3.描述高光区域的单边拉普拉斯模型

p_3(v)=\frac{1}{\sqrt{2\pi}\sigma_d}e^{-\frac{(v-\mu_d)^2}{2\sigma^2_d}}

而上面这个公式是修改后的，原文的公式Eq.(7)有误，原文错误公式如下：

其中， $\mu_d$ 为(3)阴影区域的像素均值， $\sigma_d$ 为尺度参数。

参数学习(Parameter Learning)

有了三段具体的函数模型后，需要做的是分别对其进行参数估计，实现该模型对手绘图像的直方图先验曲线拟合。具体实施步骤如下：

对输入灰度图 $I$ 轻微的高斯平滑。设定各层的色调阈值，权值 $w$ 取决于各层中的像素数量；使用极大似然估计计算各层参数。各层的均值和标准差分别记为 $\bar{m}$ 、 $\bar{s}$ ，则各层参数的解析解分别为：

\sigma_b = \frac{1}{N}\sum^N_{i=1} |x_i-1|

u_a=m_m-\sqrt 3 s_m , u_b=m_m+\sqrt 3 s_m

其中， $x_i$ 为像素值；N为该层所含像素个数； $x_i\in[0,1]$ 。

极大似然估计过程

极大似然估计过程如下：

(1) $p_1(v),x_i\in X, X=\{x_1,...,x_N \}$ 表示高光层所有像素的集合

\sigma_b^* =\mathop{\arg\min}_{\sigma_b}p(X,\sigma_b) \\\ \ \ \ \ \ \ \ \ \ =\mathop{\arg\min}_{\sigma_b}\prod^N_{i=1}p(x_i,\sigma_b)\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\mathop{\arg\min}_{\sigma_b}\sum^N_{i=1}\log p(x_i,\sigma_b) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\mathop{\arg\min}_{\sigma_b}\sum^N_{i=1}(-\log \sigma_b-\frac{1-x_i}{\sigma_b}))

令 $\frac{\partial p}{\partial \sigma_b}=0$ ，则

\sum^N_{i=1}(-\frac{1}{\sigma_b}+\frac{1-x_i}{\sigma_b^2})=0

由此可得

\sigma_b^*=\frac{1}{N}\sum^N_{i=1}(1-x_i)

(2) $p_2(v),x_i\in X, X=\{x_1,...,x_N \}$ 表示中间层所有像素的集合，对 $\mu_a \mu_b$ 进行区间估计

(3) $p_3(v),x_i\in X, X=\{x_1,...,x_N \}$ 表示阴影层所有像素的集合

通过极大似然估计，作者给出了三组不同的参数以及对应的效果，但其效果相差不大，如下图所示。

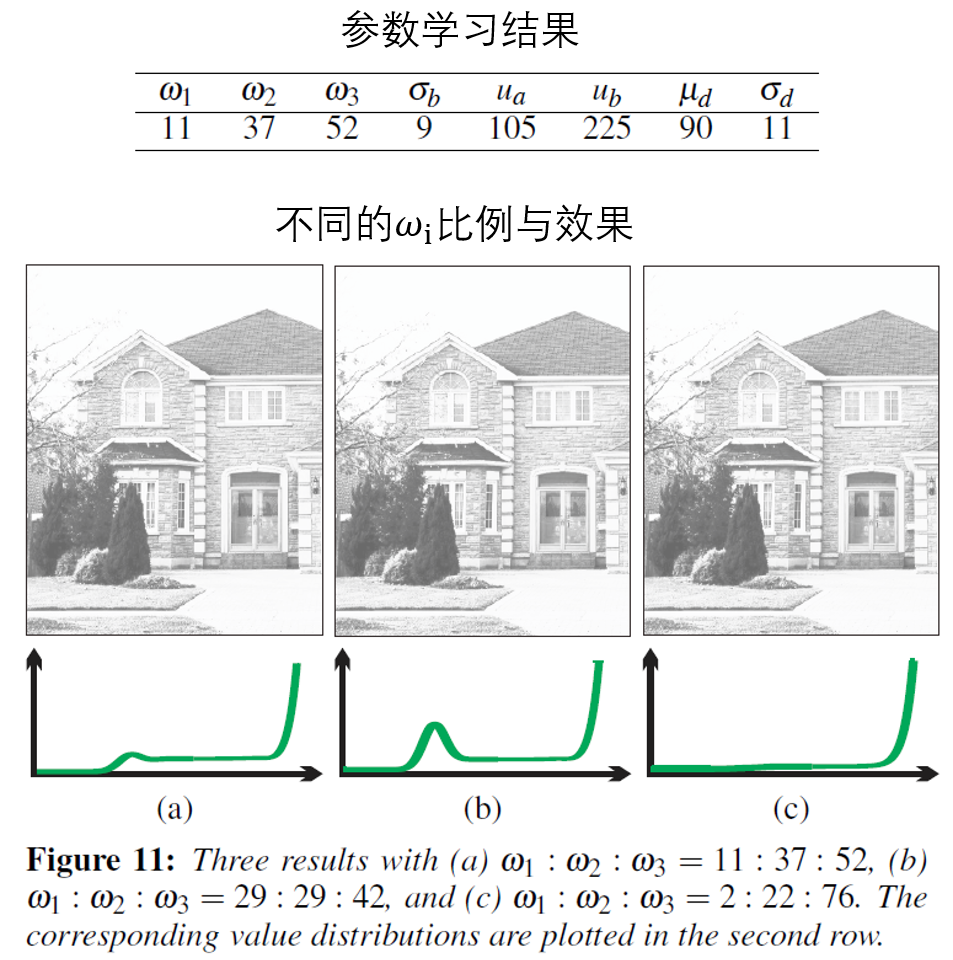
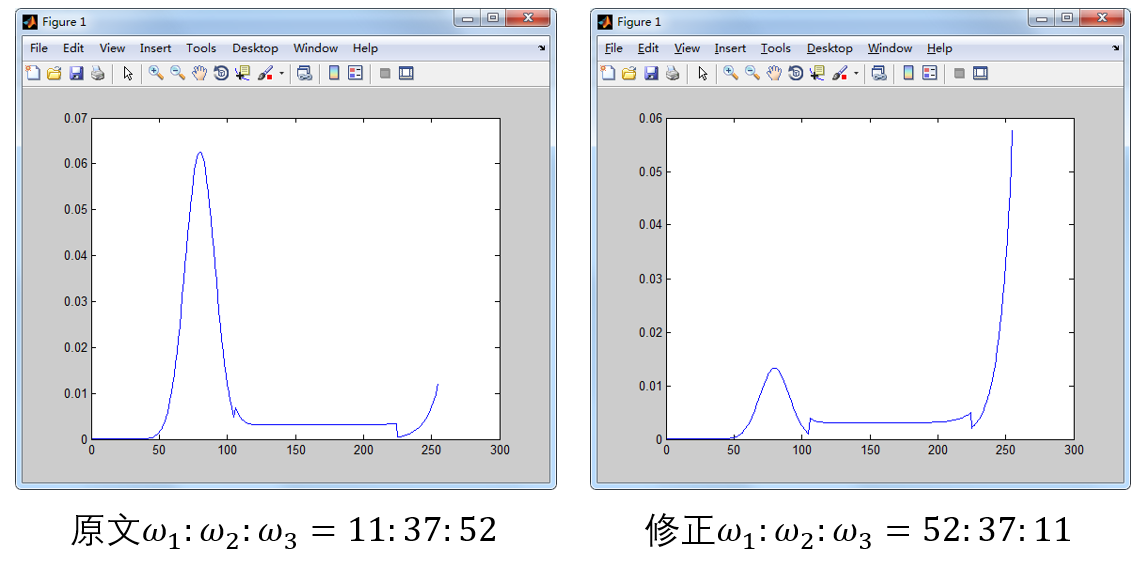
需要注意的是，上图参数学习结果（同时也是(a)中的 $\omega_i$ 比例）有误，因此需要交换 $w_1$ 与 $w_3$ (上图中全部的 $w_1$ 与 $w_3$ 都需要交换)，证明如下。

纹理绘制

纹理的绘制是最终的一步。

色调纹理(tonal texture)是指没有明显方向的线条图样，只表示色调信息。作者利用色调图学习手绘色调图样，如图所示。

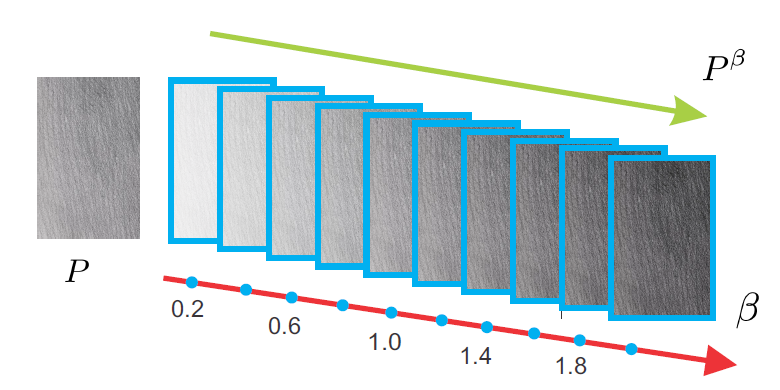
人工手绘色调纹理是在同一位置反复绘制，作者使用多层线条（multiplication of strokes）模拟这一过程，其输出表示为指数组合 $H^{β(x)}(x)≈J(x)$ 或 $β(x)\log H(x)≈\log J(x)$ ），即为拟合待转换图像 $J$ 的局部色调，将参考色调纹理 $H$ 反复绘制 $\beta$ 次。

此外，β必须满足局部平滑，可通过最小化下列方程求解：

\beta^*=\mathop{\arg \min}_\beta ||\beta \log H - \log J(x)||^2_2 +\lambda|| \nabla \beta||^2_2

其中， $\lambda$ 取0.2，上述方程可转化为标准线性方程(strand linear equation)，用共轭梯度法(conjugate gradient)求解。

最终，所绘制得到的纹理图为：

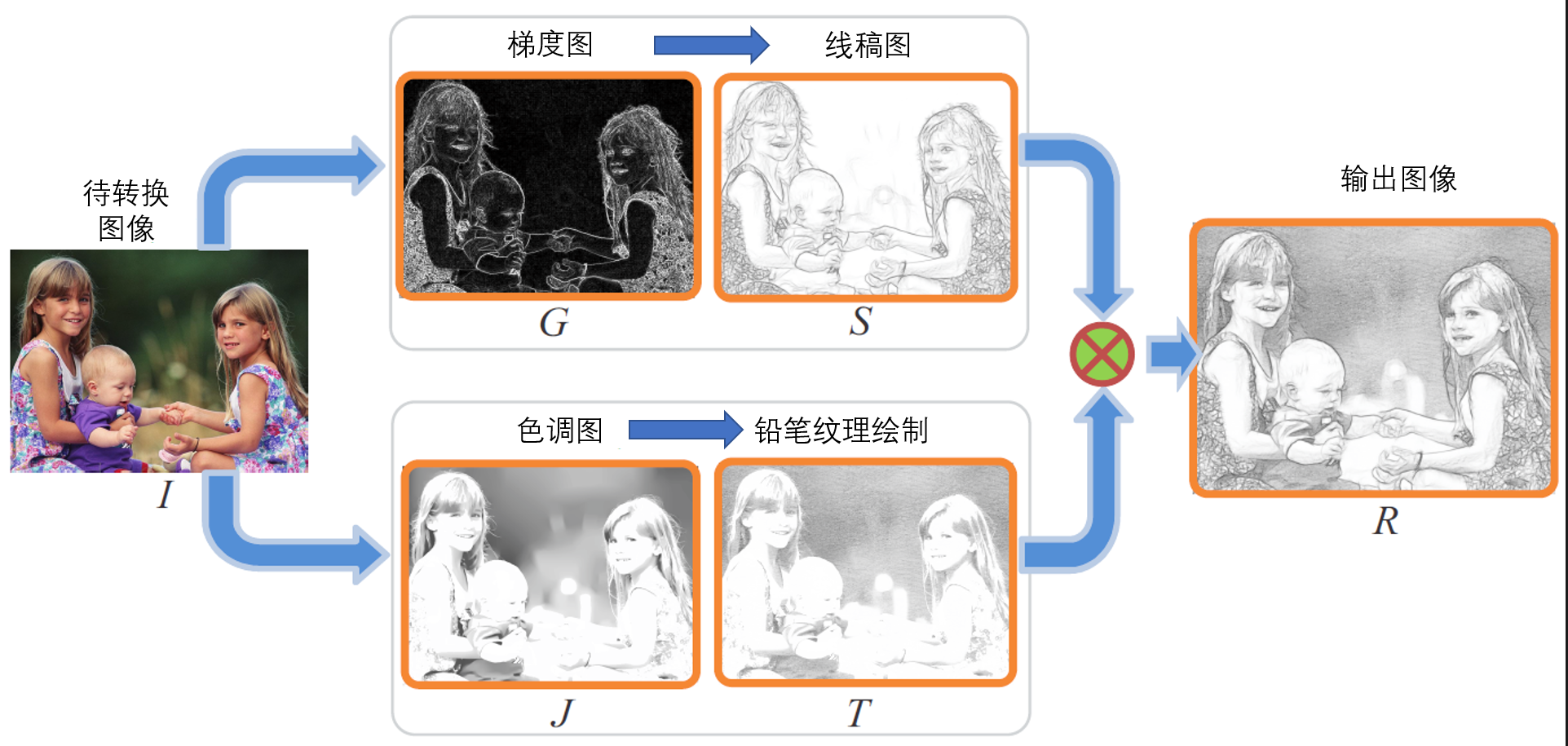
最终手绘图生成

最后一步，我们要结合线稿图和纹理图，通过纹理图和线稿图相应位置相乘得到，为：

由此，理论部分内容已经彻底介绍完毕，用一张流程图表示全部步骤帮助大家梳理思路，如下：

代码实战部分

线稿生成的代码如下

% matlab2017 a
% GenStroke.m

function S = GenStroke(im, ks, width, dirNum)
% ==============================================
%   计算图像线条结构 'S'
%  
%   参数说明
%   @im        : 输入图像，其像素值动态范围在[0,1]之间
%   @ks        : 卷积核大小
%   @width     : 生成的线稿笔画粗细
%   @dirNum    : 线条方向的数量，论文中使用的为8
%
    
    %% 初始化，计算图像大小
    [H, W, ~] = size(im);
    
    %% 平滑，此处使用了中值滤波
    im = medfilt2(im, [3 3]);
    
    %% 边缘提取，图像梯度计算
    imX = [abs(im(:,1:(end-1)) - im(:,2:end)),zeros(H,1)];
    imY = [abs(im(1:(end-1),:) - im(2:end,:));zeros(1,W)];  
    imEdge = imX + imY;

    %% 在沿着方向计算中方向上的卷积计算 
    kerRef = zeros(ks*2+1);
    kerRef(ks+1,:) = 1;

    %% 分类，对应线稿生成中的第三步
    response = zeros(H,W,dirNum);
    for n = 1 : dirNum
        ker = imrotate(kerRef, (n-1)*180/dirNum, 'bilinear', 'crop');
        response(:,:,n) = conv2(imEdge, ker, 'same');
    end

    [~, index] = max(response,[], 3); 

    %% 线条绘制
    C = zeros(H, W, dirNum);
    for n = 1 : dirNum
        C(:,:,n) = imEdge .* (index == n);
    end

    kerRef = zeros(ks*2+1);
    kerRef(ks+1,:) = 1;
    for n = 1 : width
        if (ks+1-n) > 0
            kerRef(ks+1-n,:) = 1;
        end
        if (ks+1+n) < (ks*2+1)
            kerRef(ks+1+n,:) = 1;
        end
    end
    
    Spn = zeros(H, W, dirNum);
    for n = 1 : dirNum
        ker = imrotate(kerRef, (n-1)*180/dirNum, 'bilinear', 'crop');
        Spn(:,:,n) = conv2(C(:,:,n), ker, 'same');
    end

    Sp = sum(Spn, 3);
    Sp = (Sp - min(Sp(:))) / (max(Sp(:)) - min(Sp(:)));
    S = 1 - Sp;
end

色调图生成的代码如下

% GenToneMap.m

function J = GenToneMap(im)
% ==============================================
%   计算色调图 'T'
%  
%   参数说明
%   @im        : 输入图像，其像素值动态范围在[0,1]之间
%
    
    %% 参数定义
    Ub = 225;
    Ua = 105;
    
    Mud = 90;
    
    DeltaB = 9;
    DeltaD = 11;
    
    % 第一组 以下三组为直方图明暗映射参数，我们在博客中已经解释了参数Omega1与Omega3的互换，也在这里进行了解释
%     Omega1 = 42;
%     Omega2 = 29;
%     Omega3 = 29;
    % 第二组
%     Omega1 = 52;
%     Omega2 = 37;
%     Omega3 = 11;
    % 第三组
    Omega1 = 76;
    Omega2 = 22;
    Omega3 = 2;
    
    %% 计算待转换风格图像的直方图
    histgramTarget = zeros(256, 1);
    total = 0;
    for ii = 0 : 255
        if ii < Ua || ii > Ub
            p = 0;
        else
            p = 1 / (Ub - Ua);
        end
        
        histgramTarget(ii+1, 1) = (...
            Omega1 * 1/DeltaB * exp(-(255-ii)/DeltaB) + ...
            Omega2 * p + ...
            Omega3 * 1/sqrt(2 * pi * DeltaD) * exp(-(ii-Mud)^2/(2*DeltaD^2))) * 0.01;
        
        total = total + histgramTarget(ii+1, 1);
    end
    histgramTarget(:, 1) = histgramTarget(:, 1)/total;

%     %% 中值平滑
%     im = medfilt2(im, [5 5]);
    
    %% 直方图匹配
    J = histeq(im, histgramTarget);
    
    %% 滤波平滑
    G = fspecial('average', 10);
    J = imfilter(J, G,'same');
end

局部纹理绘制的代码如下

% GenPencil.m


function T = GenPencil(im, P, J)
% ==============================================
%   计算手绘风格图 'T'
%  
%   参数说明
%   @im        : 输入图像，其像素值动态范围在[0,1]之间
%   @P         : 手绘纹理参考图像
%   @J         : 生成好的色调图
%

    %% 参数定义
    theta = 0.2; %此阈值参数是论文中给定的
    
    [H, W, ~] = size(im);

    %% 初始化
    P = imresize(P, [H, W]);
    P = reshape(P, H*W, 1);
    logP = log(P);
    logP = spdiags(logP, 0, H*W, H*W);
    
    J = imresize(J, [H, W]);
    J = reshape(J, H*W, 1);
    logJ = log(J);
    
    e = ones(H*W, 1);
    Dx = spdiags([-e, e], [0, H], H*W, H*W);
    Dy = spdiags([-e, e], [0, 1], H*W, H*W);
    
    %% 计算 A and b
    A = theta * (Dx * Dx' + Dy * Dy') + (logP)' * logP;
    b = (logP)' * logJ;
    
    %% 共轭梯度法求解
    beta = pcg(A, b, 1e-6, 60);
    
    %% 结果
    beta = reshape(beta, H, W);
    
    P = reshape(P, H, W);
    
    %% 局部纹理图计算
    T = P .^ beta;
end

运行实施例

以图像转换为手绘风格中面临的问题及分析一节中用到的抖森图像为例。

% ==============================================
%   参数说明
%   @im        : 输入图像
%   @ks        : 卷积线的长度
%   @width     : 线稿图中线条的宽度
%   @dirNum    : 方向数
%   @gammaS    : 线条的暗度
%   @gammaI    : 手绘风格转换完成后图像的暗度

%% 初始化
clc
clear
close all
im = imread('C:\Users\as\Desktop\juejin\IMG_4511.png');
ks=8;
width=1; 
dirNum=8; 
gammaS=1.0; 
gammaI=1.0;
figure
imshow(im)

%% 预处理
im = im2double(im);
[H, W, sc] = size(im);

%% 对于彩色图像，将RGB转换至YUV颜色空间。
% 这一点在论文中有简单提及，即将RGB转为YUV，并单独在Y亮度通道上执行论文中的所有操作，
% 最终将处理的YUV转换回RGB，即得到彩色手绘图像
% 此处的只有Y经过处理，UV为YUV颜色空间中表示色度的分量，故不改动
if (sc == 3)
    yuvIm = rgb2ycbcr(im);
    lumIm = yuvIm(:,:,1);
else
    lumIm = im;
end

%% 生成线稿图
S = GenStroke(lumIm, ks, width, dirNum) .^ gammaS; % 用伽马矫正使结果变暗
figure, imshow(S)

%% 生成色调图 (tonemap)
J = GenToneMap(lumIm) .^ gammaI; % 用伽马矫正使结果变暗
figure, imshow(J)

%% 读入参考手绘纹理图
P = im2double(imread('C:\Users\as\Desktop\juejin\pencil.jpg'));
P = rgb2gray(P);
figure, imshow(P)

%% 生成待转换图像的手绘纹理图
T = GenPencil(lumIm, P, J);
figure, imshow(T)

%% 计算结果
lumIm = S .* T;

if (sc == 3)
    yuvIm(:,:,1) = lumIm;
%     resultIm = lumIm;
    I = ycbcr2rgb(yuvIm);
else
    I = lumIm;
end

figure, imshow(I)

上面这幅图像就是代码运行的最终结果。而如果我们将参数gammaI设置为5.0，则会得到这样的结果。

相关代码皆在上文给出，因此参数的调试与结果本文不会着重讨论，初始参数即为论文实验部分的参数。

我们可以看看真实手绘图像与算法风格转换图像的结果对比。

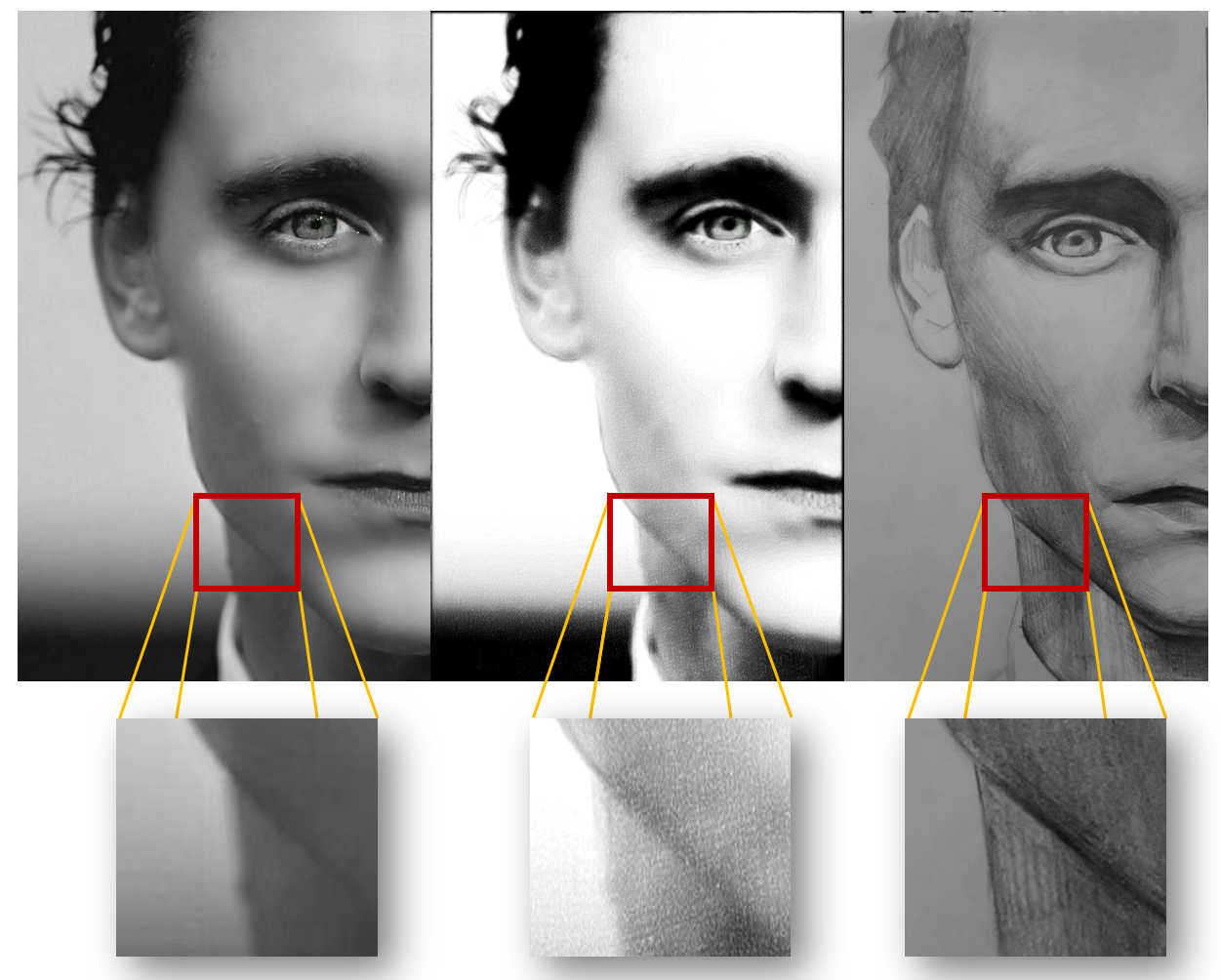
代码结果能够更保真的还原图像的形状信息，同时，人像并非最适合手绘风格迁移的测试图像，算法在建筑、风景中的表现会更好，如下图。

从左到右依次为：原图，线稿图，经局部纹理绘制的色调图，以及最终结果。效果非常显著，这种图像处理算法已经达到了"欺骗眼睛"的作用。如果你将最终结果图给别人看，基本不会有人怀疑这张图是通过真实图像转换得到的。

所存在的问题分析

该方法是存在参数依赖的问题的，比如参数不当时引起的脱色，如下图采用的是论文实验参数，却因直方图匹配的原因导致脱色。

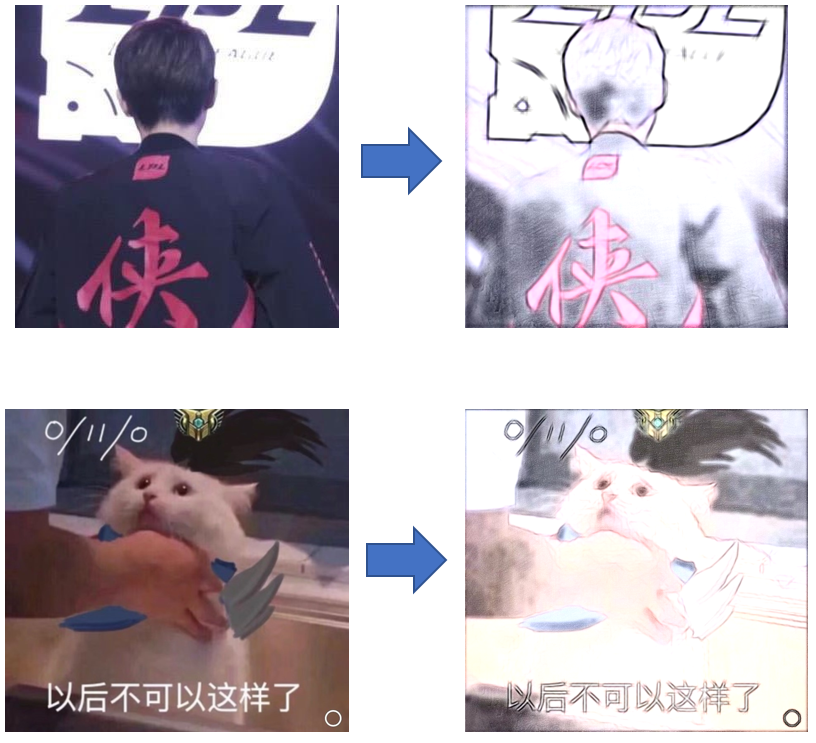
上图中，"侠"字右上角的衣服，头发的颜色以及手臂的颜色，在结果图像中有非常显著的撕裂与脱色，而原图的变化是平滑的，这些问题的直接原因在于直方图匹配的环节中，有直方图的强制拉伸步骤。而根本原因在于，先验的方法从本质上存在局限性，在该问题的表现中即为：若图像的直方图与常规的自然图像（参考色调转移与局部纹理绘制一节中的(d) histogram of(a)）存在非常大的差异，则会造成诸如此类的问题。

另一个在测试图像中出现问题的现象是该方法对于图像边缘的卷积上的，由于需要形成手绘时的交叉线与断裂线，多数边缘区域都会生成线条，而产生如下图所示的问题。

嘴唇上的高亮反射区域被绘制了黑色线条，而眼睛、头发等边缘密集部分产生了不同程度的噪声。

参考文献

最后附上论文链接，有兴趣的朋友可以自行研究。 paper on Combining Sketch and Tone for Pencil Drawing Production:www.cse.cuhk.edu.hk/~leojia/pro…

如果你喜欢我的这篇博客的话，请点个赞吧！~如果你喜欢我的风格并且想了解更多相关的内容，可以关注我~我会不定期更新有趣的图像与视觉方面的知识并加入个人的独特理解~

您的支持就是对我最大的肯定。