分析
首先队列中的第一个人必须持有50元面额,否则的话在第一个人这里就已经无法找开了;第二个人可以持有100元,此时刚好可以找开,也可以持有50元,此时可以保证第三、四个人即使持有的是100元也可以找开。可以发现,要使得“可以找开”的状态持续到第100个人,在任意一个位置及其之前的所有人中,持有50元的人数不少于持有100元的人数。
定义:持有100元的人为“1”,持有50元的为“-1”,产生100个两点分布的随机数,计算累计和,当所有位置的累计和都小于等于0时,该队列满足要求,可以“一直都能找开”;否则,必然在队列的某个位置无零钱可找。
定义模拟队列并求概率的函数:
PassProb <- function(money100_num, money50_num, R)
{
s <- money100_num + money50_num
array <- replicate(R, sample(c(rep(1, money100_num), rep(-1, money50_num)),s)) # 生成R个随机队列
cs <- apply(array, 2, cumsum) # 累加
isPass <- apply(cs, 2, function(x){ all(x <= 0) }) # 任意位置,累计持有100元的人数多于50元的,就找不开零钱
sum(isPass)/R # 计算频率
}
money100_num <- 40 # 持有百元大钞的人数
money50_num <- 60 # 持有50元的人数
R <- 1e5 # 模拟队列数
PassProb(money100_num, money50_num, R)
重复模拟10000 次:
money100_num <- 40 # 持有百元大钞的人数
money50_num <- 60 # 持有50元的人数
R <- 1e5 # 模拟队列数
PassProb(money100_num, money50_num, R)
# [1] 0.34378
#---------------------------------------------------------
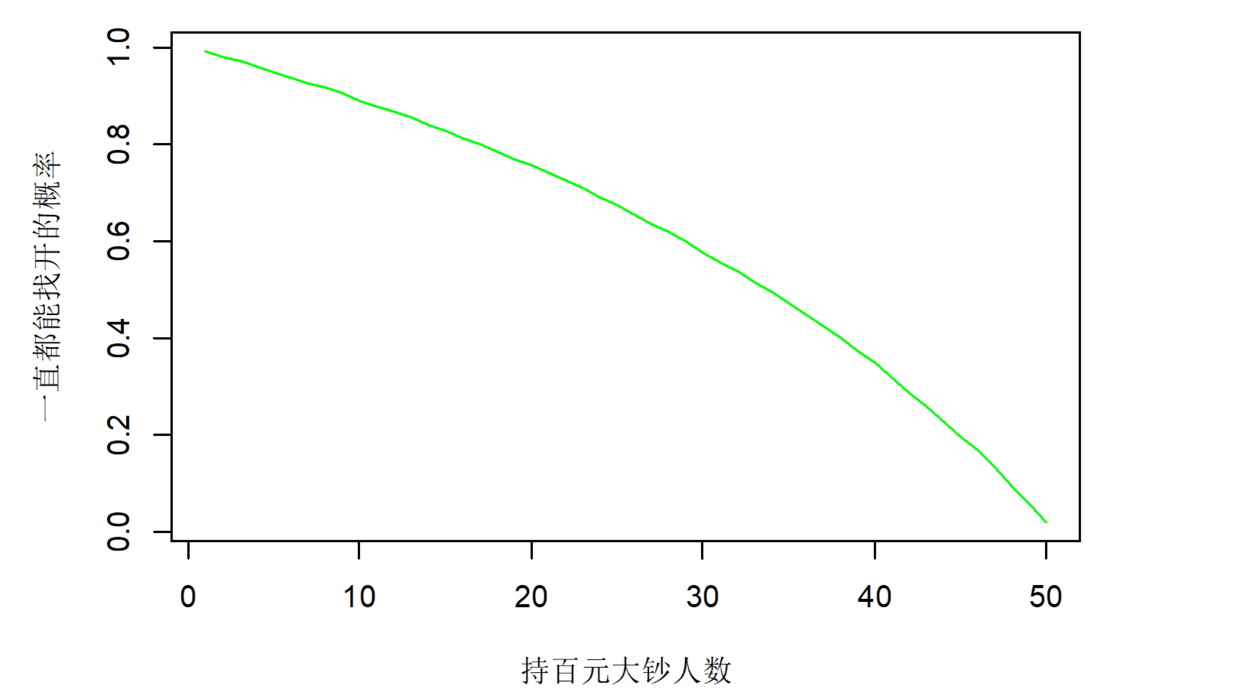
money100_num_vec <- 1:50
money50_num_vec <- 100 - money100_num_vec
R <- 1e5
prob <- rep(NA, 50)
for (i in money100_num_vec)
{
prob[i] <- PassProb(money100_num_vec[i], money50_num_vec[i], R)
}
plot(money100_num_vec, prob, col="green", type="l",
xlab="持百元大钞人数", ylab="一直都能找开的概率")