图像缩放时存在的问题
相信大家曾经见到过这样的问题,图像需要因为显示尺寸的问题需要进行适应尺寸而进行的变换,非常简单粗暴的一种方式就是拉伸,但是效果不尽人意,以博主本人的显示器为例,见下图。
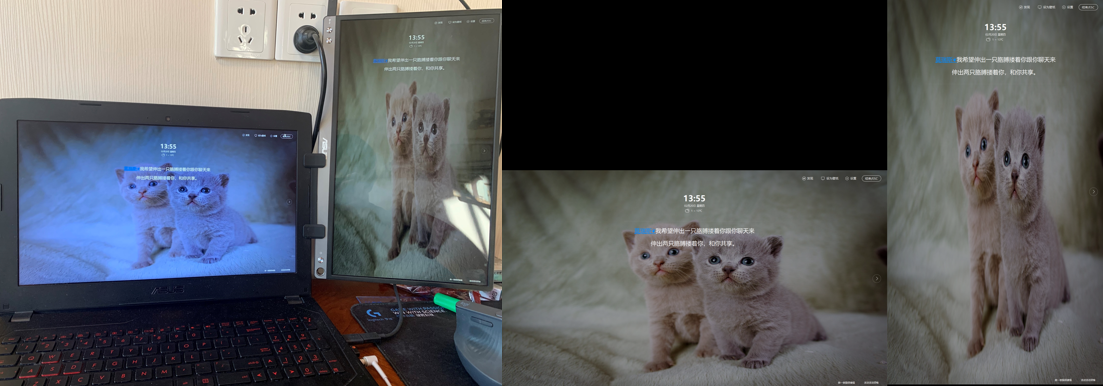
事实上,图像缩放是随处可见的,同一张图片在不同的显示设备间显示(比如不同显示屏尺寸比例的手机)时就会遇到图像缩放的问题。举个更常见易懂的例子来说,在电影拍摄时所保存的尺寸和电影院影厅荧幕的尺寸往往是不匹配的,这就要求对尺寸进行缩放。
最容易想到的解决方案(暴力解法)是上图中出现图像拉伸,虽然结果稀烂,但是就目的而言已经达成了。但如果你是在看电影时遇到了经过暴力拉伸处理的影片,我个人认为应该得不到比较好的观影体验,至少影响了正常的观感。因此,图像缩放问题的各种处理方法也就应运而生了。
Letterbox 与 Pillarbox
Letterbox与Pillarbox的名字非常形象,信箱(Letterbox)与信筒(Pillarbox)。


同理,Pillarbox是低长宽比图像在在高长宽比显示设备上使用的方法,在视频的两边用黑框填充,就不过多解释了。
Pan&Scan
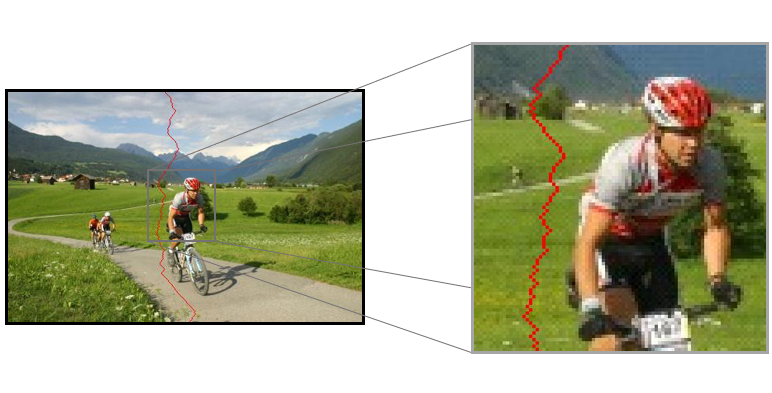
Pan&Scan是一种在影视作品进行转录的时候仍然会使用的方法,比如在4:3的设备(比如不够长的电影荧幕)上显示16:9的图像(比如非常长的电影画面,这个长指的是画面的水平长度)时,使图像与设备同高(竖直方向上长度相同),在水平方向多余的图像会被截断,截取的范围可根据中心点偏移来调整。

如下图所示,深色区域为与显示尺寸比例相同的截取框,而浅色部分与深色部分两部分合并就是待剪取的原始画面,就像有一个框在滑动扫描,因此被称为Pan & Scan。通过搜索损失信息最少的截取区域实现合适的缩放。

paper on pan&scan: graphics.cs.wisc.edu/Papers/2006…
像素移除
与前面三种方法相比,像素移除终于有点图像处理的意思了,其思想也相对比较容易理解。如果图像的重要内容在两侧,裁剪一定无法同时保留两个重要内容,那万一有哪个奇怪的甲方
在极端情况下需要有这样的效果,岂不是只能用PS了?诚然,看似不可能,实际上还是有点可能性的,那就是 像 素 剔 除。
由于像素与像素之间是有空间相关性的,所以如果要进行图像压缩,舍弃某几行(或几列)不重要的(不重要即指梯度信息少的区域)像素的压缩效果其实还是比较可观的,如图所示。

图中上方位置的是原图,热度图是梯度图像,右下角的图像是经过像素剔除后的结果(选择每一列梯度信息累加最少的结果并循环剔除的结果),其实效果还可以了(昧着良心)。
Seam Carving
兜了4个圈(标)子(题)终于到了本文的重点方法了!效果可谓神奇的图像缩放算法,Seam Carving。
上来先甩论文链接 paper on seam carving: graphics.cs.cmu.edu/courses/15-…
在Pan&Scan中讲到,我们可以以图像的梯度信息来判别主要的重要内容。


Seam Carving Algorithm
- 假设:只需要对一个方向进行裁剪。
- 基本的想法:去除图像中“不重要的像素点”
- 基于梯度作为能量函数
- 保留了轮廓
- 人类视觉对边缘信息更加敏感 ——因此可以从平滑的区域里移除内容
- 算法简单,思想易懂,但能产生很好的结果
- 从上到下(或从左到右)的一条由像素点组成的 路径 。每一行仅仅包含一个像素并且上下两行像素路径的水平移动小于等于1
数学描述如下
而Seam carving的目标就是找到最佳路径的Seam
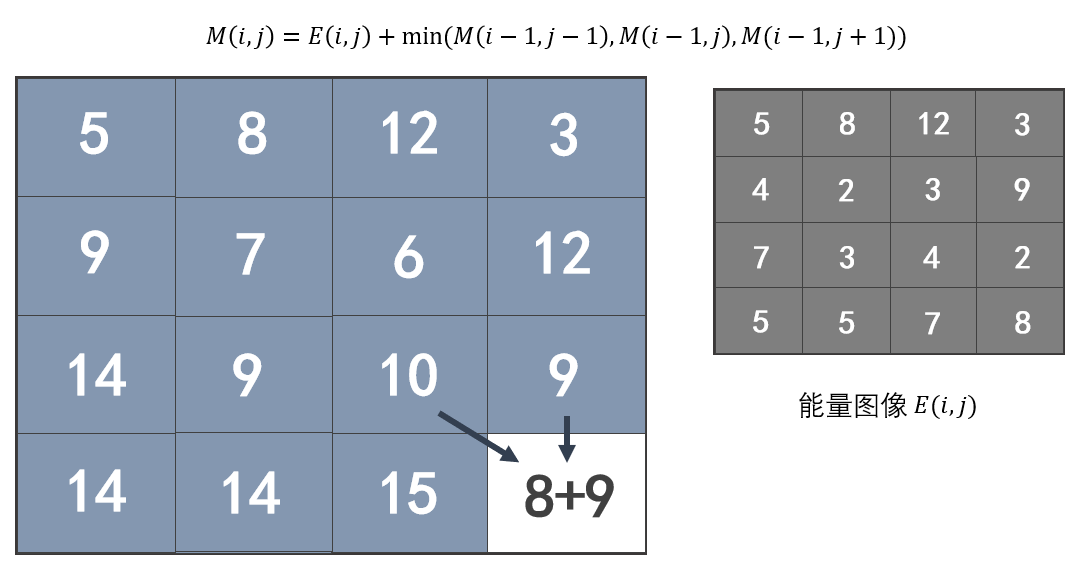
我们可以基于动态规划算法,利用递归关系进行求解,如下式。
能量损失的累加如下图所示更容易理解
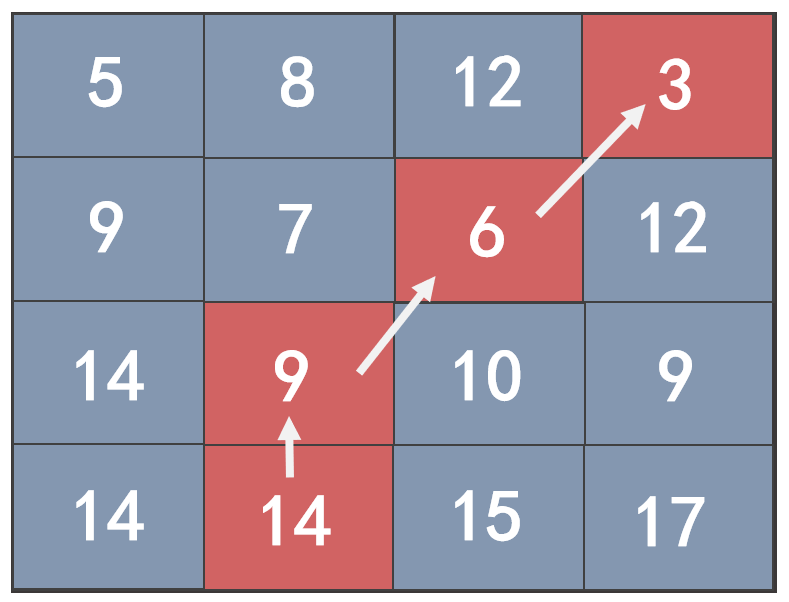
算法伪代码如下图所示。

放一些令人惊叹的处理结果~



代码实战部分
# Python
# seam_carving.py
import numpy as np
from skimage import color
def energy_function(image):
"""Computes energy of the input image.
对于每个像素,先计算它 x- 和 y- 方向的梯度,然后再把它们的绝对值相加。
记得先把彩色图像转成灰度图像哦。
Hint: 这里可以使用 np.gradient
Args:
image: 图片 (H, W, 3)
Returns:
out: 每个像素点的energy (H, W)
"""
H, W, _ = image.shape
out = np.zeros((H, W))
gray_image = color.rgb2gray(image)
### YOUR CODE HERE
out1,out2= np.gradient(gray_image)
out1 = np.abs(out1)
out2 = np.abs(out2)
out = out1 + out2
### END YOUR CODE
return out
def compute_cost(image, energy, axis=1):
"""这一步从图片的顶部到低端,求取最小cost的路径
从第一行开始,计算每一个像素点的累积能量和,即cost。像素点的cost定义为从顶部开始,同一seam上像素点的累积能量和的最小值.
同时,我们需要返回这条路径。路径上的每个像素点的值只有三种可能:-1,0,以及1,-1表示当前像素点与它的左上角的元素相连,0表示当前像素点
与它正上方的元素相连,而1表示当前像素点与它右上方的元素相连。
比如,对于一个3*3的矩阵,如果点(2,2)的值为-1, 则表示点(2,2)与点(1,1)相连接。
当能量相同的时候,我们规定选取最左边的路径。注意,np.argmin 函数可以返回最小值在数组中所在的位置(索引值)。
提示:由于这个函数会被大量使用,如果循环过多的话,会使程序运行速度变慢的.
正常情况下,你只会进行一次列循环,而不会对每一行的元素进行循环。
假如你现在是对(i,j)号元素求cost,那么(i,j)号元素只可能与(i-1,j-1)、(i-1,j),或者(i-1,j+1)号元素相连,并且是其中的最小者。
为了避免对每一行的元素都进行循环,我们可以进行向量化操作。
举例:假设我们的energy = [1, 2, 3; 4, 5, 6],现在我们需要确定第二行元素[4, 5, 6]分别是和第一行的哪几个元素相连接,那么我们
只需要构造一个新的矩阵M = [∞, 1, 2;1, 2, 3;2, 3, ∞];矩阵M的第一列代表元素4的可能对应的三个元素,即:[无穷大,1,2];第二列
代表元素5可能对应的三个元素,即[1, 2, 3];第三列代表元素6可能对应的三个元素,即[2, 3, 无穷大]。
通过这种方式,我们只需要对矩阵M沿着竖直方向求一次最小值,就可以把第二行所对应的元素全部都求出来了。避免了对每一行的元素进行循环。
同时,可以利用np.argmin函数一次性地把path求出来
参数:
image: 该函数里面没有使用
(留在这是为了和 compute_forward_cost 函数有一个相同的接口)
energy: 形状为 (H, W) 的数组
axis: 确定沿着哪个轴计算(axis=1为水平方向,axis=0为竖直方向)
返回值:
cost: 形状为 (H, W) 的数组
paths: 形状为 (H, W) 的数组,数组元素为 -1, 0 或者1
"""
energy = energy.copy()
if axis == 0:
energy = np.transpose(energy, (1, 0))
H, W = energy.shape
cost = np.zeros((H, W))
paths = np.zeros((H, W), dtype=np.int)
# 初始化
cost[0] = energy[0]#第一行的cost就是它本身
paths[0] = 0 # 对于第一行,我们并不在意
### YOUR CODE HERE
for i in range(1,H):
M=np.zeros((3,W))
M[0][0]=float('inf')
M[0,1:]=cost[i-1,:W-1]
M[1,:]=cost[i-1,:]
M[2,:W-1]=cost[i-1,1:]
M[2][W-1]=float('inf')
cost[i]=np.min(M,0)+energy[i]
paths[i]=np.argmin(M,0)-1
### END YOUR CODE
if axis == 0:
cost = np.transpose(cost, (1, 0))
paths = np.transpose(paths, (1, 0))
# 确定路径只包含 -1, 0 或者 1
assert np.all(np.any([paths == 1, paths == 0, paths == -1], axis=0)), \
"paths contains other values than -1, 0 or 1"
return cost, paths
def backtrack_seam(paths, end):
"""从paths图中找出我们所需要的seam
为了实现这个功能,我们需要从图像的最下面一行开始,沿着paths图所给定的方向找出整个seam:
- 左上方 (-1)
- 正上方 (0)
- 右上方 (1)
参数:
paths: 形状为 (H, W) 的数组,每个元素都是 -1, 0 或者 1
end: seam的终点,即最下面一行中累积能量cost最小的像素点位置
Returns:
seam: 形状为 (H,)的数组,数组的第i个元素保存了第i行的索引值。即seam里面每个元素的位置都是(i, seam[i])。
"""
H, W = paths.shape
# 用-1来进行初始化,确保每个元素都被正确赋值(如果没被赋值,值仍为-1,而-1是一个无效的索引)
seam = - np.ones(H, dtype=np.int)
# 最后一个元素
seam[H-1] = end
G=np.ones(H, dtype=np.int)
a=np.ones(H, dtype=np.int)
### YOUR CODE HERE
for i in range(H-1,0,-1):
if paths[i][seam[i]]==-1:
seam[i-1]=seam[i]-1
if paths[i][seam[i]]==0:
seam[i-1]=seam[i]
if paths[i][seam[i]]==1:
seam[i-1]=seam[i]+1
### END YOUR CODE
# 确定seam里面只包含[0, W-1]
assert np.all(np.all([seam >= 0, seam < W], axis=0)), "seam contains values out of bounds"
return seam
def remove_seam(image, seam):
"""从图像中移除一条seam,即用原图像image来填充输出图像out.
本函数会在 reduce 函数以及 reduce_forward 函数里面用到.
参数:
image: 形状为 (H, W, C) 或者 (H, W) 的数组
seam: 形状为 (H,)的数组,数组的第i个元素保存了第i行的索引值。即seam里面每个元素的位置都是(i, seam[i])。
返回值:
out: 形状为 (H, W - 1, C) 或者 (H, W - 1) 的数组
请确保 `out` 和 `image` 的类型相同
"""
# 如果是2维的图像(灰度图),则增加维度,即变为 (H, W, 1)的图像
if len(image.shape) == 2:
image = np.expand_dims(image, axis=2)
out = None
H, W, C = image.shape
out = np.zeros((H, W - 1, C), dtype=image.dtype) # 每一行删除一个像素
### YOUR CODE HERE
for i in range(H):
for j in range(W-1):
if j<seam[i]:
out[i][j]=image[i][j]
if j>=seam[i]:
out[i][j]=image[i][j+1]
### END YOUR CODE
out = np.squeeze(out) # 把shape为1的维度去掉。也就是说,如果前面维度增加了,则把增加的维度去掉
# 确保 `out` 和 `image` 的类型相同
assert out.dtype == image.dtype, \
"Type changed between image (%s) and out (%s) in remove_seam" % (image.dtype, out.dtype)
return out
def reduce(image, size, axis=1, efunc=energy_function, cfunc=compute_cost):
"""利用 seam carving算法减少图像的尺寸.
每次循环我们都移除能量最小的seam. 不断循环这个操作,知道得到想要的图像尺寸.
利用到的函数:
- efunc
- cfunc
- backtrack_seam
- remove_seam
Args:
image: 形状为 (H, W, 3) 的数组
size: 目标的高或者宽 (由 axis 决定)
axis: 减少宽度(axis=1) 或者高度 (axis=0)
efunc: 用来计算energy的函数
cfunc: 用来计算cost的函数(包括backtrack 和 forward两个版本),直接利用 cfunc(image, energy) 来调用cfunc计算cost。默认为compute_cost
Returns:
out: 如果axis=0,则输出尺寸为 (size, W, 3),如果 axis=1,则输出尺寸为 (H, size, 3)
"""
out = np.copy(image)
if axis == 0:
out = np.transpose(out, (1, 0, 2))
H = out.shape[0]
W = out.shape[1]
assert W > size, "Size must be smaller than %d" % W
assert size > 0, "Size must be greater than zero"
### YOUR CODE HERE
while(out.shape[1]>size):
energy = efunc(out)
vcost,vpaths=cfunc(out, energy)
end = np.argmin(vcost[-1])
seam = backtrack_seam(vpaths, end)
out=remove_seam(out, seam)
### END YOUR CODE
assert out.shape[1] == size, "Output doesn't have the right shape"
if axis == 0:
out = np.transpose(out, (1, 0, 2))
return out
def duplicate_seam(image, seam):
"""复制seam上的像素点, 使得这些像素点出现两次.
该函数会被 enlarge_naive 以及 enlarge 调用。
参数:
image: 形状为 (H, W, C) 的数组
seam: 形状为 (H,)的数组,数组的第i个元素保存了第i行的索引值。即seam里面每个元素的位置都是(i, seam[i])。
Returns:
out: 形状为 (H, W + 1, C) 的数组
"""
if len(image.shape) == 2:
image = np.expand_dims(image, axis=2)
H, W, C = image.shape
out = np.zeros((H, W + 1, C))
### YOUR CODE HERE
for i in range(H):
for j in range(W+1):
if j<=seam[i]:
out[i][j]=image[i][j]
if j>seam[i]:
out[i][j]=image[i][j-1]
### END YOUR CODE
return out
def enlarge_naive(image, size, axis=1, efunc=energy_function, cfunc=compute_cost):
"""复制seam,用以增加图像的尺寸.
每次循环,我们都会复制图像中能量最低的seam. 不断重复这个过程,知道图像尺寸满足要求.
用到的函数:
- efunc
- cfunc
- backtrack_seam
- duplicate_seam
Args:
image: 形状为 (H, W, C) 的数组
size: 目标的高或者宽 (由 axis 决定)
axis: 增加宽度(axis=1) 或者高度 (axis=0)
efunc: 用来计算energy的函数
cfunc: 用来计算cost的函数(包括backtrack 和 forward两个版本),直接利用 cfunc(image, energy) 来调用cfunc计算cost。默认为compute_cost
Returns:
out: 如果axis=0,则输出尺寸为 (size, W, C),如果 axis=1,则输出尺寸为 (H, size, C)
"""
out = np.copy(image)
if axis == 0:
out = np.transpose(out, (1, 0, 2))
H = out.shape[0]
W = out.shape[1]
assert size > W, "size must be greather than %d" % W
### YOUR CODE HERE
while(out.shape[1]<size):
energy = efunc(out)
vcost,vpaths=cfunc(out, energy)
end = np.argmin(vcost[-1])
seam = backtrack_seam(vpaths, end)
out=duplicate_seam(out, seam)
### END YOUR CODE
if axis == 0:
out = np.transpose(out, (1, 0, 2))
return out
def find_seams(image, k, axis=1, efunc=energy_function, cfunc=compute_cost):
"""找出图像中能量最小的k条seam.
我们可以按照移除的方式把前k条seam记录下来,然后利用函数enlarge把它们复制一遍。
但这样存在一个问题,每次在图片中移除一条seam以后,像素的相对位置会发生改变,因此无法直接进行移除。
为了解决这个问题,这里我们定义了两个矩阵,seams以及indices。seams的尺寸和原图像保持一致,用以记录每次移除的seam在原始图片中的位置。
而indices矩阵和图像image一起,随着seam的移除逐渐变小,它用来记录每次移除的seam在image中的位置。同时,我们也用它来追踪seam在原始图片中的位置。
用到的函数:
- efunc
- cfunc
- backtrack_seam
- remove_seam
参数:
image: 形状为 (H, W, C) 的数组
k: 需要寻找的seam的数目
axis: 是在宽度(axis=1) 或者高度 (axis=0)上寻找
efunc: 用来计算energy的函数
cfunc: 用来计算cost的函数(包括backtrack 和 forward两个版本),直接利用 cfunc(image, energy) 来调用cfunc计算cost。默认为compute_cost
返回值:
seams: 尺寸为 (H, W) 的数组
"""
image = np.copy(image)
if axis == 0:
image = np.transpose(image, (1, 0, 2))
H, W, C = image.shape
assert W > k, "k must be smaller than %d" % W
# 生成indices矩阵来记住原始像素点的索引
# indices[row, col] 表示的是当前像素点的col值。
# 也就是说,该像素点[ro2, col]对应于原始图片中的(row, indices[row, col])
# 通过这样子操作,我们用像素值记录下了像素的坐标,由于row的值是不会改变的,因此即使在移除seam的过程中
# 我们也能从seam里面追踪原始的像素点
# 示例,对于一个形状为(2, 4)的图像,它所对应的初始的`indices` 矩阵的形状是:
# [[0, 1, 2, 3],
# [0, 1, 2, 3]]
indices = np.tile(range(W), (H, 1)) # 尺寸为 (H, W) 的数组
# 我们用seams数组记录下被删除的seam
# 在seams数组中,第i条seam将会记录成值为i+1的像素(seam的序号从0开始)
# 例如,一幅(3, 4) 的图片的前两个seams数组可能如下表示:
# [[0, 1, 0, 2],
# [1, 0, 2, 0],
# [1, 0, 0, 2]]
# 可以看到,值为1或者值为2的像素点可以构成一条seam
seams = np.zeros((H, W), dtype=np.int)
# 循环找到k条seam
for i in range(k):
# 获取当前最佳的seam,你可以和你前面写的函数比较一下是否一样
energy = efunc(image)
cost, paths = cfunc(image, energy)
end = np.argmin(cost[H - 1])
seam = backtrack_seam(paths, end)
# 移除当前的这条seam
image = remove_seam(image, seam)
# 在图像中用i+1保存下这条seam
# 查看这条seam通过的路径是否全为0
assert np.all(seams[np.arange(H), indices[np.arange(H), seam]] == 0), \
"we are overwriting seams"
seams[np.arange(H), indices[np.arange(H), seam]] = i + 1
# 同时,我们在indices这个数组里面移除seam,使得它的形状与image形状保持一致
indices = remove_seam(indices, seam)
if axis == 0:
seams = np.transpose(seams, (1, 0))
return seams
def enlarge(image, size, axis=1, efunc=energy_function, cfunc=compute_cost):
"""通过复制低能量的seams,我们可以放大图片.
首先,我们通过函数find_seams来获取k条低能量的seams.
随后我们循环k次来复制这些seams.
利用了函数:
- find_seams
- duplicate_seam
参数:
image: 形状为 (H, W, C) 的数组
size: 目标的尺寸(宽度或者高度)
axis: 是在宽度(axis=1) 或者高度 (axis=0)上寻找
efunc: 用来计算energy的函数
cfunc: 用来计算cost的函数(包括backtrack 和 forward两个版本),直接利用 cfunc(image, energy) 来调用cfunc计算cost。默认为compute_cost
Returns:
out: 如果axis=0,则输出为尺寸为 (size, W, C) 的数组。如果axis=1,则输出为 (H, size, C) 的数组
"""
out = np.copy(image)
# 判断是否需要转置
if axis == 0:
out = np.transpose(out, (1, 0, 2))
H, W, C = out.shape
assert size > W, "size must be greather than %d" % W
assert size <= 2 * W, "size must be smaller than %d" % (2 * W)
### YOUR CODE HERE
K=size-W
seams=find_seams(out, K)
for k in range(K):
seam = - np.ones(H, dtype=np.int)
for i in range(H):
for j in range(W+k):
if k+1==seams[i][j]:
seam[i]=j
out=duplicate_seam(out, seam)
seams=duplicate_seam(seams, seam)
### END YOUR CODE
if axis == 0:
out = np.transpose(out, (1, 0, 2))
return out
def compute_forward_cost(image, energy):
"""计算 forward cost map (竖直) 以及对应的seams的paths.
从第一行开始,计算每一个像素点的累积能量和,即cost。像素点的cost定义为从顶部开始,同一seam上像素点的累积能量和的最小值.
同时,请确保已经在原cost的基础上,增加了由于移除pixel所引入的新的能量。
与之前一样,我们需要返回这条路径。路径上的每个像素点的值只有三种可能:-1,0,以及1,-1表示当前像素点与它的左上角的元素相连,0表示当前像素点
与它正上方的元素相连,而1表示当前像素点与它右上方的元素相连。
参数:
image: 该函数里面没有使用
(留在这是为了和 compute_forward_cost 函数有一个相同的接口)
energy: 形状为 (H, W) 的数组
返回值:
cost: 形状为 (H, W) 的数组
paths: 形状为 (H, W) 的数组,数组元素为 -1, 0 或者1
"""
image = color.rgb2gray(image)
H, W = image.shape
cost = np.zeros((H, W))
paths = np.zeros((H, W), dtype=np.int)
# 初始化
cost[0] = energy[0]
for j in range(W):
if j > 0 and j < W - 1:
cost[0, j] += np.abs(image[0, j+1] - image[0, j-1])
paths[0] = 0 # 我们不用考虑paths矩阵的第一行元素
### YOUR CODE HERE
for i in range(1,H):
m1 = np.insert(image[i, 0:W - 1], 0, 0, axis=0)
m2 = np.insert(image[i, 1:W], W - 1, 0, axis=0)
m3 = image[i - 1]
v = abs(m1 - m2)
v[0] = 0
v[-1] = 0
l = v + abs(m3 - m1)
r = v + abs(m3 - m2)
l[0] = 0
r[-1] = 0
i1 = np.insert(cost[i - 1, 0:W - 1], 0, 1e10, axis=0)
i2 = cost[i - 1]
i3 = np.insert(cost[i - 1, 1:W], W - 1, 1e10, axis=0)
C = np.r_[i1 + l, i2 + v, i3 + r].reshape(3, -1)
cost[i] = energy[i] + np.min(C, axis=0)
paths[i] = np.argmin(C, axis=0) - 1
### END YOUR CODE
# 确保paths里面只包含 -1, 0 or 1
assert np.all(np.any([paths == 1, paths == 0, paths == -1], axis=0)), \
"paths contains other values than -1, 0 or 1"
return cost, paths
运行实例
# 初始化配置
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rc
from skimage import color
from skimage import io, util
from time import time
from IPython.display import HTML
import seam_carving
%matplotlib inline
plt.rcParams['figure.figsize'] = (30.0, 24.0) # 设置默认尺寸
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 自动重装外部模块
%load_ext autoreload
%autoreload 2
# 载入图片
img = io.imread('imgs/wave.jpg')
img = util.img_as_float(img)
plt.title('Original Image')
plt.imshow(img)
plt.show()

# 计算图像能量
energy = energy_function(img)
plt.title('Energy')
plt.axis('off')
plt.imshow(energy)
plt.show()

# 竖直方向的能量损耗
start = time()
vcost, _ = compute_cost(_, energy, axis=1) # 不需要第一个参数
end = time()
print("Computing vertical cost map: %f seconds." % (end - start))
plt.title('Vertical Cost Map')
plt.axis('off')
plt.imshow(vcost, cmap='inferno')
plt.show()

# 水平方向的能量损耗
start = time()
hcost, _ = compute_cost(_, energy, axis=0)
end = time()
print("Computing horizontal cost map: %f seconds." % (end - start))
plt.title('Horizontal Cost Map')
plt.axis('off')
plt.imshow(hcost, cmap='inferno')
plt.show()

利用我们在上面所找到的cost map,我们可以确定出图像里面能量最小的seam. 随后我们可以移除这条seam, 并且重复这一步直到得到我们想要的图像尺寸。
# 减少图像的宽度
H, W, _ = img.shape
W_new = 400
start = time()
out = reduce(img, W_new)
end = time()
print("Reducing width from %d to %d: %f seconds." % (W, W_new, end - start))
plt.subplot(2, 1, 1)
plt.title('Original')
plt.imshow(img)
plt.subplot(2, 1, 2)
plt.title('Resized')
plt.imshow(out)
plt.show()
seam carving缩放结果如下


也可以在水平方向上执行seam carving算法
# 减少图像的高度
H, W, _ = img.shape
H_new = 300
start = time()
out = reduce(img, H_new, axis=0)
end = time()
print("Reducing height from %d to %d: %f seconds." % (H, H_new, end - start))
plt.subplot(1, 2, 1)
plt.title('Original')
plt.imshow(img)
plt.subplot(1, 2, 2)
plt.title('Resized')
plt.imshow(out)
plt.show()

图像扩大
我们同样可以反向解决问题,也就是扩大图片,一个最简单的方法是我们不断重复地添加能量最小的seam(被使用过的seam则不能再次使用),直到尺寸符合我们的要求。
W_new = 750
start = time()
out = enlarge(img, W_new)
end = time()
# 大概需要20s
print("Enlarging width from %d to %d: %f seconds." \
% (W, W_new, end - start))
plt.subplot(2, 1, 1)
plt.title('Original')
plt.imshow(img)
plt.subplot(2, 1, 2)
plt.title('Resized')
plt.imshow(out)
plt.show()
原图

扩大后的图像

我一直认为深度学习中许多模型都是黑箱模型,你看不到数据在其中的变化,为什么用这个网络模型会比用另一个网络模型准确率更高是困扰了我挺久的问题....大概是我水平还没到家。
而seam carving算法通过简单的数学模型和思想,展示了非常漂亮的研究方法论和结果,一如在《万物理论》中,小雀斑饰演的霍金所说的那句:Wouldn't that be nice,Professor? With one simple elegant equation to explain everything.
其实seam carving还有诸多的优化空间,如通过Forward energy构建的图像边缘更平滑,由于刹不住车写了太多,再展开篇幅写可能读者也不一定有足够的精力看,有兴趣的旁友可以看看论文并且自行探索~
如果你喜欢我的这篇博客的话,请点个赞吧!~如果你喜欢我的风格并且想了解更多相关的内容,可以关注我~我会不定期更新有趣的图像与视觉方面的知识并加入个人的独特理解~
您的支持就是对我最大的肯定。