JS 数据结构(四)--二叉堆

前言

本文中将要介绍的是二叉堆,它是一种特殊的二叉树,也就是堆数据结构,也叫做二叉堆.它能快速高效地找出最大值和最小值,常被用于优先队列. (关于二叉树的相关文章之后会写)

定义

• 它是一棵完全二叉树,表示树的每一层都有左侧和右侧子节点(除了最后一层的叶节点),并且最后一层的叶节点尽可能都是左侧子节点,这叫做结构特性
• 二叉堆不是最小堆就是最大堆.最小堆允许你快速的导出树的最小值,最大值允许你快速导出树的最大值.所有的节点都大于等于(最大堆) 或小于等于(最小堆)每个它的子节点.这叫作堆特性

实现(最小堆)

主要方法

• insert (value): 向方法中插入一个新的值.如果插入成功,返回true,否则返回false
• extract(): 这个方法移除最小值(最小堆)或最大值(最大堆),并返回这个值
• findMinimum():这个方法返回最小值(最小堆)或最大值(最大堆)且不会移除这个值

获取节点 使用一个数组,通过索引值检索父节点,左侧和右侧节点的值.

• getLeftIndex(index): 获取它的左侧子节点位置, 操作逻辑 2 * index + 1
• getRightIndex(index): 获取它的右侧子节点位置, 操作逻辑 2 * index + 1
• getParentIndex(index) : 获取父节点位置,操作逻辑 index / 2

辅助方法

• size(): 获取长度
• isEmpty(): 判断是为空

const Compare = {
  LESS_THAN: -1,
  BIGGER_THAN: 1,
  EQUALS: 0
};

function defaultCompare(a, b) {
  if (a === b) {
    return Compare.EQUALS;
  }
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
function swap(array, a, b) {
  [array[a], array[b]] = [array[b], array[a]];
}


class MinHeap {
  constructor() {
    this.compareFn = defaultCompare;
    this.heap = [];
  }
  getLeftIndex(index) {
    return (2 * index) + 1;
  }
  getRightIndex(index) {
    return (2 * index) + 2;
  }
  getParentIndex(index) {
    if (index === 0) {
      return undefined;
    }
    return Math.floor((index - 1) / 2);
  }
  size() {
    return this.heap.length;
  }
  isEmpty() {
    return this.size() <= 0;
  }
  clear() {
    this.heap = [];
  }
  findMinimum() {
    return this.isEmpty() ? undefined : this.heap[0];
  }
  insert(value) {
    if (value != null) {
      const index = this.heap.length;
      this.heap.push(value);
      this.siftUp(index);
      return true;
    }
    return false;
  }
  siftDown(index) {
    let element = index;
    const left = this.getLeftIndex(index); //获取左侧子节点
    const right = this.getRightIndex(index); //获取右侧子节点
    const size = this.size(); 
    if (
      left < size &&
      this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN   
    ) {  
      element = left;  //交换元素
    }
    if (
      right < size &&
      this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
    ) {
      element = right; //交换元素
    }
    if (index !== element) {
      swap(this.heap, index, element); //交换位置
      this.siftDown(element);
    }
  }
  siftUp(index) {  //上移操作
    let parent = this.getParentIndex(index);
    while (
      index > 0 &&
      this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
    ) {
      swap(this.heap, parent, index);
      index = parent;
      parent = this.getParentIndex(index);
    }
  }
  extract() {
    if (this.isEmpty()) {
      return undefined;
    }
    if (this.size() === 1) {
      return this.heap.shift();
    }
    const removedValue = this.heap[0];
    this.heap[0] = this.heap.pop();
    this.siftDown(0);
    return removedValue;
  }

  getAsArray() {
    return this.heap;
  }
}



let heap = new MinHeap();

heap.insert(2);
heap.insert(3);
heap.insert(4);
heap.insert(5);

heap.insert(2);

console.log(heap.getAsArray());

console.log('Heap size: ', heap.size()); // 5
console.log('Heap is empty: ', heap.isEmpty()); // false
console.log('Heap min value: ', heap.findMinimum()); // 1

heap = new MinHeap();
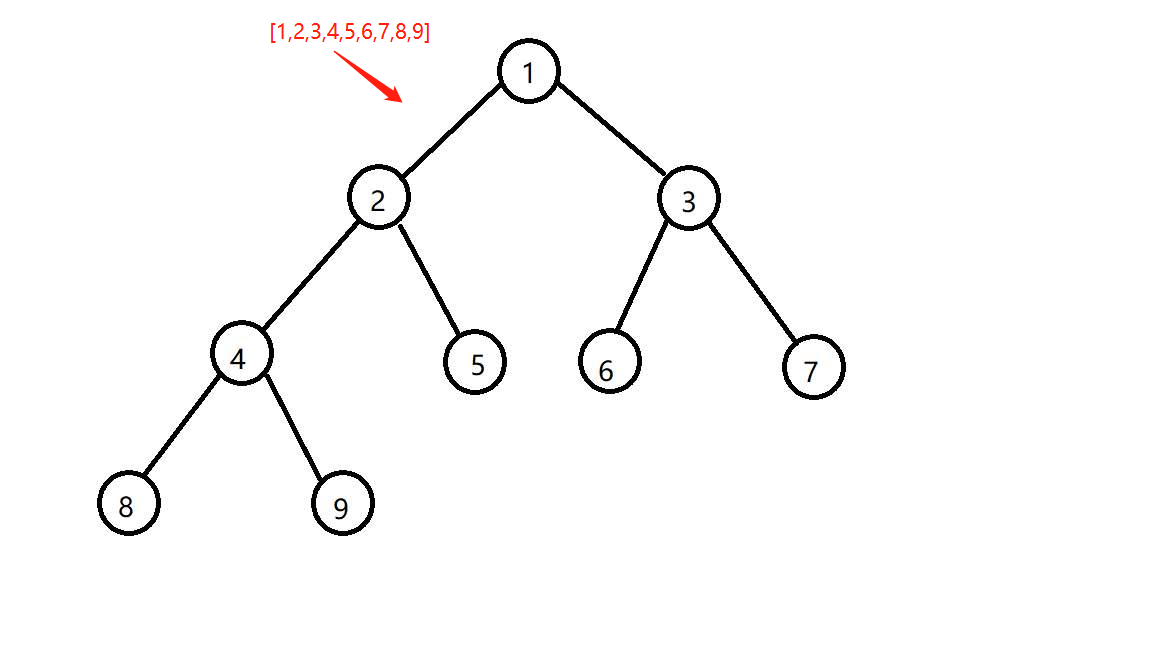
for (let i = 1; i < 10; i++) {
  heap.insert(i);
}

console.log(heap.getAsArray());

console.log('Extract minimum: ', heap.extract()); // 1
console.log(heap.getAsArray()); // [2, 4, 3, 8, 5, 6, 7, 9]

实现(最大堆)

MaxHeap 类的算法与MinHeap的算法一模一样.不同之处在于 我们要把所有的> (大于)的比较换成<(小于)的比较

function reverseCompare(compareFn){
  return (a,b)=> compareFn(b,a)
} 

class MaxHeap extends MinHeap{
  constructor(){
    super() 
    this.compareFn = reverseCompare(defaultCompare);
  }
}

const maxHeap = new MaxHeap();

maxHeap.insert(2);
maxHeap.insert(3);
maxHeap.insert(4);
maxHeap.insert(5);
maxHeap.insert(1);

console.log(maxHeap.getAsArray());

console.log('Heap size: ', maxHeap.size()); // 5
console.log('Heap is empty: ', maxHeap.isEmpty()); // false
console.log('Heap min value: ', maxHeap.findMinimum()); // 5

maxHeap.insert(6);
maxHeap.insert(9);
maxHeap.insert(10);
maxHeap.insert(14);
console.log(maxHeap.getAsArray()); // [14, 10, 6, 9, 1, 3, 5, 2, 4]
console.log('Extract minimum: ', maxHeap.extract()); // 14
console.log(maxHeap.getAsArray()); //   [10, 9, 6, 4, 1, 3, 5, 2]

结语

本次分享到这里了 与君共勉. 前端界的一枚小学生!!!