10- 网络上病毒传播的SIR模型 用Links建模网络动力学
首先,我们需要知道SIR模型是什么。


首先,我们需要知道SIR模型是什么。
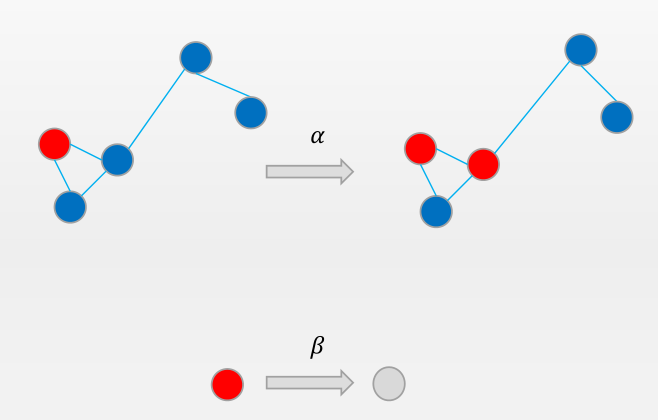
经典的SIR模型:
感染者有α 的概率感染健康者,
感染者有β的概率治疗成功,恢复之后就不会再被感染(neilogo的模型中是:痊愈后有一定的概率会获得病毒抗性)。

将人群分成三种状态:
S: 易感态、疑似态(Susceptibility)
I: 感染态(Infection)
R: 恢复态(Recovery)
三种状态彼此之间可以以一定的概率彼此之间相互转换
感染态可以沿着网络进行传播。
实现思路:
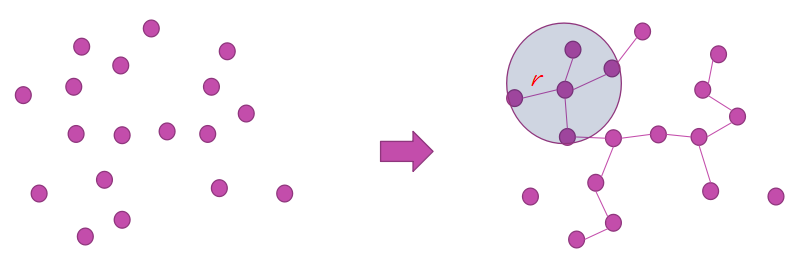
- 随机放置节点,遍历turtles,在半径r 内的节点都和该 turtle 相连;

- 使用 layout-spring 函数进行可视化;
- 患者有一定概率传染给健康者,患者在患病初期并不知道自己感染,患者有一定几率痊愈
- 患者痊愈后,有一定的概率会获得病毒抗性。对病毒产生抗性的患者无法被感染。
- 获得病毒抗性的人标记为灰色,并标记连边为灰色,记作无效节点
- 能选定初始的节点数、平均度、传播源点数
- 能指定传播速度、患者自检频率、痊愈比例、获得病毒抗性的比例
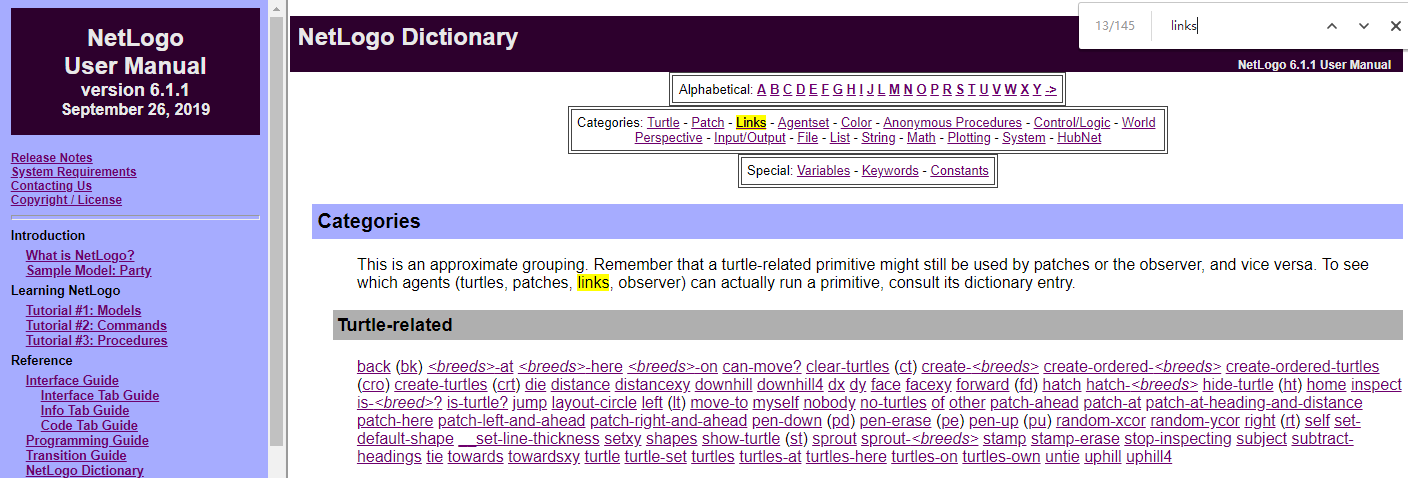
预备的代码知识:
Link对象
属性:
- end1,end2 属性
代表link两端的节点,end1代表起点,end2代表终点。
- link-neighbors 对象集合
ask turtle 0
[
create-links-with other turtles
ask link-neighbors [ set color red ] ;; turtles 1 and 2 turn red
]link有关的函数:
- create-links-from
用法:
create-links-from turtleset
创建其他 turtles 与 当前 turtle的连边(从其他 turtles指向当前 turtle)
- create-links-to
ask turtle 0 [ create-links-to other turtles ] 创建当前 turtle 到 其他 turtles的连边
- in-link-neighbors
指定已经和当前 turtle 创建连边的 邻居
- in-link-from
这是个回调函数,会返回两个turtle之间的连边(有向的,或者无向的都行)。如果有多条,就返回随机的一条边。如果没有,就显示nobody。
ask turtle 1 [ show in-link-from turtle 0 ] ;; shows link 0 1
ask turtle 0 [ show in-link-from turtle 1 ] ;; shows nobodyself与myself的区别
- self:指代当前语境中的对象
- myself:[ ] 的上一层的对象
layout-spring
- 一种将连边 视作弹簧的网络可视化方法。
- 将每个节点视作小球,连边视作弹簧,并且小球之间有斥力,弹簧之间有拉力。并使这些节点组成的系统处于受力平衡的状态。
用法:
layout-spring turtle-set link-set spring-constant spring-length repulsion-constant
五个变量的意思分别是:turtles集合对象、link 集合对象、弹簧系数(常量)、弹簧的自然长度、斥力系数(两个节点存在除了弹簧外的另一种斥力,这是1个单位距离处的2个节点将彼此施加的力。)
示例:
layout-spring turtles links 0.3 (world-width / (sqrt number-of-nodes)) 1

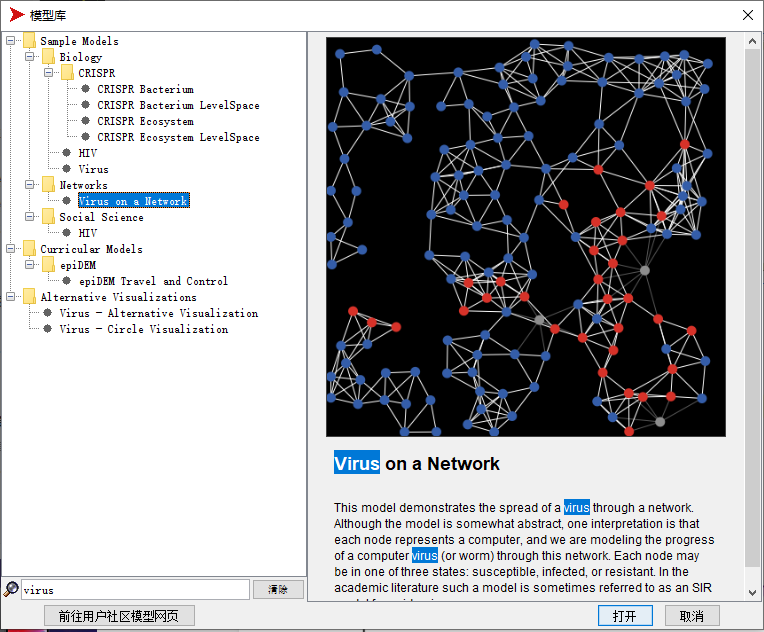
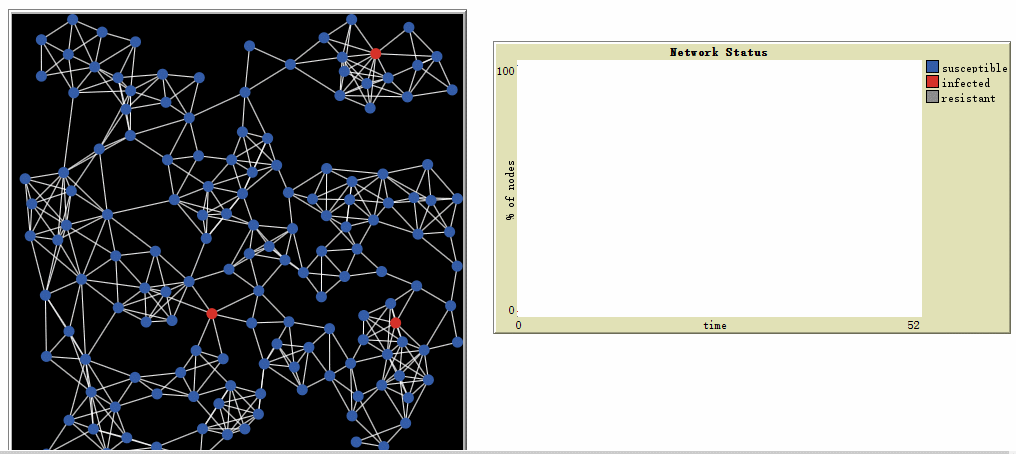
然后我们可以直接使用模型库中的 Virus on a Network

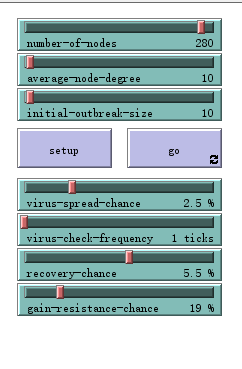
模型解读:
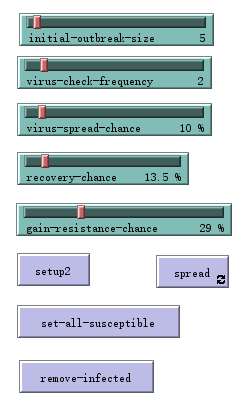
- number-of-nodes ------ 节点数量
- average-node-degree ------ 平均每个节点的度(与其他节点的连边数量)
- initial-outbreak-size ------- 初始的感染者个数
- VIRUS-SPREAD-CHANCE -------- α (感染者有α 的概率感染健康者)
- VIRUS-CHECK-FREQUENCY ------ 检查病毒的间隔时间
- RECOVERY-CHANCE ------- β (感染者有β的概率治疗成功)
- GAIN-RESISTANCE-CHANCE ------ 获得病毒抗性的概率

我调了多组参数进行了大量实验,观察到 :感染者的人数总会经历一个从逐渐增多,到逐渐下降的 “山形函数”。

这是 Uri Wilensky 在 2008 写的模型之一。

以下是我个人读懂这位老兄的模型代码后写的一些注解,供大家参考。
turtles-own
[
infected? ;; 布尔值,如果为真,则是被感染状态
resistant? ;; 如果为真,获得病毒抗性,无法被感染
virus-check-timer ;; 距离上一次治疗过去了多少时间步,大于virus-check-frequency的时候,此人会去接受治疗,于是置0。
;; 为0的时候,该个体会变成易感状态
]
to setup
clear-all
setup-nodes ;; 调用初始化节点 的函数
setup-spatially-clustered-network ;; 调用 初始化网络 的函数
ask n-of initial-outbreak-size turtles
[ become-infected ] ;; 初始化指定数量的感染者
ask links [ set color white ] ;; 初始化连边为白色
reset-ticks
end
to setup-nodes ;;初始化节点
set-default-shape turtles "circle"
create-turtles number-of-nodes
[
; 为了生成的节点不会分布在 视窗 的边缘
setxy (random-xcor * 0.95) (random-ycor * 0.95)
become-susceptible ;; 全部节点都是易感的
set virus-check-timer 0
]
end
to setup-spatially-clustered-network ;; 初始化网络
let num-links (average-node-degree * number-of-nodes) / 2 ;;新建一个全局变量:连边数
while [count links < num-links ]
[
ask one-of turtles
[
;; 选择 在不和该turtle为邻居的其他节点中,距离该turtle最近的节点,赋值给choice
let choice (min-one-of (other turtles with [not link-neighbor? myself])
[distance myself])
;; 只要存在符合的节点,就创建连边
if choice != nobody [ create-link-with choice ]
]
]
;; 这里用到layout-spring,就是那个把连边当作弹簧的可视化方法
repeat 10
[
layout-spring turtles links 0.3 (world-width / (sqrt number-of-nodes)) 1
]
end
to go
if all? turtles [not infected?] ;; 如果全部的状态为未被感染,那就停止运行
[ stop ]
ask turtles
[
set virus-check-timer virus-check-timer + 1 ;;每次go,都给 “距离上一次病毒检查过去了多少时间步” 记一次时
if virus-check-timer >= virus-check-frequency ;; 定期做检查
[ set virus-check-timer 0 ] ;; 置0
]
;;调用函数,实现感染者传播病毒
spread-virus
;; 调用函数,实现健康者定期做治疗
do-virus-checks
tick
end
to become-infected ;; 个体被感染
set infected? true
set resistant? false
set color red
end
to become-susceptible ;; 个体变成易感的
set infected? false
set resistant? false
set color blue
end
to become-resistant ;; 个体被获得病毒抗性
set infected? false
set resistant? true
set color gray
ask my-links [ set color gray - 2 ] ;; 让无效节点的连边颜色变灰
end
to spread-virus ;; 感染者传播病毒
ask turtles with [infected?]
[ ask link-neighbors with [not resistant?]
[ if random-float 100 < virus-spread-chance
[ become-infected ] ] ]
end
to do-virus-checks ;; 健康者定期做治疗
ask turtles with [infected? and virus-check-timer = 0]
[
if random 100 < recovery-chance ;; 有一定概率治愈
[
ifelse random 100 < gain-resistance-chance
[ become-resistant ] ;;在治愈的基础上,有一定概率能获得病毒抗性
[ become-susceptible ] ;;不够幸运,未能获得病毒抗性的人,重新变成易感的
]
]
end
; Copyright 2008 Uri Wilensky.
; See Info tab for full copyright and license.
后话:
大家如果遇到不会的函数,一定要多从词典中找相关的一些介绍。


模型的不足之处
- 未考虑长程的连边
然而交通网络的出现与发展让更多人能够跨距离地接触
- 未考虑连边异质性现象
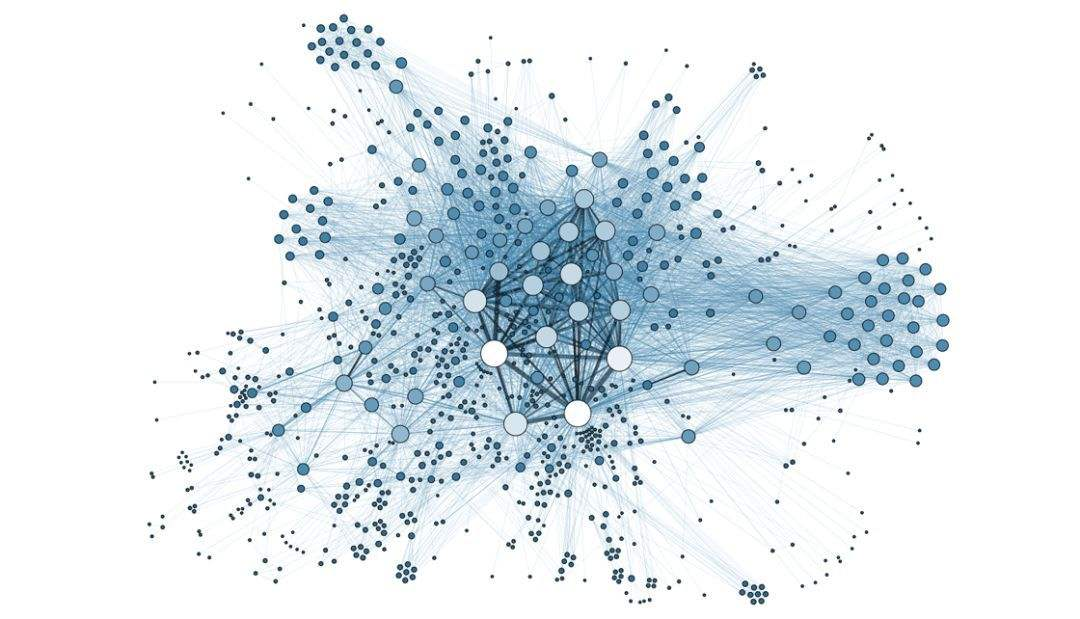
现实情况中,少数的节点拥有极其多的连接,而大多数节点只有很少量的连接。
改进:
将网络修改成 无标度网络
可以尝试引入 Preferential Attachment 模型的一些代码。

--------------------------------------
今天闲着没事,就来整合一下模型库中的Preferential Attachment 模型和 之前学的病毒传播模型,以实现 无标度网络下的病毒传播模型。
模型库中的Preferential Attachment 模型已经能很好得实现无标度模型生成了,所以我简单地整合一下代码就行。

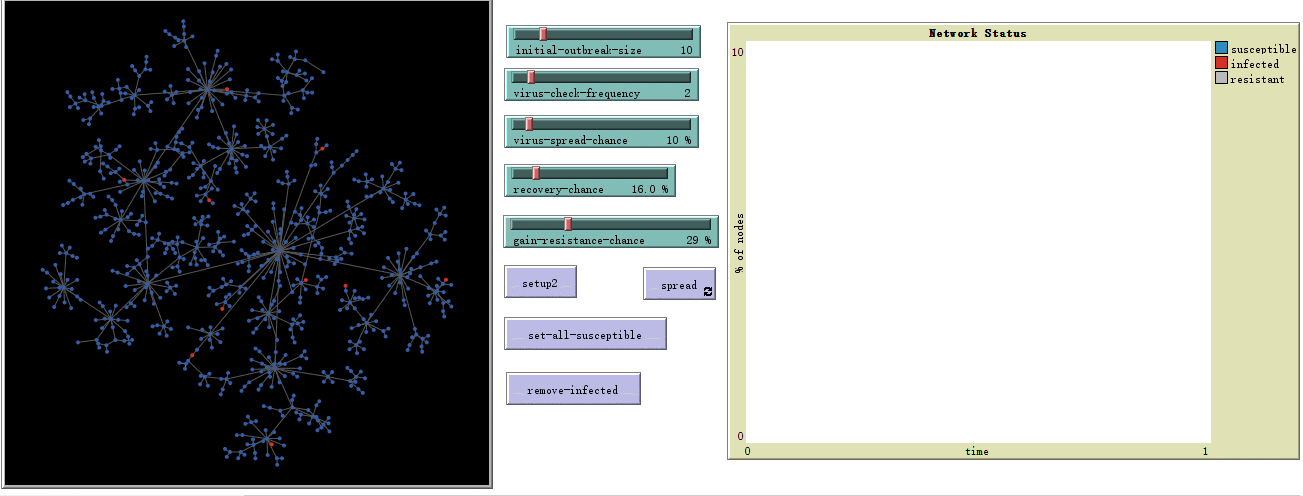
- 新加的滑块和之前的一样,只不过多了 set-all-susceptible 和 remove-infected
前者是为了实验第二波病毒传播会是怎样的情形,
后者是为了清除所有初始感染者,方便重新设置。

- 绘图方面和之前不变

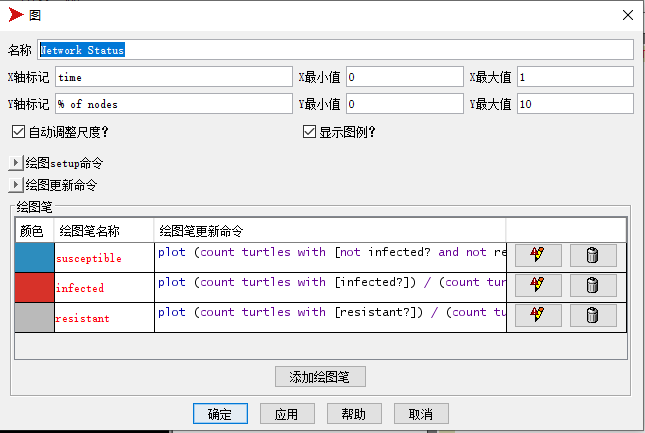
Network Status
横轴: time
纵轴 : % of nodes
- susceptible
plot (count turtles with [not infected? and not resistant?]) / (count turtles) * 100
- infected
plot (count turtles with [infected?]) / (count turtles) * 100
- resistant
plot (count turtles with [resistant?]) / (count turtles) * 100
整合的时候有几个要留意的地方:
- setup2 不用调用初始化节点和网络,也不用layout-spring函数
- setup2 要删掉 “ clear-all ”
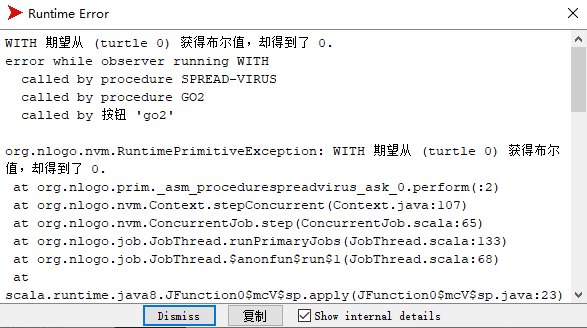
- setup2 要给变量 infected? 和 resistant? 初始化为布尔值。
ask turtles [
set infected? false
set resistant? false
]不然会报错。因为默认初始化的方法是让这个变量为0。

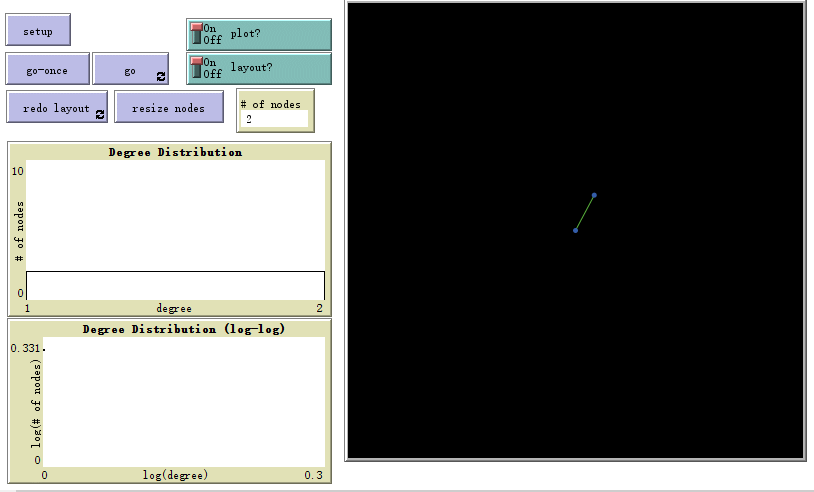
模型运行界面:

附件在这,想探索的同学自行下来玩玩: