
LFU算法及其优化策略——算法篇
前不久写了LRU算法系列文章,今天来介绍一下和LRU算法并驾齐驱的另一个算法——LFU。
LFU全称是最不经常使用算法(Least Frequently Used),LFU算法的基本思想和所有的缓存算法一样,都是基于locality假设(局部性原理):
如果一个信息项正在被访问,那么在近期它很可能还会被再次访问。
LFU是基于这种思想进行设计:一定时期内被访问次数最少的页,在将来被访问到的几率也是最小的。
相比于LRU(Least Recently Use)算法,LFU更加注重于使用的频率。
原理
LFU将数据和数据的访问频次保存在一个容量有限的容器中,当访问一个数据时:
- 该数据在容器中,则将该数据的访问频次加1。
- 该数据不在容器中,则将该数据加入到容器中,且访问频次为1。
当数据量达到容器的限制后,会剔除掉访问频次最低的数据。下图是一个简易的LFU算法示意图。
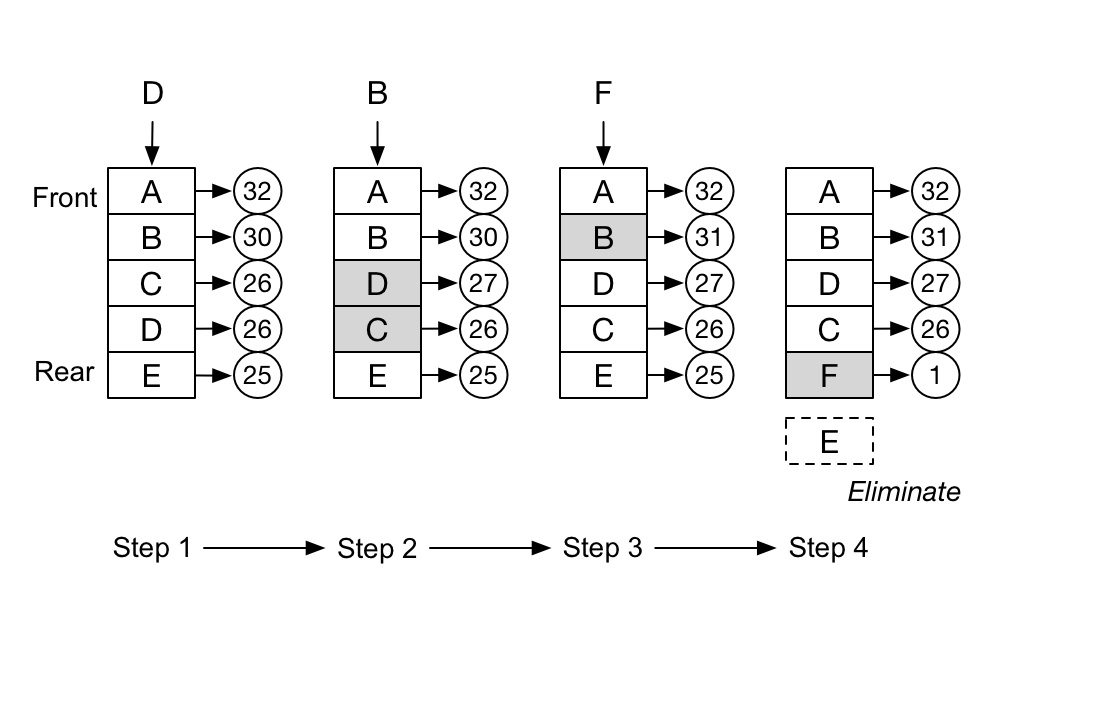
上图中的LRU容器是一个链表,会动态地根据访问频次调整数据在链表中的位置,方便进行数据的淘汰,可以看到,在第四步时,因为需要插入数据F,而淘汰了数据E。
LFU实现
LFU的实现一共有三种方案,但是思想都是一样的,下面我们先来看最简单的一种实现。
基于双端链表+哈希表
public class LFUCache {
private Node head; // 头结点 简化null判断
private Node tail; // 尾结点 简化null判断
private int capacity; // 容量限制
private int size; // 当前数据个数
private Map<Integer, Node> map; // key和数据的映射
public LFUCache(int capacity) {
this.capacity = capacity;
this.size = 0;
this.head = new Node(0, 0, 0);
this.tail = new Node(0, 0, 0);
this.head.next = tail;
this.tail.pre = head;
this.map = new HashMap<>();
}
public int get(int key) {
// 从哈希表中判断数据是否存在
Node node = map.get(key);
if (node == null) {
return -1;
}
// 如果存在则增加该数据的访问频次
freqPlus(node);
return node.value;
}
public void put(int key, int value) {
if (capacity <= 0) {
return;
}
Node node = map.get(key);
if (node != null) {
// 如果存在则增加该数据的访问频次
node.value = value;
freqPlus(node);
} else {
// 淘汰数据
eliminate();
Node newNode = new Node(key, value, 0);
map.put(key, newNode);
size++;
// 将新数据插入到末尾
Node tailPre = tail.pre;
tail.pre = newNode;
newNode.pre = tailPre;
newNode.next = tail;
tailPre.next = newNode;
// 增加访问频次
freqPlus(newNode);
}
}
private void freqPlus(Node node) {
node.frequency++;
Node temp = node.pre;
int freq = node.frequency;
while(temp != null) {
// 使用大于号的原因是将最后访问的数据排在旧数据之前
if (temp.frequency > freq || temp == head) {
node.pre.next = node.next;
node.next.pre = node.pre;
// 根据访问频次排序调整位置
Node tempNext = temp.next;
temp.next = node;
tempNext.pre = node;
node.next = tempNext;
node.pre = temp;
break;
}
temp = temp.pre;
}
}
private void eliminate() {
if (size < capacity) {
return;
}
// 从尾结点的pre节点之间删除即可
Node last = tail.pre;
last.pre.next = tail;
tail.pre = last.pre;
map.remove(last.key);
size--;
last = null;
}
}
class Node {
int key;
int value;
int frequency;
Node pre;
Node next;
Node(int key, int value, int frequency) {
this.key = key;
this.value = value;
this.frequency = frequency;
}
}
整个逻辑还是比较清晰的,注意小心的操纵pre(前置节点)、next(后置节点)这两个指针即可,同时注意通过freqPlus()方法保证链表中的数据是按照访问频次排序的。
也正是因为freqPlus这个方法,导致put()和get()操作的时间复杂度都为O(N)。
基于双哈希表实现
为了进一步降低上一种方案的时间复杂度,我们可以通过双哈希表来实现。
class LFUCache {
private int capacity; // 容量限制
private int size; // 当前数据个数
private int minFreq; // 当前最小频率
private Map<Integer, Node> map; // key和数据的映射
private Map<Integer, LinkedHashSet<Node>> freqMap; // 数据频率和对应数据组成的链表
public LFUCache(int capacity) {
this.capacity = capacity;
this.size = 0;
this.minFreq = 1;
this.map = new HashMap<>();
this.freqMap = new HashMap<>();
}
public int get(int key) {
Node node = map.get(key);
if (node == null) {
return -1;
}
// 增加数据的访问频率
freqPlus(node);
return node.value;
}
public void put(int key, int value) {
if (capacity <= 0) {
return;
}
Node node = map.get(key);
if (node != null) {
// 如果存在则增加该数据的访问频次
node.value = value;
freqPlus(node);
} else {
// 淘汰数据
eliminate();
// 新增数据并放到数据频率为1的数据链表中
Node newNode = new Node(key, value);
map.put(key, newNode);
LinkedHashSet<Node> set = freqMap.get(1);
if (set == null) {
set = new LinkedHashSet<>();
freqMap.put(1, set);
}
set.add(newNode);
minFreq = 1;
size++;
}
}
private void eliminate() {
if (size < capacity) {
return;
}
LinkedHashSet<Node> set = freqMap.get(minFreq);
Node node = set.iterator().next();
set.remove(node);
map.remove(node.key);
size--;
}
void freqPlus(Node node) {
int frequency = node.frequency;
LinkedHashSet<Node> oldSet = freqMap.get(frequency);
oldSet.remove(node);
// 更新最小数据频率
if (minFreq == frequency && oldSet.isEmpty()) {
minFreq++;
}
frequency++;
node.frequency++;
LinkedHashSet<Node> set = freqMap.get(frequency);
if (set == null) {
set = new LinkedHashSet<>();
freqMap.put(frequency, set);
}
set.add(node);
}
}
class Node {
int key;
int value;
int frequency = 1;
Node(int key, int value) {
this.key = key;
this.value = value;
}
}
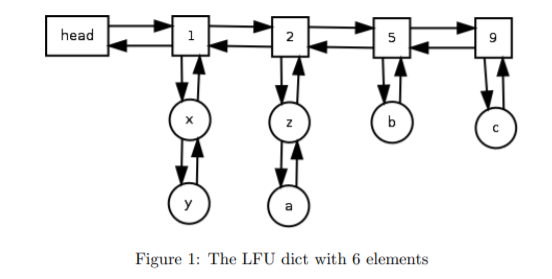
基于JDK的LinkedHashSet这个类来模拟链表,我们可以将put()和get()操作的时间复杂度降低到O(1)级别。这套方案的实现来自于这篇论文《An O(1) algorithm for implementing the LFU cache eviction scheme》,下面是该论文中的一个示意图,可以辅助理解。
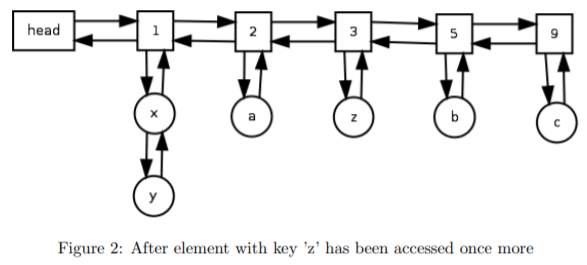
LFU相比于LRU的优劣
区别:
LFU是基于访问频次的模式,而LRU是基于访问时间的模式。
优势:
在数据访问符合正态分布时,相比于LRU算法,LFU算法的缓存命中率会高一些。
劣势:
- LFU的复杂度要比LRU更高一些。
- 需要维护数据的访问频次,每次访问都需要更新。
- 早期的数据相比于后期的数据更容易被缓存下来,导致后期的数据很难被缓存。
- 新加入缓存的数据很容易被剔除,像是缓存的末端发生“抖动”。
LFU算法优化
从上面的优劣分析中我们可以发现,优化LFU算法可以从下面几点入手:
- 更加紧凑的数据结构,避免维护访问频次的高消耗。
- 避免早期的热点数据一直占据缓存,即LFU算法也需有一些访问时间模式的特性。
- 消除缓存末端的抖动。
具体的优化方案我会在之后的文章中结合具体实例进行介绍。
总结
本文介绍了基本的LFU算法,以及它的O(N)级别和O(1)级别的具体实现。后面进行了LRU算法和LFU算法的优劣分析,并得出了LFU算法的优化方向。