夜黑风高的某个晚上,脑子突然卡壳了,一下子想不明白,做01背包内循环的循环变量递减,而当01背包变成完全背包时,把内循环的循环变量改成递增就ok了。这究竟是为什么?想不明白。于是乎有了下文,认真思考总结一下。背包问题属于动态规划的经典题型。
引例
有一个容量Q的背包,有N件物品,第i件物品重weight[i]、价值为value[i],求该背包所能装下的最大价值。
可抽象为这种模型的问题称为背包问题。背包问题可以有很多变种,本篇只讨论01背包和完全背包。
下面举一个不太生动的例子。
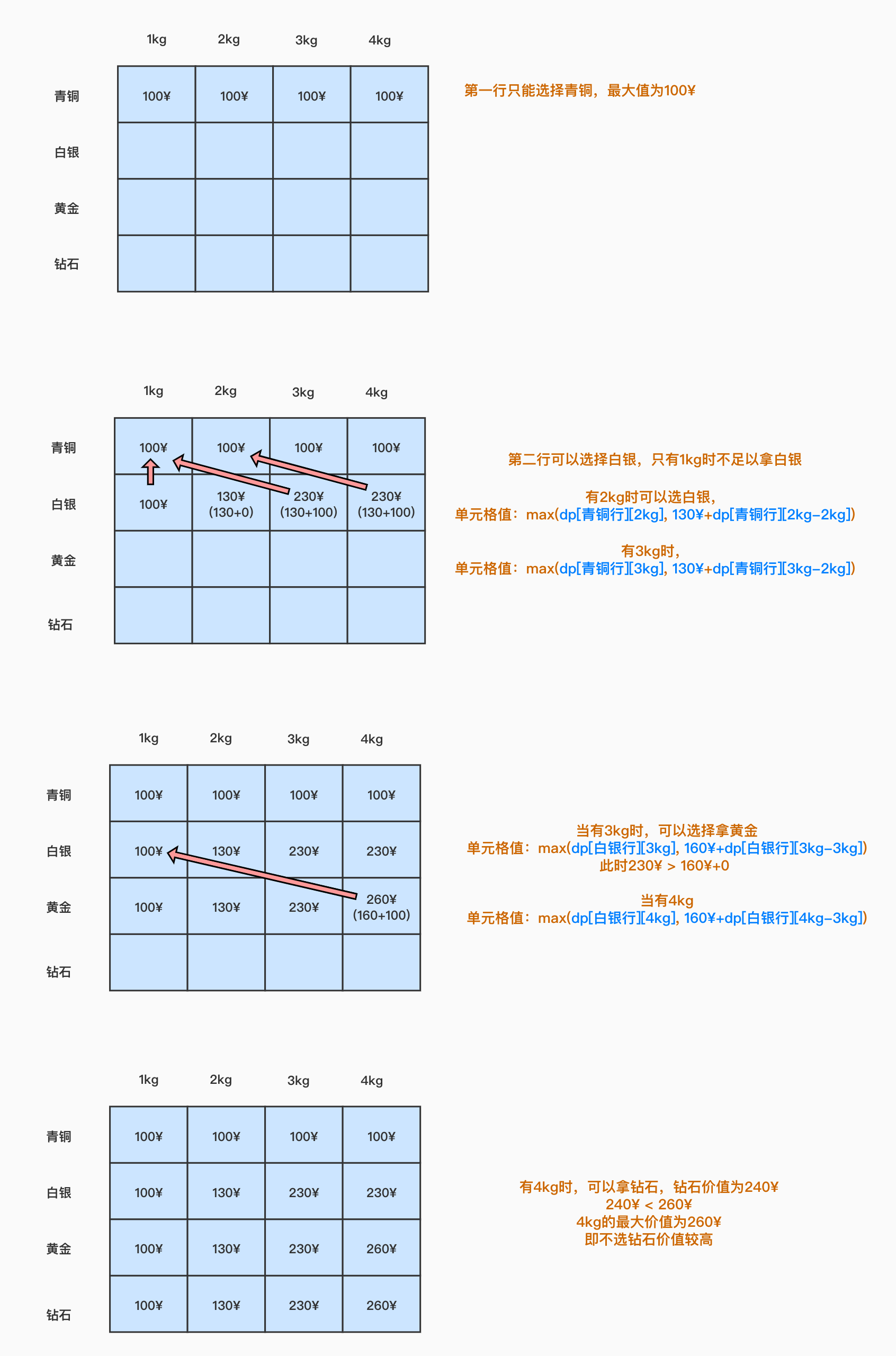
有四块石头,青铜、白银、黄金,钻石,重分别为1kg,2kg,3kg,4kg,价值分别为¥100,¥130,¥160,¥240,此时你有一个最大负重4kg的背包,求背包能装下的最大价值。
如果直接采用贪心,稍微目测一下就知道结果是错的。那么这道题我们如何使用dp来解决呢?
01背包
为什么称为01背包,因为对于每一个item来说,它只可能有2种状态,要么选它要么不选它。如果此时采用递归或许更好理解一些,但本篇不进行展开。
我们可以用一个二维数组来表示最大价值,习惯性的,我们把它命名为dp,用dp[i][j]来表示,可选范围为前i个,背包最大容量j,所能获得的最大价值。
撇开其他的不管。算法在执行到某个i,j时,思考一下此时最大值即dp[i][j]该如何表示?
如果j > weight[i]即可以选择第i项,如果选择了第i项,剩余的容量就剩下j-weight[i],在剩余的容量里取前第i-1项的最大价值加上第i项的价值,即可表示选择了第i项的最大价值。之后,在 选择第i项的最大价值 与 不选第i项的最大价值,取较大者即为dp[i][j]。用代码来表示如下
if j > weight {
dp[i][j] = max(dp[i-1][j], value + dp[i-1][j-weight])
} else {
// 如果j比weight[i]小,即第i项并不可选,直接为前i-1项,容量j能取得最大价值即可
dp[i][j] = dp[i-1][j]
}
动态规划的目的在于寻找最优解,关键在于利用重复子问题(或者说是局部最优解)。在上述中dp[i-1][j-weight[i]])就是重复子问题。
方程dp[i][j] = max(dp[i-1][j], value[i] + dp[i-1][j-weight[i]])为状态转移方程。
基于上述问题我们可以写出常规01背包的解题模版
func maxProfit(cap int, w []int, v []int) int {
n := len(w)
// 多申请一个行可省去越界判断
dp := make([][]int, n+1)
for i := 0; i <= n; i++ {
dp[i] = make([]int, cap+1)
}
for i := 1; i <= n; i++ {
value := v[i-1]
weight := w[i-1]
for j := 1; j <= cap; j++ {
if j >= weight {
dp[i][j] = max(dp[i-1][j], value+dp[i-1][j-weight])
} else {
dp[i][j] = dp[i-1][j]
}
}
}
return dp[n][cap]
}
空间优化方法
稍微细心一点就会发现,观察状态转移方程或上述表格,新一行的状态(单元格的值)只与他上一行有关,而不必关心其他的行。比如在确定黄金行的状态时,我们只需要看白银行,而无需理会青铜行的状态。
基于以上理解,我们完全可以只用一维的空间dp[j] j的范围为0~最大容量来表示状态。将原本需要O(nm)的空间优化成O(m)。
观察上文的图或者状态转移方程
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight])
在确定新的dp[j]时,我们需要旧的dp[j]或者dp[j]前面的状态(即dp[j-weight]),所以当我们只用一维空间来表示状态时,需要从后往前循环。
经过优化的模版
func maxProfit(cap int, w []int, v []int) int {
n := len(w)
dp := make([]int, cap+1)
for i := 1; i <= n; i++ {
value := v[i-1]
weight := w[i-1]
// 从后往前
for j := cap; j >= 0; j-- {
if j >= weight {
dp[j] = max(dp[j], value+dp[j-weight])
}
}
}
return dp[cap]
}
完全背包
当背包问题中每一种物品的数量从一个变为无限个时,01背包就变成完全背包。
现在你已经会做01背包了。稍微停下思考,当上述例子青铜白银黄金钻石的数量都变为无数个的时候该如何求解。
下面先用二维的数组来表示状态。
如上述例子,确定青铜行的状态时,青铜为1kg,当有2kg的背包,选了青铜后,还可以选青铜。
dp[青铜行][2kg] = 100¥ + dp[青铜行][2kg-1kg]
即状态转移如下
if j > weight {
dp[i][j] = max(dp[i-1][j], value + dp[i][j-weight])
} else {
dp[i][j] = dp[i-1][j]
}
以此我们可以写出完全背包的模版
func maxProfit(cap int, w []int, v []int) int {
n := len(w)
dp := make([][]int, n+1)
for i := 0; i <= n; i++ {
dp[i] = make([]int, cap+1)
}
for i := 1; i <= n; i++ {
value := v[i-1]
weight := w[i-1]
for j := 1; j <= cap; j++ {
if j >= weight {
dp[i][j] = max(dp[i-1][j], value+dp[i][j-weight])
} else {
dp[i][j] = dp[i-1][j]
}
}
}
return dp[n][cap]
}
观察状态转移方程,我们同样可以对完全背包进行空间优化。在确定新的dp[j]时,我们需要旧的dp[j]或者j前面新的状态(即dp[j-weight]),所以当我们只用一维空间来表示状态时,需要从前往后循环。
优化过后的模版
func maxProfit(cap int, w []int, v []int) int {
n := len(w)
dp := make([]int, cap+1)
for i := 1; i <= n; i++ {
value := v[i-1]
weight := w[i-1]
for j := 1; j <= cap; j++ {
if j >= weight {
dp[j] = max(dp[j], value+dp[j-weight])
}
}
}
return dp[cap]
}
LeetCode实践
494.目标和
来源:力扣(LeetCode) 链接:leetcode-cn.com/problems/ta…
这道题可以抽象为01背包问题。题目可这么解读,选择一部分数字添加+号,另一部分部分数字添加-号,两部分数字的绝对值只和相差S。换个角度,我们只要计算凑成(sum+S)/2的方法个数即可。每个数字最多只能选择一次。
func findTargetSumWays(nums []int, S int) int {
sum := 0
for _, v := range nums {
sum += v
}
if (sum + S) % 2 != 0 || S > sum {
return 0
}
w := (sum+S)/2
dp := make([]int, w+1)
dp[0] = 1
for _, num := range nums {
for j := w; j >= num; j-- {
dp[j] = dp[j] + dp[j-num]
}
}
return dp[w]
}
322.零钱兑换
来源:力扣(LeetCode) 链接:leetcode-cn.com/problems/co…
这道题可以抽象为完全背包问题。其中最大容量为总金额amount,不同面额的硬币为不同的物品,价值抽象为硬币的个数,这题比较特殊,物品的价值都为1。目标是求凑成amount的最少硬币个数。因为不同面额的硬币有若干个,所以该题属于完全背包问题。
func coinChange(coins []int, amount int) int {
if amount == 0 {
return 0
}
dp := make([]int, amount+1)
// 初始化为无穷大
for i := 0; i <= amount; i++ {
dp[i] = math.MaxInt32
}
for _, coin := range coins {
if coin <= amount {
// 硬币面额 == 目标数量 数量为1(最少)
dp[coin] = 1
}
for j := 1; j <= amount; j++ {
if j >= coin {
dp[j] = min(dp[j], 1 + dp[j-coin])
}
}
}
// 无法凑成
if dp[amount] == math.MaxInt32 {
return -1
}
return dp[amount]
}
小结
本文算是自己的总结,也可以当作背包问题的入门。回到那个夜黑风高的晚上,如果单纯看解题模版是肯定想不明白,为什么当01背包变成完全背包时,把内循环的循环变量改成递增就好了。但如果知道了如何进行空间优化,一切就十分好理解了。
背包问题虽然属于动态规划,但请不要在动态规划的题强行套用背包的解法。有时候即便能把各项抽像成背包问题,在处理容量这个元素时,是每次加一(或减一)进行枚举的,这意味当容量非常大时,那么要么申请空间时溢出,要么结果超时。背包问题还有很多变种,推荐阅读文末的背包九讲。