Leetcode刷题之数学如果 x 整除 y（y mod x == 0），则对于所有 i，mi <= ni。 x 和 y

分解数

首先我们需要了解，任何一个数都可以分解成素数的乘积，例如 84 = $2^2$ * $3^1$ * $5^0$ * $7^1$ * $11^0$ * $13^0$ * $17^0$ * …

整除

令 x = $2^{m0}$ * $3^{m1}$ * $5^{m2}$ * $7^{m3}$ * $11^{m4}$ * …
令 y = $2^{n0}$ * $3^{n1}$ * $5^{n2}$ * $7^{n3}$ * $11^{n4}$ * …

如果 x 整除 y（y mod x == 0），则对于所有 i，mi <= ni。

最大公约数最小公倍数

x 和 y 的最大公约数为：gcd(x,y) = $2^{min(m0,n0)}$ * $3^{min(m1,n1)}$ * $5^{min(m2,n2)}$ * ...

x 和 y 的最小公倍数为：lcm(x,y) = $2^{max(m0,n0)}$ * $3^{max(m1,n1)}$ * $5^{max(m2,n2)}$ * ...

204. 计数质数(Easy)

统计所有小于非负整数 n 的质数的数量。

示例:

输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

解法一：能想到的最简单的办法就是遍历小于n的所有数，一个一个判断是否为质数，但是这种时间复杂度太高

class Solution {
    public int CountPrimes(int n) {
        int count = 0;
        for (int i = 2; i < n; i++)
        {
            boolean sign = true;
            //判断i是否为质数
            for (int j = 2; j < i; j++)
            {
                if (i % j == 0)
                {
                    sign = false;
                    break;
                }
            }
            //如果是，就+1
            if (sign)
                count++; ;
        }
        return count;
    }
}

解法二：对上述暴力递归算法进行优化，其实判断只需要到sqrt(n)即可，为什么呢，我们看个例子，比如n=8。

8 = 2 * 4
8 = sqrt(n) * sqrt(n)
8 = 4 * 2

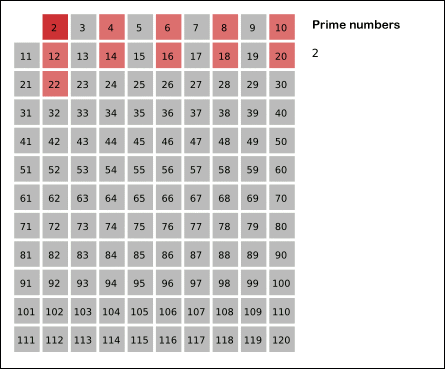
我们可以观察到，后面的那个乘积是前面的反过来的，所以我们遍历的时候只需要到sqrt(n)即可，并且，如果一个数是质数，那么其倍数就不为质数，如果一个数不为质数，当然其倍数也不为质数，所以我们可以准备一个boolean数组来辅助判断。借用一张labuladong大佬的图

class Solution {
    public int CountPrimes(int n){
        //准备一个数组，并初始化为true
        boolean[] isPrim = new boolean[n];
        Arrays.fill(isPrim, true);
        
        //将为质数的倍数都置为false
        for (int i = 2; i < n; i++) {
            if (isPrim[i]){
                //i的倍数都不为质数
                for (int j = 2 * i; j < n; j++) {
                    isPrim[j] = false;
                }
            }
        }
        
        //统计质数的个数
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (isPrim[i]){
                count++;
            }
        }
        return count;
    }
}

求最大公约数

辗转相除法，又名欧几里德算法。具体的步骤就是：用较小数除较大数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是0为止。

举个例子就是：比如两个数字，x = 453，y = 36；
453 % 36 = 21；
36 % 21 = 15；
21 % 15 = 6；
15 % 6 = 3；
6 % 3 = 0；
最后得出最大公约数为3

int GCD(int x,int y){
    //求出余数
    int r = x % y;
    while(r != 0){
        x = y;
        y = r;
        //用出现的余数 除以 上个式子较小的数
        r = x % y;
    }
    return y;
}

最小公倍数为两数的乘积除以最大公约数。
int lcm(int a, int b) {
    return a * b / GCD(a, b);
}

方法二：Stein算法

对于 a 和 b 的最大公约数 f(a, b)，有：

如果 a 和 b 均为偶数，f(a, b) = 2*f(a/2, b/2);
如果 a 是偶数 b 是奇数，f(a, b) = f(a/2, b);
如果 b 是偶数 a 是奇数，f(a, b) = f(a, b/2);
如果 a 和 b 均为奇数，f(a, b) = f(b, a-b);

乘 2 和除 2 都可以转换为移位操作。

public int gcd(int a, int b) {
    if (a < b) {
        return gcd(b, a);
    }
    if (b == 0) {
        return a;
    }
    
    //判断是奇数还是偶数
    boolean isAEven = isEven(a), isBEven = isEven(b);
    if (isAEven && isBEven) {
        return 2 * gcd(a >> 1, b >> 1);
    } else if (isAEven && !isBEven) {
        return gcd(a >> 1, b);
    } else if (!isAEven && isBEven) {
        return gcd(a, b >> 1);
    } else {
        return gcd(b, a - b);
    }
}

进制转换

504. 七进制数（Easy）

给定一个整数，将其转化为7进制，并以字符串形式输出。

示例 1:

输入: 100
输出: "202"

示例 2:

输入: -7
输出: "-10"
注意: 输入范围是 [-1e7, 1e7] 。

题解：题意是给定一个十进制数num，然后转换成七进制数，这个时候可以联想到“进制转换”的内容，转换成“七进制”，就用num不断地对7取余，然后再将这些余数加起来，最后反转

class Solution {
    public String convertToBase7(int num) {
        if (num == 0){
            return "0";
        }

        StringBuilder sb = new StringBuilder();
        boolean isNegative = num < 0;
        if (isNegative){
            num = -num;
        }

        while (num > 0){
            //收集余数，用商继续取余
            sb.append(num % 7);
            num = num / 7;
        }
        
        String ret = sb.reverse().toString();
        return isNegative ? "-" + ret : ret;
    }
}

405. 数字转换为十六进制数（Easy）

给定一个整数，编写一个算法将这个数转换为十六进制数。对于负整数，我们通常使用补码运算方法。

注意:

十六进制中所有字母(a-f)都必须是小写。
十六进制字符串中不能包含多余的前导零。如果要转化的数为0，那么以单个字符'0'来表示；对于其他情况，十六进制字符串中的第一个字符将不会是0字符。
给定的数确保在32位有符号整数范围内。
不能使用任何由库提供的将数字直接转换或格式化为十六进制的方法。

示例 1：

输入:
26
输出:
"1a"

示例 2：

输入:
-1
输出:
"ffffffff"

计算机中数字是以补码的形式存在的
负数->补码：首先要将原码->反码，即符号位不变，其余位置取反；然后反码->补码，在反码基础上+1。

题解：题目给出一个数，让我们转换成16进制，所以我们采取位操作的思路，每次取出最右边四位，

class Solution {
    public String toHex(int num) {
        if (num == 0){
            return "0";
        }
        //准备一个数组表示16进制对应的数
        char[] map = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f'};

        StringBuilder sb = new StringBuilder();
        //每次取4位进行转换
        while (num != 0){
            sb.append(map[num & 0b1111]);
            num >>>= 4;
        }
        //反转
        return sb.reverse().toString();
    }
}

168. Excel表列名称（Easy）

给定一个正整数，返回它在 Excel 表中相对应的列名称。

例如

    1 -> A
    2 -> B
    3 -> C
    ...
    26 -> Z
    27 -> AA
    28 -> AB 
    ...

示例 1:

输入: 1
输出: "A"

示例 2:

输入: 28
输出: "AB"

示例 3:

输入: 701
输出: "ZY"

题解：这道题和“七进制”那道题相似，只是这道题是从1开始，七进制那道题是从“0”开始。

输入的数是从1开始，对应A，最大的26对应Z。
正常的情况是0~25对应A~Z，所以我们可以将给定的n先减1，然后再对26取余，就可以解决

class Solution {
    public String convertToTitle(int n) {
        if (n == 0) {
            return "";
        }
        StringBuilder res = new StringBuilder();
        while (n > 0) {
            //刁钻的地方：n对26取余之后的值在--n之后才是正常的情况
            //对n取余：相当于把n分成26的倍数分，最小的那一份才是余数，只需要处理好这一份就可以
            res.append((char)(--n % 26 + 'A'));
            n /= 26;
        }
        return res.reverse().toString();
    }

    //未优化的方法
    public String convertToTitle(int n) {
        StringBuilder res = new StringBuilder();
        while (n > 0) {
            //当得到的是26时，特殊处理
            if (n % 26 == 0) {
                res.append('Z');
                n -= 26;
            } else {
                res.append(n % 26 - 1 + 'A');
                n -= n % 26;
            }
            n /= 26;
        }
        return res.toString();
    }
}

阶乘问题

172. 阶乘后的零（Easy）

给定一个整数 n，返回 n! 结果尾数中零的数量。

示例 1:

输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。

示例 2:

输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。

题解：

“0”是由2和5相乘得来的，比如10=2*5，100=2*2*5*5，每一对2*5就有1个0，而5的数量明显比2多，所以我们只需分析阶乘的因数中5的数量即可
要注意像25这种不只有一个5的要考虑清楚，所以只需要判断每个累乘的数有多少个 5 的因子即可，但是这种肯定会超时，所以需要优化
优化：由分析可得，每隔 5 个数，出现一个 5，每隔 25 个数，出现 2 个 5，每隔 125 个数，出现 3 个 5... 以此类推。最终 5 的个数就是 n / 5 + n / 25 + n / 125 ...

class Solution {
    public int trailingZeroes(int n) {
        int res = 0;
        while (n > 0){
            res += n / 5;
            n /= 5;
        }
        return res;
    }
}

字符串加法减法

67. 二进制求和（Easy）

给定两个二进制字符串，返回他们的和（用二进制表示）。输入为非空字符串且只包含数字 1 和 0。

示例 1:

输入: a = "11", b = "1"
输出: "100"

示例 2:

输入: a = "1010", b = "1011"
输出: "10101"

题解：这道题和大数相加的题目很类似，都是用字符串做加法运算，不同的只是这道题是“二进制”，做加法无非是对每一位做 数a和数b当前位的和 + 进位 运算，倒序相加，最后再倒回去即可。

class Solution {
    public String addBinary(String a, String b) {
        if (a == null || a.equals("0")){
            return b;
        }
        if (b == null || b.equals("0")){
            return a;
        }

        int i = a.length() - 1;
        int j = b.length() - 1;
        //进位
        int carry = 0;
        //用StringBuilder来拼接和
        StringBuilder str = new StringBuilder();

        //当a或b还未加完，或者还有进位的时候，就继续加，因为可能出现1+1=10这种情况
        while (carry == 1 || i >= 0 || j >= 0){
            //如果a/b当前位为1
            if (i >= 0 && a.charAt(i--) == '1'){
                carry++;
            }
            if (j >= 0 && b.charAt(j--) == '1'){
                carry++;
            }
            //如果carry < 2，说明没有进位，直接加
            //如果carry > 2，有进位，取余之后加
            str.append(carry % 2);
            carry /= 2;
        }
        //从低位加到高位的，但是写的时候是从高到低，所以需要反转
        return str.reverse().toString();
    }
}

415. 字符串相加（Easy）

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和。

注意：

num1 和num2 的长度都小于 5100.
num1 和num2 都只包含数字 0-9.
num1 和num2 都不包含任何前导零。
你不能使用任何內建 BigInteger 库，也不能直接将输入的字符串转换为整数形式。

题解：这道题和上道题很相似，上道题提到的“大数相加”就是这道题，题目给的数是非负整数的字符串形式，让我们将其相加，一样可以参考上道题的方法解答

例如：12 + 21
1. 从后计算，先是个位，1 + 2，初始进位为0，所以2 + 1 + 0 = 3，3 < 10，所以个位为3，carry为0
2. 接着是十位，1 + 2 + 0 = 3，carry同样是0，所以十位为3
3. 最后两个数的长度都已经用完了，而且进位也等于0，计算结束


class Solution {
    public String addStrings(String num1, String num2) {
        StringBuilder str = new StringBuilder();
        //进位
        int carry = 0;
        int i = num1.length() - 1;
        int j = num2.length() - 1;
        //还有进位，或者两数没加完
        while (carry == 1 || i >= 0 || j >= 0){
            //如果加完了就取0，否则取当前位的数
            int x = i < 0 ? 0 : num1.charAt(i--) - '0';
            int y = j < 0 ? 0 : num2.charAt(j--) - '0';
            //和num的当前位的数是由num1和num2及进位的和的个位构成的（即取余后的数）
            str.append((x + y + carry) % 10);
            //进位是（十位的数），如果三者和只有一位，则为0,两位就取十位上的数
            carry = (x + y + carry) / 10;
        }
        //反着加的，所以要倒回去
        return str.reverse().toString();
    }
}

相遇问题

462. 最少移动次数使数组元素相等 II（Easy）

给定一个非空整数数组，找到使所有数组元素相等所需的最小移动数，其中每次移动可将选定的一个元素加1或减1。您可以假设数组的长度最多为10000。

例如:

输入: [1,2,3]
输出: 2

说明：

只有两个动作是必要的（记得每一步仅可使其中一个元素加1或减1）：
[1,2,3] => [2,2,3] => [2,2,2]

解法一：题目意思是我们每次都可以将数组中的一个数加1或者减1，求数组元素变成一样的最少步骤，不难想到，我们只要找到这个数组的中位数即可，所以关键点在于如何找到中位数，最简单的，我们可以将这个数组排序，而两端的数字变成中间的一个数字需要的步数实际上就是两端数字的距离设 a <= x <= b，将 a 和 b 都变化成 x，则需要的步数为 x-a+b-x = b-a

class Solution {
    public int minMoves2(int[] nums) {
        //对数组排序
        Arrays.sort(nums);
        int move = 0;
        int l = 0;
        int h = nums.length - 1;
        //两个指针未相遇
        while (l <= h){
            move += nums[h--] - nums[l++];
        }
        return move;
    }
}

解法二：利用快速选择找到中位数，然后求步数，时间复杂度为O(n)，比排序的O(nlogn)要好

public int minMoves2(int[] nums) {
    int move = 0;
    int median = findKthSmallest(nums, nums.length / 2);
    for (int num : nums) {
        move += Math.abs(num - median);
    }
    return move;
}

private int findKthSmallest(int[] nums, int k) {
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int j = partition(nums, l, h);
        if (j == k) {
            break;
        }
        if (j < k) {
            l = j + 1;
        } else {
            h = j - 1;
        }
    }
    return nums[k];
}

private int partition(int[] nums, int l, int h) {
    int i = l, j = h + 1;
    while (true) {
        //在左边找到第一个大于pivot的值，右边找到第一个小于pivot的值，交换
        //最后pivot的左边小于它，右边大于它
        while (nums[++i] < nums[l] && i < h) ;
        while (nums[--j] > nums[l] && j > l) ;
        if (i >= j) {
            break;
        }
        swap(nums, i, j);
    }
    //将l放置正确的位置
    swap(nums, l, j);
    //返回pivot所处的位置
    return j;
}

private void swap(int[] nums, int i, int j) {
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

多数投票问题

169.多数元素（Easy）

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

输入: [3,2,3]
输出: 3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

解法一：某个元素出现次数超过n/2，那么排序之后的中位数肯定是该元素

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

解法二：可以使用一个变量count记录某个数字出现的次数，cur表示当前统计的数字，遍历数组，第一个数为count为1，当遇到相同的就count+1，不同的就count-1，当count为0的时候就统计另外一个数的出现次数，遍历完数组后cur就是多数。

class Solution {
    public int majorityElement(int[] nums) {
        int count = 0;
        int cur = nums[0];
        for (int num : nums) {
            //如果count为0，就更新cur
            if (count == 0){
                cur = num;
            }
            //cur == num就加一，否则减一
            if (cur == num){
                count++;
            }else {
                count--;
            }
        }
        return cur;
    }
}

解法三：使用快速选择，找到中间位置，直接返回，这种方法时间复杂度也为O(n)，但是代码比较复杂

class Solution {
    public int majorityElement(int[] nums) {
        return findKthSmallest(nums, nums.length / 2);
    }

    private int findKthSmallest(int[] nums, int k) {
        //快速查找
        int l = 0;
        int r = nums.length - 1;
        while (l < r){
            //分治，找出当前pivot的位置
            int position = partition(nums, l, r);
            if (position == k){
                break;
            }else if (position < k){
                l = position + 1;
            }else {
                r = position - 1;
            }
        }
        return nums[k];
    }

    private int partition(int[] nums, int l, int r) {
        int i = l + 1;
        int j = r;
        while (i < j){
            //复用l为pivot
            while (nums[i] < nums[l] && i < j){
                i++;
            };
            while (nums[j] > nums[l] && i < j){
                j--;
            };
            if (i > j){
                break;
            }
            swap(nums, i, j);
        }
        swap(nums, l, j);
        return j;
    }

    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

367. 有效的完全平方数（Easy）

给定一个正整数 num，编写一个函数，如果 num 是一个完全平方数，则返回 True，否则返回 False。说明：不要使用任何内置的库函数，如sqrt。

示例 1：

输入：16
输出：True

示例 2：

输入：14
输出：False

解法一：

对于一个数num来说，如果存在完全平方数，那么这个数肯定是小于num的整数，所以可以遍历1~num的整数，如果找到一个数n*n=num，那么num是完全平方数。
不出所料，这种解法超出时间限制。

class Solution {
    public boolean isPerfectSquare(int num) {
        int i = 1;
        boolean result = false;
        while (i < num){
            if (i * i == num){
                result = true;
            }
        }
        return result;
    }
}

解法二：通过观察可得，完全平方数1,4,9,16,...的间隔是3,5,7...，可以利用这个规律来判断某个数是否为完全平方数

class Solution {
    public boolean isPerfectSquare(int num) {
        int subNum = 1;
        while (num > 0){
            num -= subNum;
            //间隔递增间隔为2
            subNum += 2;
        }
        return num == 0;
    }
}

326. 3的幂（Easy）

给定一个整数，写一个函数来判断它是否是 3 的幂次方。

示例 1:

输入: 27
输出: true

示例 2:

输入: 0
输出: false

示例 3:

输入: 9
输出: true

示例 4:

输入: 45
输出: false

进阶：你能不使用循环或者递归来完成本题吗？

解法一：最容易想到的是使用循环来解决

class Solution {
    public boolean isPowerOfThree(int n) {
        if (n < 1) {
            return false;
        }

        while (n % 3 == 0) {
            n /= 3;
        }

        return n == 1;
    }
}

//用乘法会超时
public boolean isPowerOfThree(int n) {
    if (n == 1){
        return true;
    }
    int res = 1;
    while (res < n){
        res *= 3;
    }
    return res == n;
}

238. 除自身以外数组的乘积（Medium）

给定长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:

输入: [1,2,3,4]
输出: [24,12,8,6]
说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。

进阶：

你可以在常数空间复杂度内完成这个题目吗？（出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

题解：

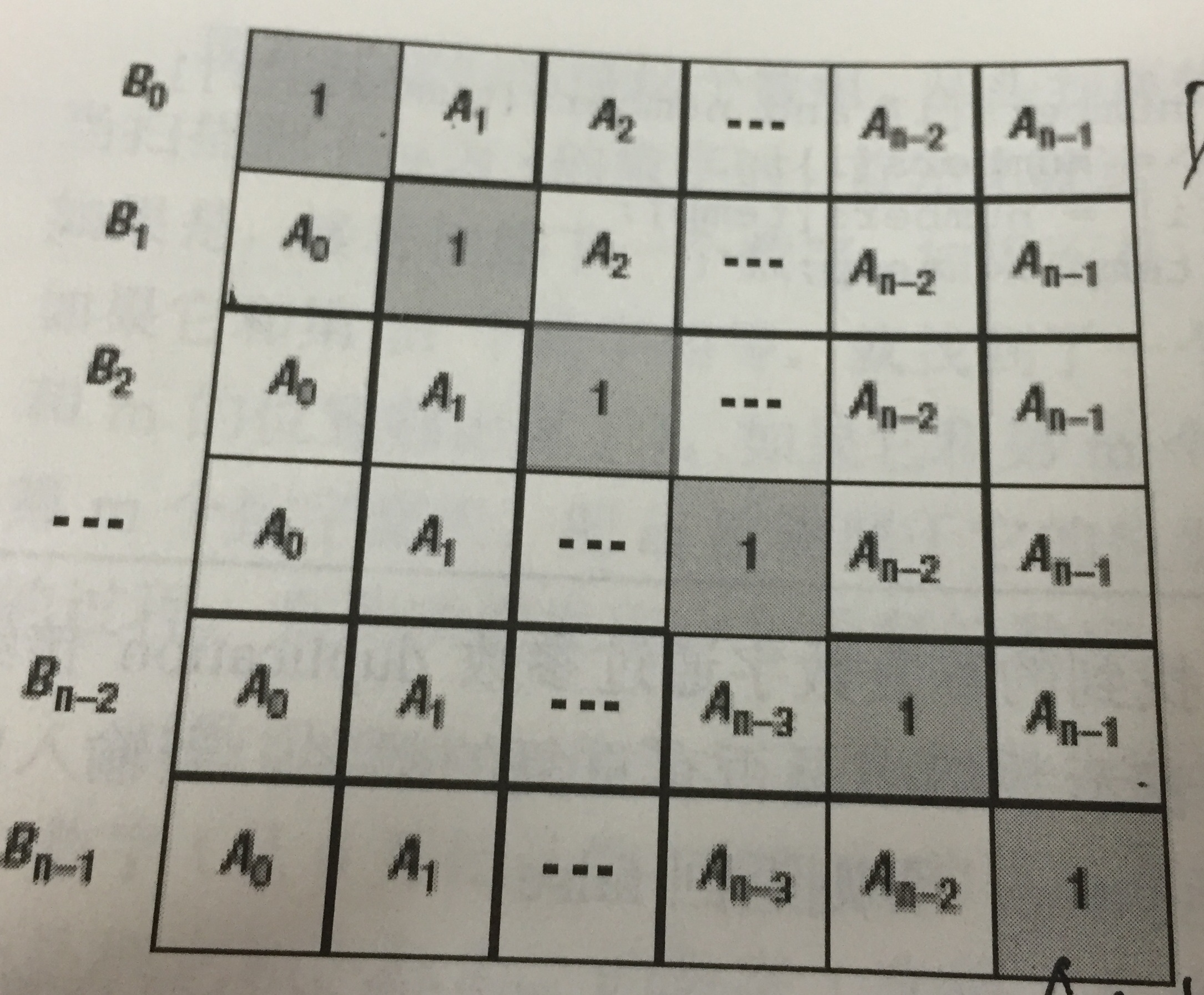
这道题的关键是要能想到output[i]等于左边乘积*右边乘积。画出图就是两个三角形，我们只需要计算出这两个三角形(即左右数之积)即可
从左遍历到右，计算出左边数的积，从右到左计算出右边数的积，只需两趟遍历就可以得出结果

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] products = new int[n];
        Arrays.fill(products, 1);

        int left = 1;
        //从左遍历到右
        for (int i = 1; i < n; i++) {
            //nums[i]左边积
            left *= nums[i - 1];
            //先给products[i]乘左边积
            products[i] *= left;
        }
        //从右遍历到左
        int right = 1;
        for (int i = n - 2; i >= 0; i--) {
            right *= nums[i + 1];
            products[i] *= right;
        }
        return products;
    }
}

628. 三个数的最大乘积（Easy）

给定一个整型数组，在数组中找出由三个数组成的最大乘积，并输出这个乘积。

示例 1:

输入: [1,2,3]
输出: 6

示例 2:

输入: [1,2,3,4]
输出: 24

注意:

给定的整型数组长度范围是[3,104]，数组中所有的元素范围是[-1000, 1000]。
输入的数组中任意三个数的乘积不会超出32位有符号整数的范围。

解法一：找数组中三个数组成的最大积，最容易想到的是先给数组排序，然后取最大的三个相乘，这种在全是正数或者全是负数的情况是正确的，但是在有正有负的情况就不对了，所以可以分这几种情况

全是正数，如{1,2,3,4}，排序之后取末尾三个相乘即可
全是负数，如{-3,-4,-1,-2}，排序之后是{-4,-3,-2,-1}，取后三个相乘
有正有负，如{-4,-3,1,2}，如果按照取末尾三个，积是-6，但却不是最大的，最大的是后两个相乘再加上末尾的2，得到24

class Solution {
    public int maximumProduct(int[] nums) {
        //排序
        Arrays.sort(nums);
        int n = nums.length;
        
        int a = Integer.MIN_VALUE;
        int b = Integer.MIN_VALUE;
        
        //如果有正有负
        if (nums[0] < 0 && nums[1] == 0){
            a = nums[0] * nums[1] * nums[n - 1];
        }
        
        //如果全正/全负
        b = nums[n - 1] * nums[n - 2] * nums[n - 3];
        return Math.max(a, b);
    }
}

解法二：总结出了最大积只可能是下面两种情况

3个最大数的乘积
两个最小数与一个最大数的乘积

那么可以准备5个变量，遍历数组，找到这几个变量即可

public class Solution {

    public int maximumProduct(int[] nums) {
        //准备3个最大值和2个最小值
        //假设max1 > max2 > max3
        int max1 = Integer.MIN_VALUE;
        int max2 = Integer.MIN_VALUE;
        int max3 = Integer.MIN_VALUE;
        //假设min1 < min2
        int min1 = Integer.MAX_VALUE;
        int min2 = Integer.MAX_VALUE;

        //遍历数组，寻找这5个值
        for (int num : nums) {
            //更新最大值
            if (num > max1){
                max3 = max2;
                max2 = max1;
                max1 = num;
            }else if (num > max2){
                max3 = max2;
                max2 = num;
            }else if (num > max3){
                max3 = num;
            }

            //更新最小值
            if (num < min1){
                min2 = min1;
                min1 = num;
            }else if (num < min2){
                min2 = num;
            }
        }
        return Math.max(max1 * max2 * max3, max1 * min1 * min2);
    }
}