此文为学习何晗老师《自然语言处理入门》笔记

由于词典分词无法消歧，如给定分词结果“商品和服务” 和 “商品和服务”，词典分词不知道哪种更合理。

统计自然语言处理的核心之一就是利用统计手法对语言建模。

语言建模

语言模型(Language Model, LM) 指的就是对语言现象的数学抽象。

比如一个句子 $w$ ，语言模型就是计算句子的出现概率 $p(w)$ 的模型。

概率分布就是统计某个人工标注而成的语料库。

把句子表示为单词列表 $w = w_1 w_2 \ldots w_k$ ，定义语言模型：

= p(w_1|w_0) \times p(w_2|w_0 w_1) \times \ldots \times p(w_{k+1}|w_0 w_1 w_2 \ldots w_k)

= \prod_{t=1}^{k+1}p(w_t|w_0 w_1 \ldots w_{t-1})

其中 $w_0=BOS$ (Begin Of Sentence, <s>)， $w_{k-1}=EOS$ (End Of Sentence， <\s>)。

比如“商品和服务”，概率估算如下：

p(商品和服务)=p(商品|BOS)p(和|BOS,商品)p(服务|BOS,商品,和)p(EOS|BOS,商品,和,服务)

我们使用极大似然估计(Maximum Likelihood Estimation, MLE)来计算每个后验概率：

p(w_t|w_0 \ldots w_{t-1}) = p_{ML}(w_0 \ldots w_{t-1}) = \frac {c(w_0 \ldots w_t)} {c(w_0 \ldots w_{t-1})}

其中 $c(w_0 \ldots w_t)$ 表示 $w_0 \ldots w_t$ 的计数。

这个语言模型会遇到两个问题：

数据稀疏 长度越大的句子越难出现，导致 $p(w_t|w_0 \ldots w_{t-1})$ 为0
计算代价大 k越大，上式中需要存储的 $p(w_t|w_0 \ldots w_{t-1})$ 就越多

马尔科夫链与二元语法

使用马尔科夫假设来简化语言模型：给定时间线上有一串事件顺序发生，假设每个事件的发生概率只取决于前一个事件，那么这串事件构成的因果链被称为马尔科夫链(Markov Chain)。

语言模型中，第 $t$ 个事件指的就是 $w_t$ 作为 $t$ 个单词出现，马尔科夫链假设每个单词现身的概率只取决于前一个单词：

p(w_t|w_0 \ldots w_{t-1})=p(w_t|w_{t-1})

= p(w_1|w_0) \times p(w_2|w_1) \times \ldots \times p(w_{k+1}|w_k)

= \prod_{t=1}^{k+1} \frac{count(w_t, w_{t-1})}{count(w_{t-1})}

n元语法

利用类似二元语法思路可以得到n元语法（n-gram）定义：每个单词的概率仅取决于该单词之前的n-1个单词。

p(w) = \prod_{t=1}^{k + n - 1}p(w_t|w_{t-n+1} \ldots w_{t-1})

特别的n=1称为一元语法（unigram），n=3为三元语法（trigram）

数据稀疏与平滑策略

n元模型的n越大，数据稀疏问题越严重。考虑到低阶n元语法更丰富，利用低阶n元语法平滑高阶n元语法。所谓平滑：是n元语法频次的折线平滑为曲线。

例如我们不希望二元语法 "商品货币" 的频次突然降到零，可以用一元语法 "商品" 和（或） "货币" 的频次去平滑它。下面是一种最简单的线性插值法（Linear Interpolation），它定义的二元语法概率:

p(w_t|w_{t-1}) = \lambda p_{ML}(w_t|w_{t-1}) + (1-\lambda)p(w_t)

类似的，一元线性插值：

p(w_t) = \lambda p_{ML}(w_t) + (1-\lambda) \frac {1} {N}

其中 $\lambda$ 是平滑因子， $N$ 是语料库总词数。

训练

语料库

语言模型只是一个函数的骨架，函数参数需要在语料库上统计得到。

人民日报语料库PKU
微软亚洲研究院语料库MSR
繁体中文分词语料库

训练

训练（train）指的是给定样本集（dataset，训练用的叫训练集）估计模型参数的过程。

对于二元语法模型，训练指的是统计二元语法频次以及一元语法频次，通过极大似然估计以及平滑策略，估计任意句子的概率分布，即得到了语言模型。

代码实现

假设word_count是一个collections.Counter对象，包含单词的统计数据（单词: 词频形式）

# TOKENS是分好词的文本列表
# 单个词频统计
words_count = Counter(TOKENS)
# 计算相邻的两个词词频
_2_gram_words = [
    TOKENS[i] + TOKENS[i+1] for i in range(len(TOKENS)-1)
]
_2_gram_word_counts = Counter(_2_gram_words)

def get_gram_count(word, wc):
    """
    获取词在wc中词频
    :param word 要统计的单词
    :param wc Counter类型的词频
    """
    if word in wc:
        return word_count[word]
    else:
        # 返回最小的词频
        return wc.most_common()[-1][-1]

def two_gram_model(sentence):
    """
    2-gram 模型计算
    :param sentence 话术
    """
    # cut为分词函数，得到一个分好的词列表
    tokens = cut(sentence)
    
    probability = 1
    
    # 根据上面的公式计算话术概率
    for i in range(1, len(tokens)):
        word = tokens[i]
        pre_word = tokens[i-1]
        
        _two_gram_c = get_gram_count(pre_word + word, _2_gram_word_counts)
        _one_gram_c = get_gram_count(pre_word, words_count)
        pro =  _two_gram_c / _one_gram_c
        
        probability *= pro
    
    return probability

示例

以以下三个文本为例

文本	分词列表
商品和服务	[商品, 和, 服务]
商品和服物美价廉	[商品, 和服, 物美价廉]
服务和货币	[服务, 和, 货币]

以 "始##始" 作为起始符，以 "末##末" 代表结尾

一元语法训练结果

词	词性	次数
和	n	2
和服	n	1
商品	n	2
服务	n	2
货币	n	1
物美价廉	n	1
BOS	begin	3
EOS	end	3

二元语法训练结果

以 @ 符号分隔二元语法中的两个单词

词	次数
和@服务	1
和@货币	1
和服@物美价廉	1
商品@和	1
商品@和服	1
服务@和	1
BOS@商品	2
BOS@服务	1
服务@EOS	1
货币@EOS	1
物美价廉@EOS	1

利用二元语法模拟性计算 "商品和服务"的概率

p(商品和服务)=p(商品|BOS)p(和|商品)p(服务|和)p(EOS|服务)

= \frac {2} {3} \times \frac {1} {2} \times \frac {1} {2} \times \frac {1} {2}

预测

预测（predict）是指利用模型对样本（句子）进行推断的过程，在中文分词任务中也就是利用模型推断分词序列。

词网

词网指的是句子中所有一元语法构成的网状结构，是HanLP工程上的概念。比如 "商品和服务" 这个句子，起始位置（offset）相同的单词写作一行，得到词网：

offset	分词
0	BOS
1	[商品]
2
3	[和, 和服]
4	[服务]
5	[务]
6	EOS

其中行5的 "务" 在一元语法中没有的词语，它是为了保证词网连通而添加的单字词语。

词网必须保证从起点出发的所有路径都会连通到终点。

词网中第 $i$ 行中长度为 $l$ 的单词与第 $i+l$ 行的所有单词互相连接，构成词图

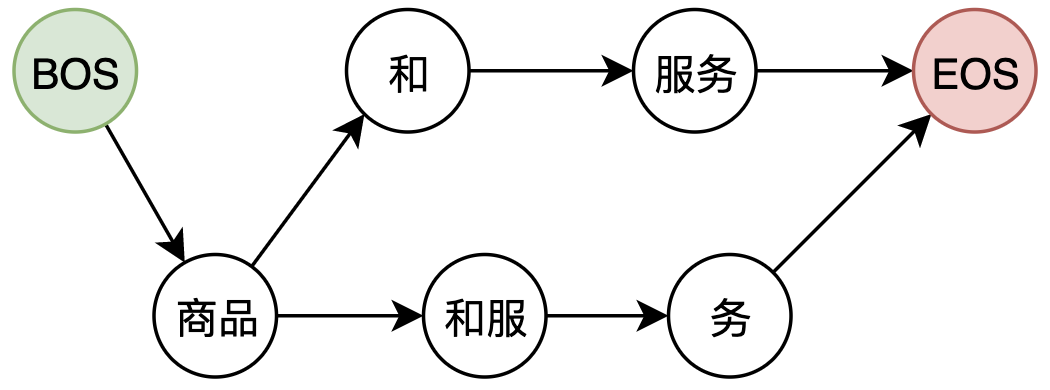
节点间距离计算

二元语法概率利用MLE辅以平滑策略得到如下中文分词中经常使用的经验公式：

\hat p(w_t|w_{t-1}) = \lambda [\mu \frac {c(w_{t-1} w_t)} {c(w_{t-1})}] + (1 - \lambda) \frac {c(w_t) + 1}{N}

其中， $\lambda, \mu \in (0, 1)$ 为两个不同的平滑因子。

考虑到多个 $(0, 1)$ 之间的浮点连续相乘后悔出现下溢出（等于0），因此工程上经常对概率取负对数，将浮点数乘法转化为负对数之间的加法：

\prod_{t=1}^{k+1} \hat p(w_t|w_{t-1}) \rightarrow - \sum_{t=1}^{k+1} \log \hat p(w_t|w_{t-1})

上图的词图计算距离后如下，最短的路径即为最优解：

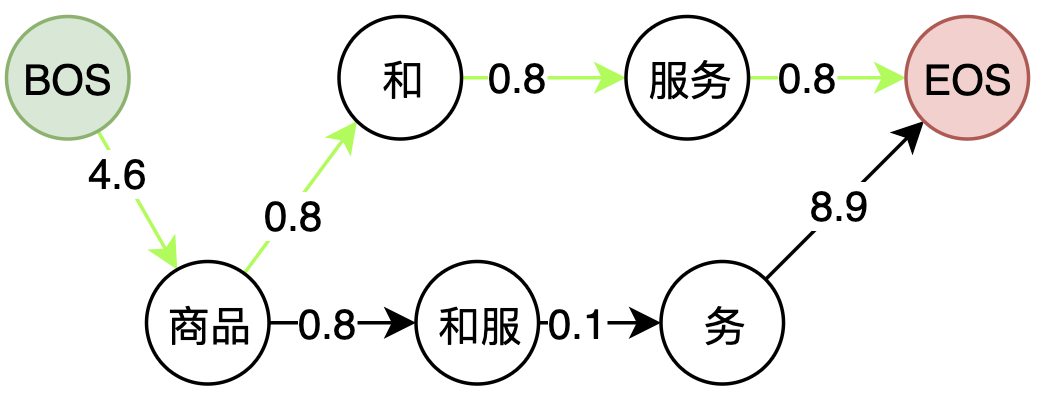
最短路径的计算：词图上的维比特算法

维比特算法（Viterbi Algorithm）步骤：

前向：由起点出发从前往后遍历节点，更新从起点到该节点的最小花费以及前驱指针
后向：由终点出发从后往前回溯前驱指针，取得最短路径

def viterbi(nodes):
    """
    维比特分词计算
    :param nodes 计算的分词词网
    """
    # 前向遍历，计算路径
    for i in range(len(nodes) - 1):
        # 遍历当前offset
        for node in nodes[i]:
            # 遍历当前节点的下一个offset列表，更新前驱指针
            for to in nodes[i + len(node.realWord)]:
                # 根据距离公式计算节点距离，并维护最短路径上的前驱指针from
                to.updateFrom(node)
    
    # 后向遍历，获取路径
    path = []
    # 从终点回溯
    f = nodes[len(nodes) - 1].getFirst()
    while f:
        path.insert(0, f)
        # 根据前驱指针from回溯
        f = f.getFrom()
    
    # 返回最短路径分词结果
    return [v.realWord for v in path]

/**
 * 更新weight最小的前驱词
 * @param from 前面的词
 */
public void updateFrom(Vertex from) {
    double weight = from.weight + calculateWeight(from, this);
    if (this.from == null || this.weight > weight) {
        this.from = from;
        this.weight = weight;
    }
}

/**
 * 从一个词到另一个词的词的花费
 *
 * @param from 前面的词
 * @param to   后面的词
 * @return 分数
 */
public static double calculateWeight(Vertex from, Vertex to) {
    int frequency = from.getAttribute().totalFrequency;
    if (frequency == 0) {
        frequency = 1;  // 防止发生除零错误
    }
    int nTwoWordsFreq = CoreBiGramTableDictionary.getBiFrequency(from.wordID, to.wordID);
    // 上面的计算公式
    double value = -Math.log(dSmoothingPara * frequency / (MAX_FREQUENCY) + (1 - dSmoothingPara) * ((1 - dTemp) * nTwoWordsFreq / frequency + dTemp));
    if (value < 0.0) {
        value = -value;
    }
    return value;
}

总结

n元语法模型从词语接续的流畅度出发，为全切分词网中的二元接续打分，进而利用维比特算法求解似然概率最大的路径。
OOV问题：OOV在最初的全切分阶段已经不可能进入词网了，故OOV召回仍是n元语法模型的硬伤。

自然语言处理入门笔记-> 二元语法与中文分词