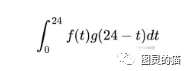
文章来自我的公众号和同名博客~欢迎关注

定义
基于上一篇文章的通俗化例子,我们从基本概念上了解了卷积,那么更严格的定义是怎样的呢?
从数学上讲,卷积只不过是一种运算,对于很多没有学过信号处理,自动控制的同学来说各种专业的名词可以不做了解,我们接着继续。本质上卷积是将二元函数卷成一元函数 ,俗称降维打击。
1. 怎么卷?
考虑到函数 f 和 g 应该地位平等,或者说变量
卷起来
2. 卷了有什么用?
可以用来做多位数乘法,比如:
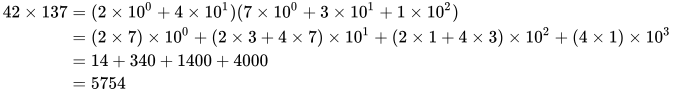
注意第二个等号右边每个括号里的系数构成的序列 (14,34,14,4),实际上就是序列 (2,4) 和 (7,3,1) 的卷积。在乘数不大时这么干显得有点蛋疼,不过要计算很长很长的两个数乘积的话,这种处理方法就能派上用场了,因为你可以用快速傅立叶变换 FFT 来得到卷积,比示例里的硬乘要快多了
有一个不太严谨的理解:
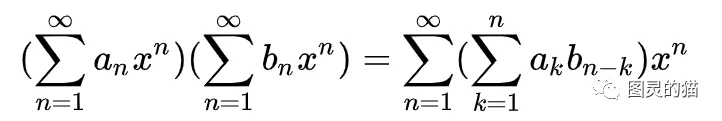
a对应着频率不同的
卷积的内核(涉及推导过程,可以跳过)
首先我们要理解这样一个概念:内积、积分、投影这三者其实从某个角度上讲是一个意思。
定义一组向量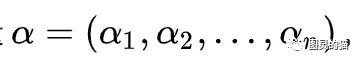 另一组向量
另一组向量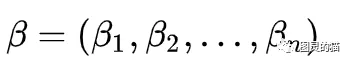
那么内积可以表达为:
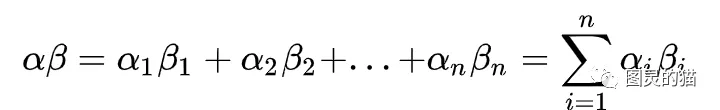
瞧,这即是内积,也是累加(积分)。投影的概念则可以理解为向量a在基向量b上的一组投影,坐标为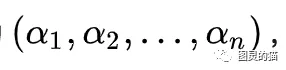
这和一个点在3D欧几里得空间的三轴投影坐标是一个道理。
这样,我们可以顺便先来看看Fourier变换在做什么:
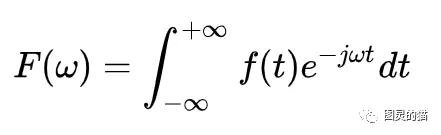
再引入一个完美的式子,欧拉公式:
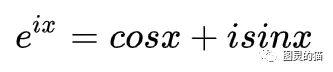
从Fourier的定义式可以看出是对f(t)和exp(-jwt)相乘后在无穷域上对其进行积分,那么其实就是将f(t)投影在exp(-jwt)上,如果不理解是什么鬼就变换为两个正交的三角函数(欧拉公式就在这里起作用~)
所以这就明朗了:Fourier把f(t)投影到了两个为正交关系的正弦和余弦空间中。也可以从周期信号的Fourier级数分解表达式更容易看出这个投影关系。
这个投影有点奇怪,它在投影之前先把g(
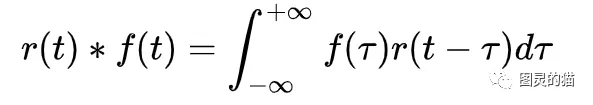
相当于在投影之前,先把输入信号r(t)在时间轴上翻转了180°,然后与系统f(t)进行投影。投影的概念我们可以很好理解,无论是向量内积运算相当于线投影,或者空间的一个多面体在三维空间平面上的投影面,这种投影运算就相当于一种重合面积。
如果从这个角度去看输入、系统和输出三者之间的关系,那么就可以从图形角度去理解为什么一个一阶系统在阶跃响应输出下是一条单调上升的曲线了。这里用一张wikipedia里关于卷积的一张图形化解释,想要了解更多的同学可以自行查阅相关教材
(感谢知乎学霸王尼莫的帮助)
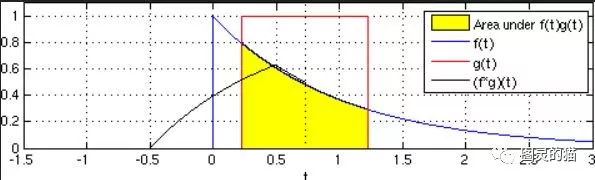

卷积的应用
用一个模板和一幅图像进行卷积,对于图像上的一个点,让模板的原点和该点重合,然后模板上的点和图像上对应的点相乘,然后各点的积相加,就得到该点的卷积值。对图像上的每个点都这样处理。
由于多数模板都对称,所以模板不旋转。卷积是一种积分运算,用来求两个曲线重叠区域面积。可以看作加权求和,可以用来消除噪声、特征增强。把一个点的像素值用它周围的点的像素值的加权平均代替。
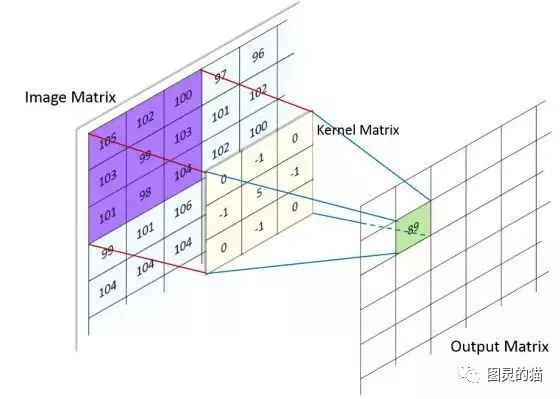
卷积也可以理解为一种线性运算,图像处理中常见的mask运算都是卷积,广泛应用于图像滤波。 卷积关系最重要的一种情况,就是在信号与线性系统或数字信号处理中的卷积定理。
利用该定理,可以将时间域或空间域中的卷积运算等价为频率域的相乘运算,从而利用FFT等快速算法,实现有效的计算,节省运算代价。
下面是来自sselssbh博客的一个例子,非常形象的解释了卷积在图像领域的作用
有这么一副图像,可以看到,图像上有很多噪点:
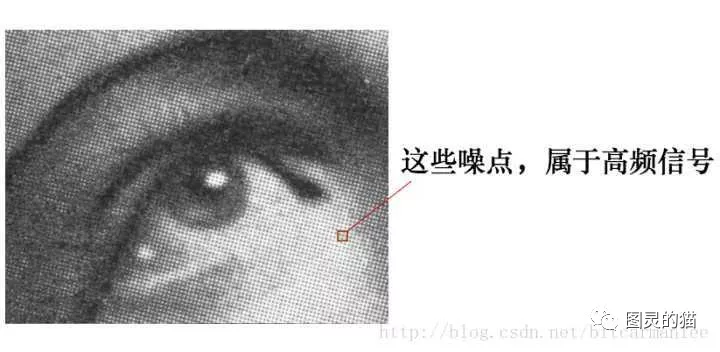
高频信号,就好像平地耸立的山峰:

看起来很显眼。平滑这座山峰的办法之一就是,把山峰刨掉一些土,填到山峰周围去。用数学的话来说,就是把山峰周围的高度平滑以下得到

卷积可以实现这个平滑算法。有噪点的原图,可以把它转为一个矩阵:

然后用下面这个平均矩阵(说明下,原图的处理实际上用的是正态分布矩阵,这里为了简单,就用了算术平均矩阵)来平滑图像:
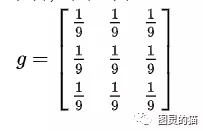
记得刚才说过的算法,把高频信号与周围的数值平均一下就可以平滑山峰。比如我要平滑a1,1 点,就在矩阵中,取出a1,1点附近的点组成矩阵 f ,和 g 进行卷积计算后,再填回去
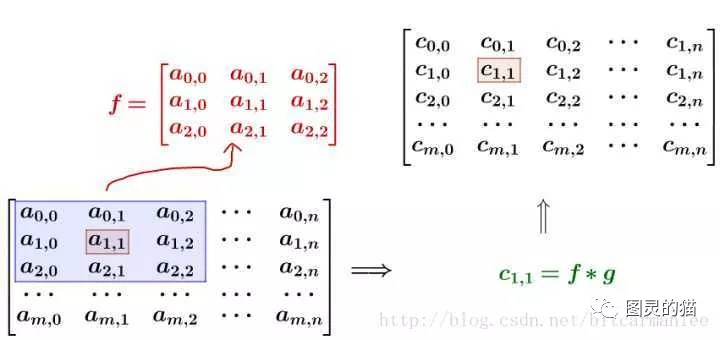
要注意一点,为了运用卷积, g虽然和f同维度,但下标有点不一样:

写成卷积公式就是:
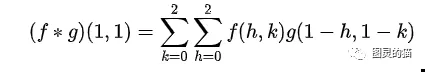
这样相当于实现了 g 这个矩阵在原来图像上的划动(准确来说,下面这个二维卷积的例子把 g 矩阵旋转了180∘ )

2维卷积
在图像识别中,2 维卷积是一个最常用,也是相当简单的操作:从卷积核开始,这是一个小的权值矩阵。这个卷积核在 2 维输入数据上「滑动」,对当前输入的部分元素进行矩阵乘法,然后将结果汇为单个输出像素。
立体的角度来看,二维层面的卷积就是移动和映射(自上而下)
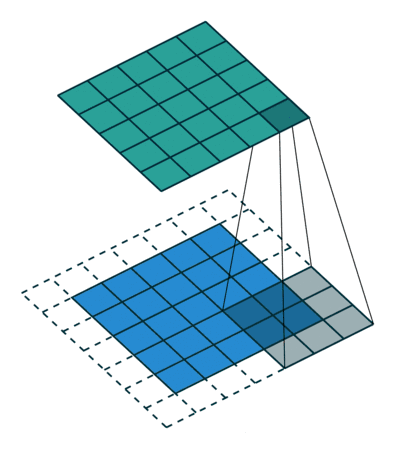
而从平面展开则是如下的过程,每一个蓝色9宫格的数字都对应了一个绿色各自的数字,这个对应过程就是卷积的具体计算。
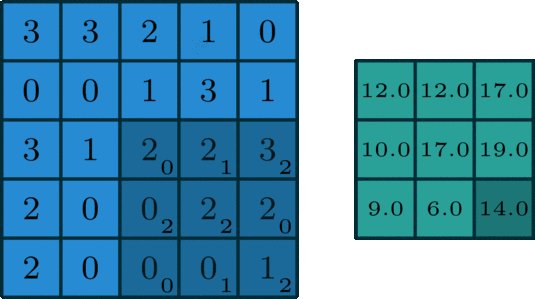
再比如做馒头
楼下早点铺子生意太好了,供不应求,就买了一台机器,不断的生产馒头。
假设馒头的生产速度是 f(t) ,那么一天后生产出来的馒头总量为:
馒头生产出来之后,就会慢慢腐败,假设腐败函数为 g(t) ,比如,10个馒头,24小时会腐败:
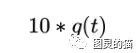
想想就知道,第一个小时生产出来的馒头,一天后会经历24小时的腐败,第二个小时生产出来的馒头,一天后会经历23小时的腐败。 如此,我们可以知道,一天后,馒头总共腐败了: