分治(Divide And Conquer)
分治,也就是分而治之。它的一般步骤如下
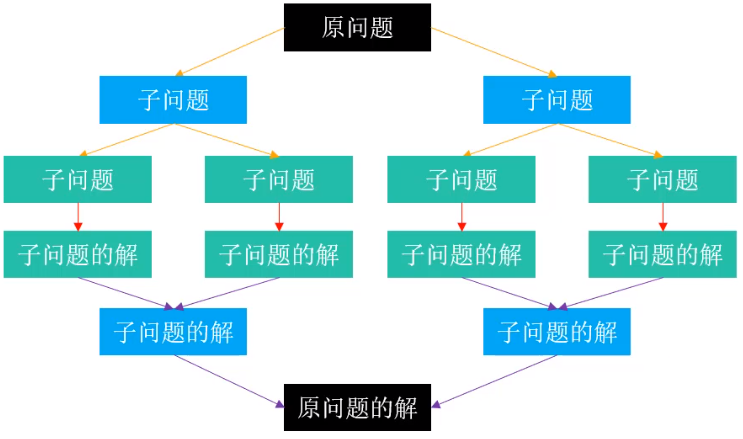
- 将原问题分解成为若干个规模较小的子问题(子问题和原问题的结构一样,只是规模不一样)
- 子问题又被分解成规模更小的子问题,直到不能再分解(直到可以轻易计算出子问题的解)
- 利用子问题的解推导出原问题的解
所以,通过上面介绍的步骤,可以知道,分治策略非常使用于递归,因为前面在将原问题分解为若干个子问题时,子问题的结构与原问题是一样的,只是规模不一样,所以,很容易想到,这可以利用递归来进行解决。
不过,需要注意一点的是,子问题之间是相互独立的
归并的应用
- 快速排序
- 归并排序
- Karatsuba算法(大数乘法)
主定理(Master Theorem)
分治策略通常遵守一种通用的模式
-
解决规模为n的问题,分解成a个规模为n / b的子问题,然后再O(n^d)时间内将子问题的解合并起来
-
所以,分治策略算法运行的时间有这样一个公式:T(n) = aT(n/b) + O(n^d),其中a > 0,b > 1,d≥0
- d > logb(a),T(n) = O(n^d)
- d = logb(a),T(n) = O(n^dlogn)
- d < logb(a),T(n) = O(n^(logb()a))
例如归并排序的运行时间是:T(n) = 2T(n / 2) + O(n),a = 2,b = 2,d = 1,所以T(n) = O(nlogn)
那么,为什么有些问题采用分治策略以后,性能会有所提升呢?
例如,前面在介绍冒泡排序,选择排序,插入排序时,都存在最坏时间复杂度,为n^2,但是后面使用快速排序,归并排序这些采用分治思想以后,发现算法的性能就会有所提升。
例如现在需要对n个数据进行排序,时间复杂度为O(n^2)
- 现在将n个数据平均分为2组,每一组的数据规模则为n / 2
- 现在对每一组数据进行单独排序,时间复杂度为O(n^2/4)
- 所以将两组数据进行排序,总共消耗的时间复杂度为O(n^2/2) + 合并需要的时间O(merge)
- 如果合并操作消耗的时间是小于O(n^2/2)的,这样得到的结果是小于对n个数据进行排序的
了解到了分治策略的基本原理以后,接下来就研究一下分治策略的几种应用场景
场景一:最大连续子序列和[Leetcode地址]
给定一个长度为n的整数序列,求它的最大连续子序列和
比如-2,1,-3,4,-1,2,1,-5,4的最大连续子序列和是4 + (-1) + 2 + 1 = 6
子序列:-2.4,2这样的序列,叫做子序列,不要求是连续的
连续子序列(也称为子串,子数组,子区间):,4,-1,2,1;即连在一起的子序列叫做连续子序列
这个问题,也属于最大切片问题(最大区段,Greatest Slice)
方法一:暴力出奇迹
穷举出所有可能的连续子序列,并计算出它们的和,最后取出它们中的最大值。
- 定义一个begin指针,从0位开始依次往右进行遍历
- 定义一个end指针,从0开始依次往右进行遍历
- end指针的索引大于等于begin指针
- 计算end到begin之间所有元素的和
集合这个思路,可以得到如下的代码
static int maxSubarray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int max = Integer.MIN_VALUE;
for (int begin = 0; begin < nums.length; begin++) {
for (int end = begin; end < nums.length; end++) {
int sum = 0;
for (int i = begin; i < end; i++) {
sum += nums[i];
}
max = Math.max(max,sum);
}
}
return max;
}
这种算法的空间复杂度为:O(n^3),空间复杂度为:O(1)
很明显,上面这种算法有很多重复的计算,就在最内层的循环中,当begin指针不变时,end指针往右移动,往右移动的过程中,begin到end之间的的元素,其实是存在重复计算的,所以首先,可以从这里进行优化,优化后的结果如下
static int maxSubarray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int max = Integer.MIN_VALUE;
for (int begin = 0; begin < nums.length; begin++) {
int sum = 0;
for (int end = begin; end < nums.length; end++) {
sum += nums[end];
max = Math.max(max,sum);
}
}
return max;
}
这样,就可以将时间复杂度从O(n^3)降为O(n^2)。不过虽然这种方法也可以解决上面的问题,但是效率并不高,接下来用分治的方法进行尝试。
方法二:分治
将序列[begin,end)均匀得分割成2个子序列[begin,mid),[mid,end),其中mid = (begin + end) >> 1
现假设问题的解存在于区间[i,j)中,那么问题的解有以下三种可能
- [i,j)存在于[begin,mid)中
- [i,j)存在于[mid,end)中
- [i,j)一部分存在于[begin,mid)中,另一部分存在于[mid,end)中
- 这种情况下[i,j) = [i,mid) + [mid,j)

最终,通过这种思路,得到的代码如下
static int maxSubarray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
return maxSubarray(nums,0,nums.length);
}
//计算[begin,end),最大连续子序列的和
static int maxSubarray(int[] nums,int begin, int end) {
if (end - begin < 2) return nums[begin];
int mid = (begin + end) >> 1;
int leftMax = Integer.MIN_VALUE;
int leftSum = 0;
for (int i = mid - 1; i >= begin; i--) {
leftSum += nums[i];
leftMax = Math.max(leftMax,leftSum);
}
int rightMax = Integer.MIN_VALUE;
int rightSum = 0;
for (int i = mid; i < end; i++) {
rightSum += nums[i];
rightMax = Math.max(rightMax,rightSum);
}
int max = leftMax + rightMax;
return Math.max(max,Math.max(maxSubarray(nums,begin,mid),maxSubarray(nums,mid,end)));
}
通过这种优化,空间复杂度为O(logn),时间复杂度为O(nlogn)
场景二:大数乘法
在平时开发中,大家可能都是利用这种方式进行乘法计算的
int a = 10;
int b = 20;
int c = 2 * c;
使用符号*来进行运算。
但是,如果需要对两个超大的数(如100位的数组),就不能再利用*符号直接相乘了。因为
- 本来大操作树,现在在内存中就已经溢出了,在当前编程语言提供的基本数据类型中,不足以存储这么大数值的数字
- 相乘以后的结果可能会溢出
所以,一般来讲,如果要存储这么大的数据的话,首先采用字符串来进行存储,所以,最终计算出来的结果,依然是字符串
那么,2个超大是数相乘,应该 如何进行呢?
其实,可以按照小学学习的乘法运算,例如对36 * 54进行计算,按照小学的乘法运算,计算步骤如下
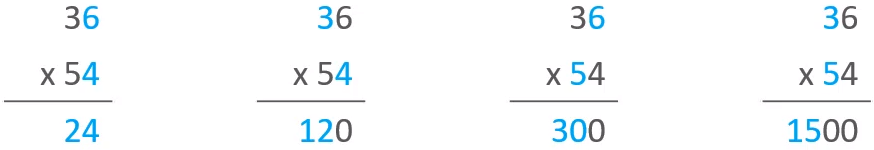
得到这些结果以后,然后将这些结果分别进行相加,得到结果如下
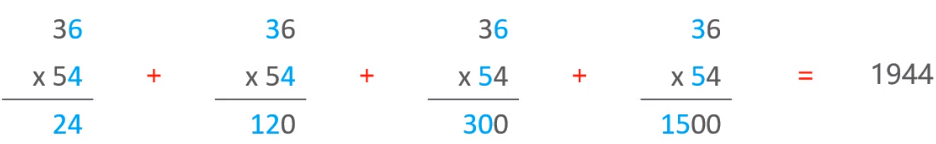
但是,需要注意,在进行大数乘法时的相加不是直接相加,如下图

现在假设上图是两个大数进行相乘,如果相乘后的每一位结果依然是直接相加的话,依然会导致内存溢出,所以应该每一位的结果单独相加,这样才能保证不会内存溢出。
而且,通过上面的简单试可以看出,2位数与2位数之间的相乘,进行了4次个位数的相乘,推导出3位数与3位数之间相乘,进行了9次个位数的相乘,所以在进行n位数与n位数之间的相乘时,需要大约进行n^2次个位数的相乘。所以相乘的每一步,可以利用分治思想来进行解决,所以模拟两个树进行相乘的示意图如下
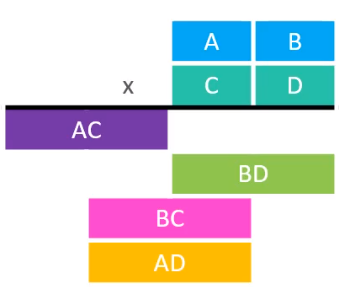
通过这种方式进行计算的消耗的时间表达式为T(n) = 4T(n/2) + O(n),所以时间复杂度为O(n^2)
大数乘法优化
Anatolii Alexeevitch Karatsuba于1960年提出Karatsuba算法,提高了大数乘法的效率
在前面,利用分治思想计算大数的话,基本思路如上图,Karatsuba算法基于数学公式进行了优化,公式为B * C + A * D = A * C + B * D - (A - B) * (C - D),通过这个数学公式,进行计算会得到怎样的优化呢?
结合上面的公式,就可以将上面的BC + AD进行拆解,最终拆解的结果如下
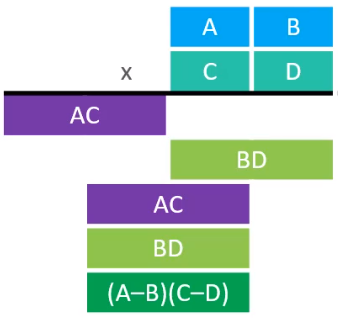
通过这样的优化,就可以减少两个大数相乘的次数,因为AC,BD的计算结果可以得到复用
所以,现在通过这种方式进行计算的话,消耗的时间表达式为T(n) = 3T(n/2) + O(n),利用主定理可以推导出时间复杂度为O(n^1.585)。这样就降低了复杂度
所以,大数乘法也是分治的一种应用,并且可以发现,如果一个问题一旦可以使用分治来进行解决的话, 大多数情况下,都是可以降低复杂度的。
完!