相关文献:
learning to rank : en.wikipedia.org/wiki/Learni… MRR: en.wikipedia.org/wiki/Mean_r… Precision and Recall: en.wikipedia.org/wiki/Precis… chales‘blog : charleshm.github.io/2016/03/Mod…
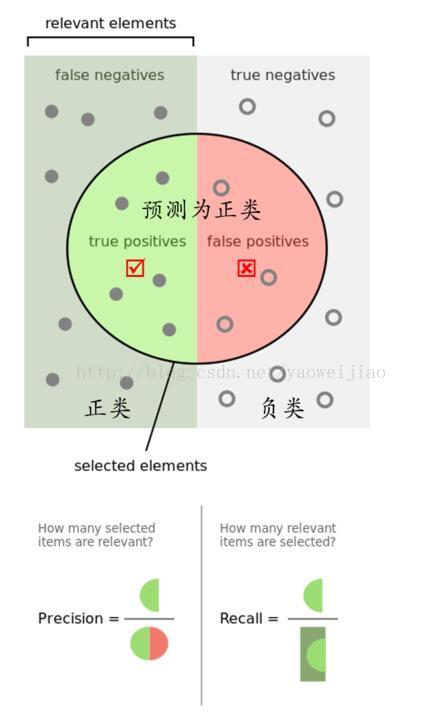
一 查准率与查全率
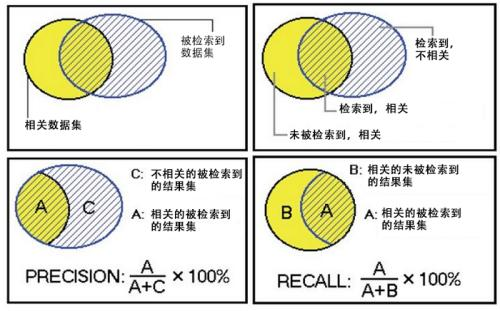
Precision(P)
是指检索得到的文档中相关文档所占的比例,公式如下:
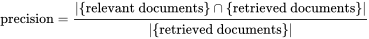
Recall: (R)
查全率率是指所有相关文档中被召回到的比例,公式如下:
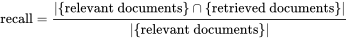
即使仅仅观察查全率为100% 也没多大意义, 虽然相关的文档 被全部召回了, 但是往往代价是伴随着更多的不相关文档被召回,导致查准率下降, 所以应该同时考虑两个指标,尽可能的都要高。
F-measure
一种同时考虑准确率和召回率的指标。公式如下:
可以看出F的取值范围从0到1。另外还有一种F的变体如下所示:
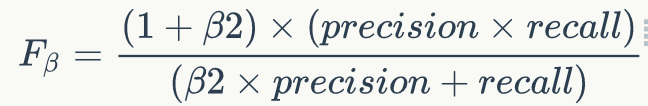
常用的两种设置是和
,前者中recall重要程度是precision的两倍,后者则相反,precision重要程度是recall的两倍。
二 Mean average precision(MAP)
准确率和召回率都只能衡量检索性能的一个方面,最理想的情况肯定是准确率和召回率都比较高。当我们想提高召回率的时候,肯定会影响准确率,所以可以把准确率看做是召回率的函数,即:,也就是随着召回率从0到1,准确率的变化情况。那么就可以对函数
在R上进行积分,可以求P的期望均值。公式如下:
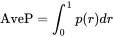
微分:
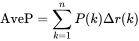
其中k是召回文档中的某doc rank位置, n是所有召回文档数,为cut-off
in the list准确率,
为
到
的召回率变化量
等价于下面的公式:
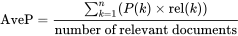
值为0或1,如果doc k是相关文档,
为1,否则为0,
AvePAveP的计算方式可以简单的认为是:
其中表示相关文档的总个数,
表示,结果列表从前往后看,第rr个相关文档在列表中的位置。比如,有三个相关文档,位置分别为1、3、6,那么
。在编程的时候需要注意,位置和第i个相关文档,都是从1开始的,不是从0开始的。
意义是在召回率从0到1逐步提高的同时,对每个R位置上的P进行相加,也即要保证准确率比较高,才能使最后的
比较大。
最后~,MAP计算所有Query的平均准确率分数:
Q为query数目总量。
三 Mean reciprocal rank(MRR)
where refers to the rank position of the first relevant document for the i-th query.
第一个正确答案的排名的倒数。MRR是指多个查询语句的排名倒数的均值

四 Expected reciprocal rank (ERR)
一种考虑是,一个文档是否被用户点击和排在它前面的文档有很大的关系,比如排在前面的文档都是不相关文档,那么它被点击的概率就高,如果排它前面的文档都是非常相关的文档,那么它被点击的概率就很低。Cascade Models假设用户从排名由高到底依次查看文档,一旦文档满足了用户的需求,则停止查看后续的文档。用RiRi表示用户只看在位置ii上的文档后就不在需要查看其它文档的概率,显然文档的相关度越高,越大。那么用户在位置i停止的概率公式如下:
ERR表示用户的需求被满足时停止的位置的倒数的期望。首先是计算用户在位置rr停止的概率,如下所示:
其中是关于文档相关度等级的函数,可以选取如下的函数:
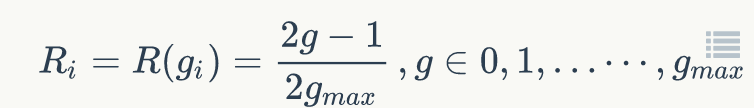
那么ERR的计算公式如下:
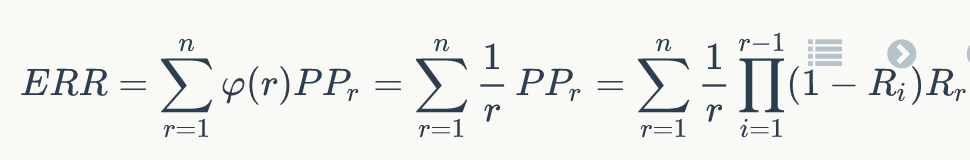
更通用一点,ERR不一定计算用户需求满足时停止的位置的倒数的期望,可以是其它基于位置的函数,只要满足
,且
随着
。比如DCG中的
ERR论文: web.archive.org/web/2012022…
五 Discounted cumulative gain (DCG)
在MAP计算公式中,文档只有相关不相关两种,而在nDCG中,文档的相关度可以分多个等级进行打分。
Cumulative Gain (CG)
计算DCG之前先进行计算CG, 公式如下:
是位置i处的相关性,上述公式计算了前p个结果的相关性总和
注意到召回结果的doc间任意排序,对CG函数值是无影响的,比如: 召回的三个文档rank依次是doc1,doc2,doc3,相关性依次是 3,2,0,而如果
rank顺序为doc3,doc2,doc1,其CG值依然为5. 而前者排序是最合理的,但CG值相同。
Discounted Cumulative Gain(DCG)
所以要引入对位置信息的度量计算,既要考虑文档的相关度等级,也要考虑它所在的位置信息。假设每个位置按照从小到大的排序,
它们的价值依次递减,意味着,相关度越高的如果排序越靠后,那么分数就应该受到惩罚,
可以假设第i个位置的价值是,那么排在第i个位置的文档所产生的效益就是
,公式如下:
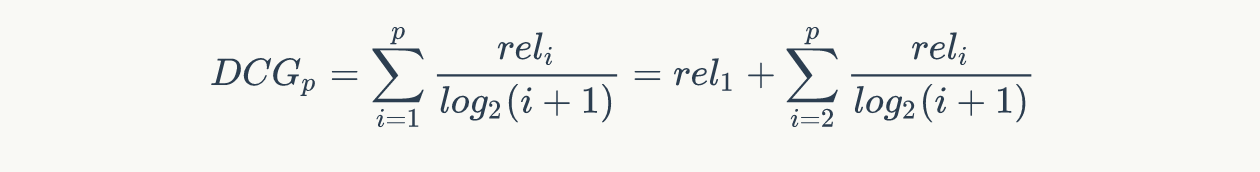
另一种比较常用的,用来增加相关度影响比重的DCG计算方式是:
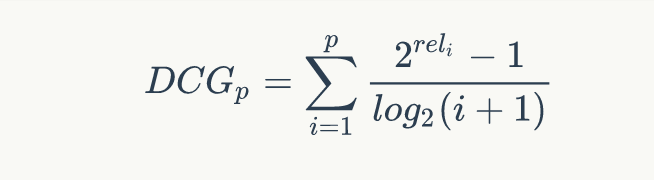
Normalized DCG (NDCG)
由于每个查询语句所能检索到的结果文档集合长度不一,p值的不同会对DCG的计算有较大的影响。所以不能对不同查询语句的DCG 进行求平均,需要进行归一化处理。nDCG就是用IDCG进行归一化处理,表示当前DCG比IDCG还差多大的距离。公式如下:
IDCG为理想情况下最大的DCG值
其中表示,文档按照相关性从大到小的顺序排序,取前p个文档组成的集合。也就是按照最优的方式对文档进行排序。
如何计算
假如一个query召回的文档前6个为
相关性分值依次为
意味着
的相关性分值为3,
相关性分值为2,以此类推。
值为:
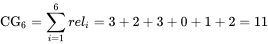
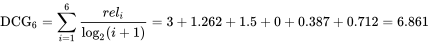
局限性
- nDCG不能惩罚“坏”文档,比如两个query返回了两列结果,分值分别为
,
那么两者的nDCG是一样的。注意把
,
,
映射为分值数字最好为
,而不是类似于
- nDCG不能惩罚“缺失” 的doc,比如两个query返回了两列结果,分值分别为
,
.前者计算
,后者计算
的话,两个doc都可以被认为是好的。解决方法是应该采取固定的topk大小来计算
,并在doc不足的query召回结果后面补上“最小权重分值”,如
,
两者均计算
六 分类模型上 Precision 和 Recall的含义
混淆矩阵
True Positive(真正, TP):将正类预测为正类数. True Negative(真负 , TN):将负类预测为负类数. False Positive(假正, FP):将负类预测为正类数 →→ 误报 (Type I error). False Negative(假负 , FN):将正类预测为负类数 →→ 漏报 (Type II error).

精确率(precision)定义为:
需要注意的是精确率(precision)和准确率(accuracy)是不一样的,
在正负样本不平衡的情况下,准确率这个评价指标有很大的缺陷。比如在互联网广告里面,点击的数量是很少的,一般只有千分之几,如果用acc,即使全部预测成负类(不点击)acc 也有 99% 以上,没有意义。
召回率(recall,sensitivity,true positive rate)定义为:
此外,还有 F1F1 值,是精确率和召回率的调和均值,
精确率和准确率都高的情况下,F1F1 值也会高。
通俗版本
实际上非常简单,精确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是对的。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP)。 而召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN)。