autograd是pytorch中自动计算微分的模块,官网文档在介绍中称为为
an engine for computing vector-Jacobian product
但是给的例子却解释的不是很清楚,下文通过一个例子进行进一步解释,解释之前了解一下什么是雅可比矩阵
Jacobian matrix(雅可比矩阵)
Y = G(X) Y是一个向量,X是一个向量,Y对X求导结果就是雅可比矩阵,即 雅可比矩阵
是一阶偏导数以一定方式排列成的矩阵,长这个样子
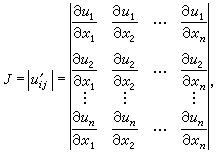
输出是向量(U1,U2......Un) 输入是(X1,X2......Xn)
例子
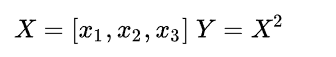
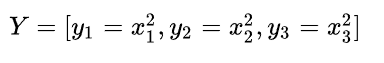
求得的雅可比矩阵是
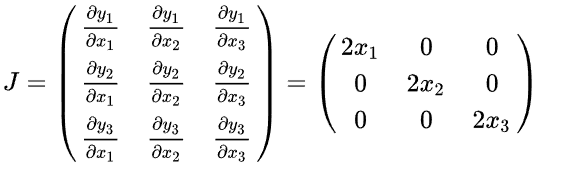
重点来了,问Y对X1的偏导数是多少?
这里面很显然就是第一列,(2x1,0,0)这一列,此时这个向量每个值代表分量函数对下X1的求导结果,而且此时三个分量函数求导结果的权重都是1。
如果,每个分量函数对X1的求导结果权重不是1,改成,y1是2,y2是1,y3是1,则问题Y对X1的偏导数是多少?的结果是(4x1,0,0),此时向量(2,1,1)理解成求导结果权重表达,此向量就是我们今天探讨的vector-Jacobian product中的vector,Jacobian自然指的是雅可比矩阵,
Torch代码验证
>>> x1=torch.tensor(1, requires_grad=True, dtype = torch.float)
>>> x2=torch.tensor(2, requires_grad=True, dtype = torch.float)
>>> x3=torch.tensor(3, requires_grad=True, dtype = torch.float)
>>> y=torch.randn(3) # produce a random vector for vector function define
>>> y[0]=x1**2+2*x2+x3 # define each vector function
>>> y[1]=x1+x2**3+x3**2
>>> y[2]=2*x1+x2**2+x3**3
>>> y.backward(torch.ones(3))
>>> x1.grad
tensor(5.)
>>> x2.grad
tensor(18.)
>>> x3.grad
tensor(34.)
各分量函数梯度的权重是v = (1,1,1)
则vector-Jacobian product 为
J*v = 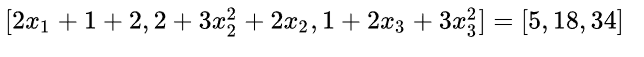
与代码实验结果相符