什么是二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法,前提是数据结构必须先排好序,可以在数据规模的对数时间复杂度内完成查找。但是,二分查找要求线性表具有有随机访问的特点(例如数组),也要求线性表能够根据中间元素的特点推测它两侧元素的性质,以达到缩减问题规模的效果。
二分查找问题也是面试中经常考到的问题,虽然它的思想很简单,但写好二分查找算法并不是一件容易的事情。
tips:数据必须是有序,也就是说排好序
不懂?没关系,下面我来将它讲解通俗易懂一些。
先来看一个数组:
let arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
如果我要找到第六个数5的索引,怎么找?这不废话嘛......
let target = 5;
for(let i = 0, len = arr.length; i < len; i++){
if(arr[i] == target){
return i;
}
}
然后我们分析一下这段代码,假设数组的长度为n,就要找n次,时间复杂度为O(n)。如果数据量很大呢?100个,1000个,10000个;甚至10万个更多。那时间复杂度是不是就跟着线性往上涨了?这时候二分查找就派上用场了。
二分查找基础思路
tips:因为数据是排好序的,所以我们可以这么干。(这里中位数的索引用mid表示)
1.用两个指针,一个指向第一个数,left = 0,一个指向最后一个数,right = arr.length - 1
2.然后再取中位数,判断该中位数 arr[mid] 和目标值 target 的大小
3.如果中位数刚好是需要找的那个数,直接返回索引mid,如果大于目标值呢?因为数组有序,肯定在中位数的前面,即0到(mid-1),如果小于目标值呢?因为数组有序,肯定在中位数的后面,即 mid+1 到数组的最后一位。所以,如果目标值在数组的前半部分,缩小右边界,right = mid - 1。如果目标值在数组的后半部分,缩小左边界,left = mid + 1。
4.然后枚举上面三步,关键是什么时候停止呢?你想一下,每次搜索范围减少一半,当left = right的时候,说明搜索范围已经是一个数了,不能再缩小了,再缩小就可以停止了。
let target = 5;
let left = 0
let right = arr.length - 1;
while(left <= right){
let mid = Math.floor((right + left) / 2)
if(arr[mid] === target){ //找到目标值
return mid;
}else if(arr[mid] > target){ //比目标值大,说明数在前半部分,缩小右边界
right = mid - 1;
}else{ //比目标值小,说明数在后半部分,缩小左边界
left = mid + 1;
}
} 根据目标值和中位数的比较,不断的缩小搜索数据的范围,每次可以减小一半的搜索范围,所以时间复杂度为 log n,如果数据量大,这种二分法效率是非常高的。同学们可以自己去验证。
二分查找进阶思路
左边界
现在我们把数组改成这样子
let arr = [0, 1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 9]
或者这样子
或者
let arr = [...........这个数组非常的长,里面的值非常的大]
问题变成怎么找到第一个5和最后一个5呢?用上面的方法可行嘛?显然是不行的。
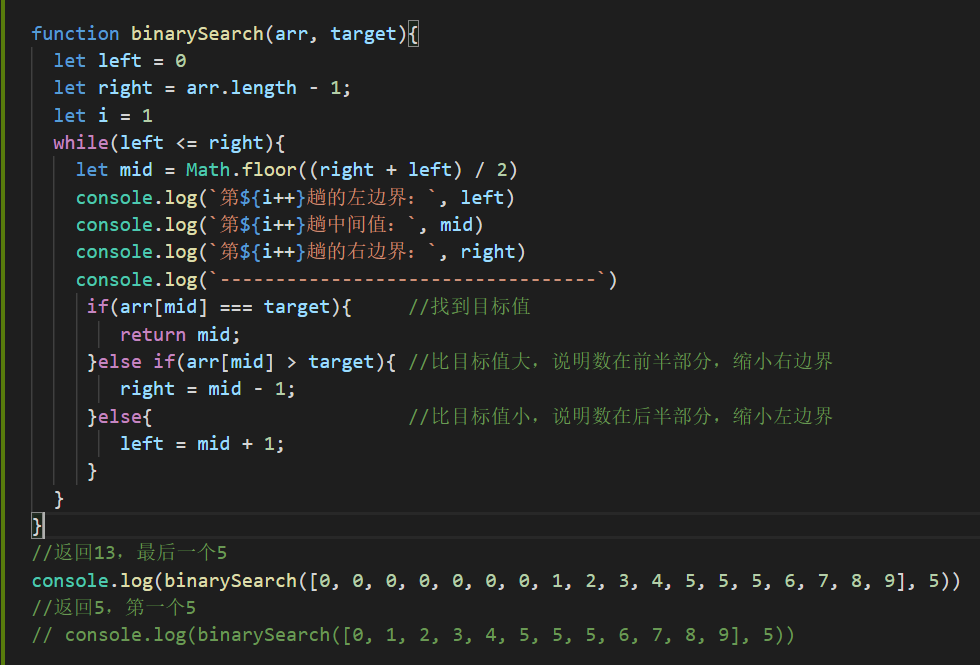
第1趟的左边界: 0
第2趟中间值: 8
第3趟的右边界: 17
----------------------------------
第4趟的左边界: 9
第5趟中间值: 13
第6趟的右边界: 17
----------------------------------
13很明显通过上面的测试,是满足不了要求的,每次都是在缩小边界的同时只需要找到一个满足条件的就退出了。那我们能不能修改一下,满足边界的时候先不退出,再通过收缩左右的边界来达到找到第一个或者最后一个的要求,答案是肯定的,那怎么修改代码呢?别着急,慢慢来
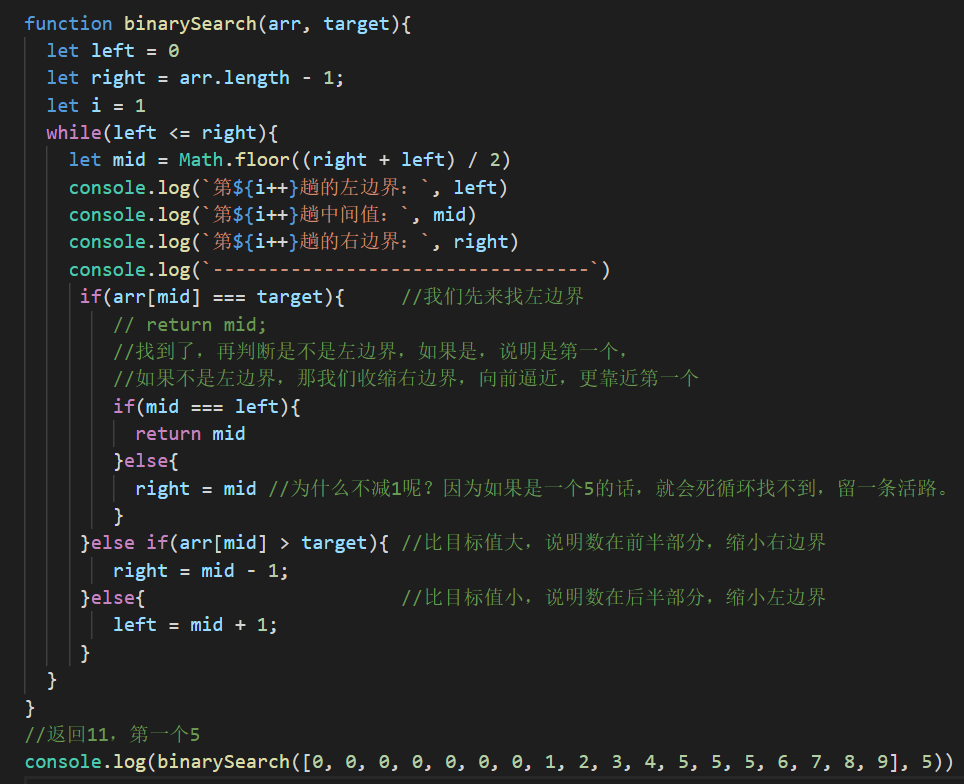
第1趟的左边界: 0
第2趟中间值: 8
第3趟的右边界: 17
----------------------------------
第4趟的左边界: 9
第5趟中间值: 13
第6趟的右边界: 17
----------------------------------
第4趟的左边界: 9
第5趟中间值: 13
第6趟的右边界: 17
----------------------------------
第4趟的左边界: 9
第5趟中间值: 13
第6趟的右边界: 17
----------------------------------
第4趟的左边界: 9
第5趟中间值: 13
第6趟的右边界: 17
----------------------------------
11右边界
同理,右边界是一样的,只需要判断的时候收缩左边界
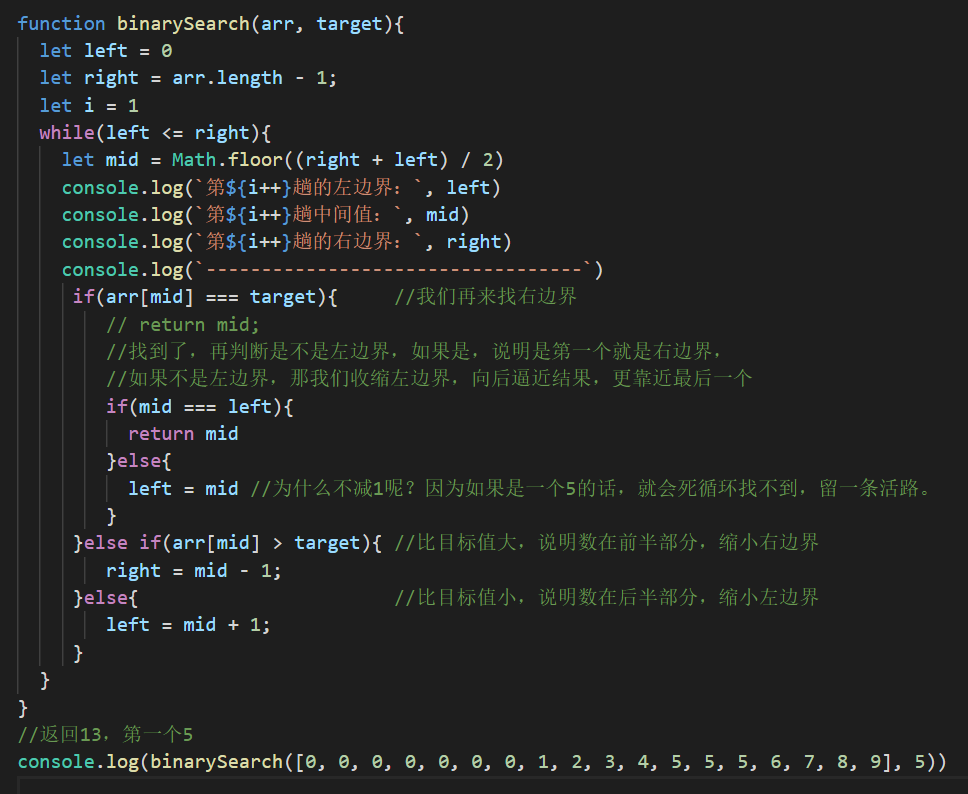
tips:还有一个问题,let arr = [...........这个数组非常的长,里面的值非常的大] 怎么办?
事实上,let mid = left + (right - left) / 2 在 right 很大、 left 是负数且很小的时候, right - left 也有可能超过 int 类型能表示的最大值,只不过一般情况下 left 和 right 表示的是数组索引值,left 是非负数,因此 right - left 溢出的可能性很小。
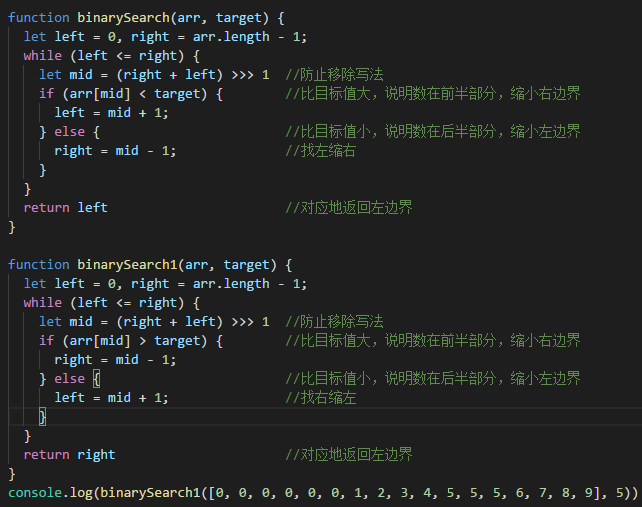
推荐下面两种写法
let mid = (left + right) >>> 1 ;
let mid = left + (right - left) / 2;其实我们没必要这么麻烦,可以直接这样写,把区间锁死在[left, right],必然会有一个是刚好是第一个等于目标值,另一个刚好不等于目标值。直接看代码和注释。

对应的我们优化一下代码
总结
到这里,你已经掌握了二分法的细节和模板了,稍加练习你就可以很熟练。其实上面的写法是很基础的,可以优化一下只需要if else 两个判断语句就可以了。优化就当做同学作业啦~赶紧练练吧~
这里给一个网上的模板,其实就是一句话。左加右不加,找右缩左,找左缩右。可以思考下为什么?
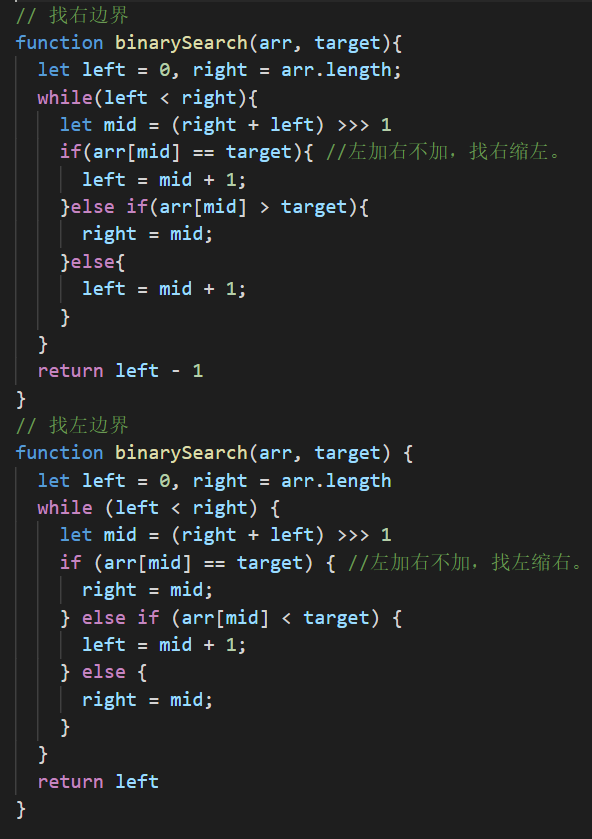
模版解释:
一开始我也无法理解为什么要这么写。这么写有什么好处?优化判断条件。
首先对于上面的基础写法和模版,基础写法只适合寻找一个值,终止条件是right != left,而搜索区间是【left,right】,当【2,3】或者【3,2】的时候才会终止循环。这样的话就要在等于的时候多做些判断,判断条件太多。
对于模版写法,搜索区间是[left, right),左闭右开。终止条件是right == left。你完全可以这样理解:
搜索左边界:因为是左闭右开,当mid为目标值的时候,收缩右边界,让目标值尽可能的往左边靠。
搜索右边界:因为是左闭右开,当mid为目标值的时候,收缩左边界,让目标值尽可能的往右边靠。
更加详细的请参考链接:leetcode-cn.com/explore/lea…