相对于红黑树的新增节点,删除就更复杂了。
要想删除一个节点,需要先找到这个节点,删除之后调整红黑树,使红黑树再平衡。
public V remove(Object key) {
Entry<K,V> p = getEntry(key); // ①
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p); // ②
return oldValue;
}
①:找到要删除的节点
②:删除该节点
但是这里的删除节点并不是直接删除,而是使用替换的方法,分3种情况:
- 没有子节点。无需替换,直接删除。
- 有一个子节点。用子节点替换该节点即可。
- 有2个子节点。这时就比较复杂了,节点删除后,这个空位由谁来顶替。打个比方,老头子死了,没立遗嘱,遗产由哪个子女继承?JDK8中使用后继节点的方法,来确定继承人。
后继节点可能有一个子节点(符合情况2),也可能没有子节点(符合情况1)。
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p); // ①
p.key = s.key; // ②
p.value = s.value;
p = s;
} // p has 2 children
①:p有两个子节点,符合情况3,获取p的后继节点。
②:执行替换
后继节点(successor)
后继节点:大于指定节点的最小节点
与之相对应的,有个前继节点小于指定节点的最大节点。
后继节点的确认
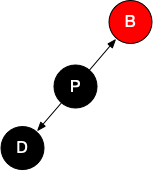
网上看到一种方法,投影法,将树的节点投影到坐标轴上。如图所示:
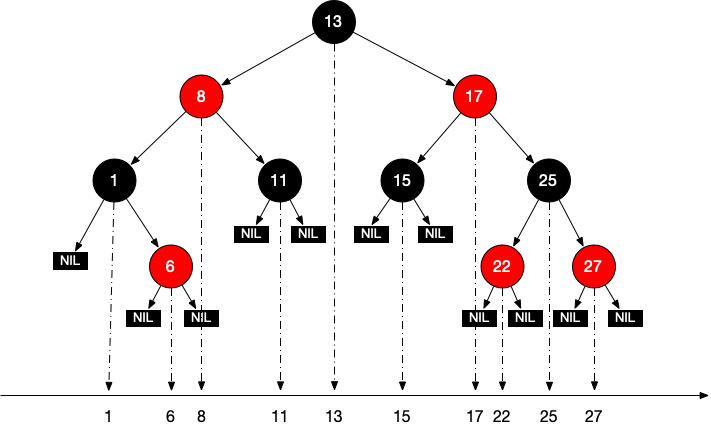
后继节点就是所选节点坐标轴上后面一个坐标,如17的后继节点就是22。前继节点就是前面一个坐标。
用代码来实现就是,
- 如果节点有右子节点,则后继节点就是右子树中最小的节点。
- 如果节点没有右子节点,后继节点为某祖先节点,从当前节点往上找,如果它是父节点的右孩子,则继续找父节点,直到它不是右孩子或父节点为空,第一个非右孩子节点的父亲节点就是后继节点,如果父节点为空,则后继节点为null。
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) { // 如果有右节点,获取右节点的最左节点,因为右节点大于父节点,左节点小于父节点
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else { // 没有右子节点,查询祖先节点
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
节点删除
经过后继节点的替换后,要删除的节点有两种情况,我们约定,删除的节点为N,子节点为X1,它的父节点为P。
情况一、有一个子节点
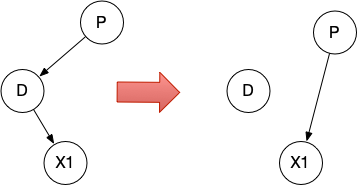
...
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
...
}
...
情况二、无子节点
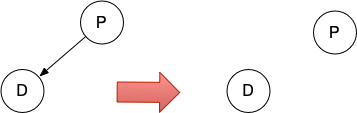
...
} else { // No children. Use self as phantom replacement and unlink.
...
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
...
再平衡
节点删除后,可能破坏原有树的平衡,所以我们需要对树做再平衡处理。在做再平衡处理之前,我们先回顾一下红黑树的5个规则,这5个规则非常重要:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
我们对上面的两种情况再细分处理。
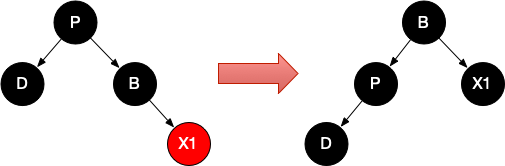
情况一、有一个子节点
情况1.1、D为红色
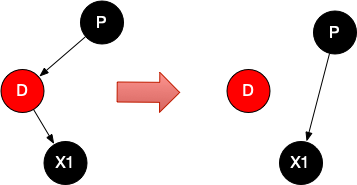
情况1.2、D为黑色
此时,D的子节点X1必为红色,否则违反黑节点数原则(规则5)。
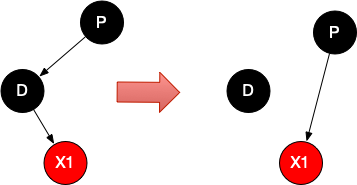
...
if (p.color == BLACK)
fixAfterDeletion(replacement);
...
这里的p即为我们的D节点,replacement即为我们的X1节点。
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
...
}
setColor(x, BLACK);
}
此时,只需将X1节点变成黑色即可。
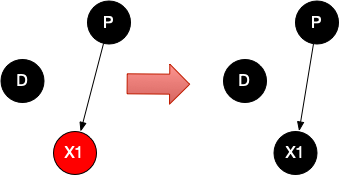
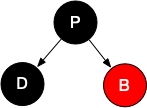
情况二、无子节点
我们约定D的兄弟节点为B,B的两个子节点为X1、X2。
情况2.1、D为红色
不影响树的平衡,直接删除即可,也无需做再平衡处理。
情况2.2、D为黑色,B为红色
此时根据规则4,父节点P一定为黑色,X1、X2一定为黑色
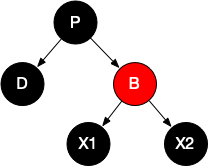
情况2.3、D为黑色,B为黑色,X1、X2为红色
此时P可黑可红。
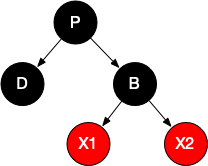
情况2.4、D为黑色,B为黑色,B只有一个左子节点X1,为红色
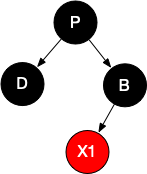
情况2.5、D为黑色,B为黑色,B只有一个右子节点X1,为红色

情况2.6、D为黑色,B为黑色,X1、X2不存在
此时P可黑可红

做再平衡处理时,就是对上述6种情况进行处理,实际是5种,情况2.1忽略掉。处理后有两种结果:
- D节点为红色,树是平衡状态。这时删除D节点,不影响树的平衡。
- D节点为黑色,D节点所在的那条线多一个黑色节点,树不平衡。D被删除后,树自动平衡了。
JDK8中实现
对照着JDK8 TreeMap中fixAfterDeletion的源码
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { // ① 如果x为左子节点
Entry<K,V> sib = rightOf(parentOf(x)); // ② x的兄弟节点
if (colorOf(sib) == RED) { // ③ 情况2.2,转换成情况2.6
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) { // ④ 情况2.6
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) { // ⑤ 情况2.4,转换成情况2.5
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// ⑥ 情况2.3、2.5,转换后的情况2.4
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric ⑦ 对称操作
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
①:先处理x作为左子节点的情况,这里的x相当于我们的D节点。
②:获取x的兄弟节点,这里的sib相当于我们的B节点。
③:情况2.2,转换成情况2.6
④:情况2.6,先将D的兄弟节点变成红色,然后让x指向P,这时P可黑可红,即x可能是黑色,也可能是红色。
(1) 如果x为红色,不满足`colorOf(x) == BLACK`判断条件,退出循环。`setColor(x, BLACK);`,将x变成黑色,这时x所在的那条线比它的兄弟所在的那条线多一个黑色节点,满足上面说的结果2。由情况2.2转换成情况2.6时,x一定为红色。**情况2.2已处理完毕** (2) 如果x为黑色,即情况2.6时P节点为黑色,P为红色时,上面已处理过了。进入下次循环,此时B为红色,进入代码①中
if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateLeft(parentOf(x)); sib = rightOf(parentOf(x)); }处理后结果为
此时 sib就是我们的P节点。 程序继续往下执行,leftOf(sib)就是我们的D节点,所以满足colorOf(leftOf(sib)) == BLACK条件。rightOf(sib)等于P的右节点,此时P的右节点为叶节点(NIL节点),红黑树的规则3(所有叶子都是黑色),所以满足colorOf(rightOf(sib)) == BLACK判断条件。进入代码块④,将P变为红色,之后和上面(1)中一样。情况2.6已处理完毕
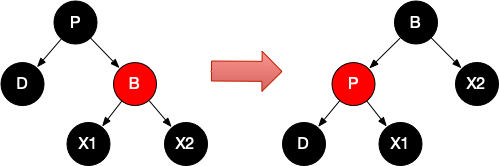
⑤:情况2.4,转换成情况2.5
⑥:情况2.3、2.5,转换后的情况2.4。以情况2.5为例:
之后 x = root,退出循环。D被删除后,树又平衡了。
⑦:当x为右子节点时,和上面一样,做对称操作即可。这里不再赘述。
至此,TreeMap的remove操作完成。
红黑树的删除后再平衡处理,不同的人有不同的处理方法,JDK8只是提供了一种处理方式。不管用什么方法,都是针对上面的情况2.2~情况2.6,最后得到2种结果。