一.什么是熵?
熵是一个物理学上的概念。19世纪,物理学家开始认识到,世界的动力是能量,并且提出"能量守恒定律",即能量的总和是不变的。但是,有一个现象让他们很困惑。物理学家发现,能量无法百分百地转换。比如,蒸汽机使用的是热能,将其转换为推动机器的机械能。这个过程中,总是有一些热能损耗掉,无法完全转变为机械能。一开始,物理学家以为是技术水平不高导致的,但后来发现,技术再进步,也无法将能量损耗降到零。他们就将那些在能量转换过程中浪费掉的、无法再利用的能量称为熵。能量从一种状态转换成另一种状态,这个过程总会产生损耗,能量减少,但是能量的状态增多了,系统变成更混乱了,即产生了熵。
熵是系统混乱程度的度量,越是有序的系统能量越高、熵越低、越不稳定;相反越是无序的系统能量越低、熵越高、越稳定。
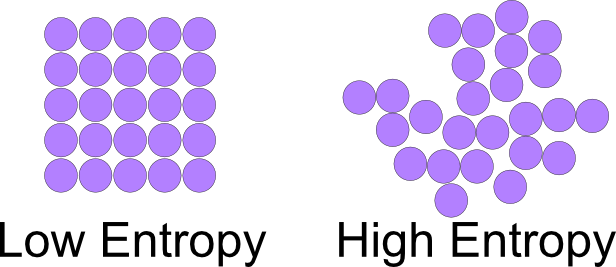
凡是运动的系统都会有能量转换,有能量转换就会有损耗,熵就会增加。宇宙中所有物体都在运动,因此能量最终都会转变成熵,即宇宙万物都处在一种有序趋向无序的状态中。这个概念被称为热力学第二定律,也叫“熵增定律”,即事物总会朝着熵最大化的趋势演变。
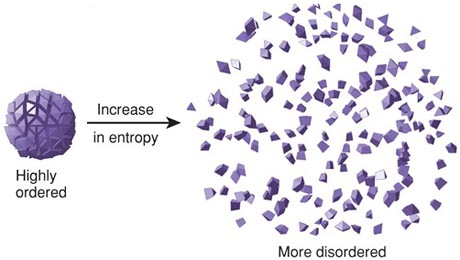
熵也可以理解成系统不做功能力的指标。越是高能物质,越不稳定,越容易发生能量转换,即做功能力越强,相反不做功能力就越弱,即熵越低;当能量发生转换,其做功能力就下降了,相反不做功能力就增强了,即熵增加了。因此熵也是能量退化的指标。
世间万物都在寻求一种平衡,它会朝着越来越稳定的方向演变,这个过程熵一直增加,事物永远向着更混乱的状态发展。比如落红会化作春泥,你我终将化为尘土,沧海变桑田,太阳终有一天将化为星云,整个宇宙达到热平衡,所有地方温度一样,即热寂。
二.信息熵
信息熵是香农参考热力学熵提出的,它代表观察者对某一事件(结果)的未知程度。熵与信息的概念是相对的,信息量度量的是一个具体事件发生了所带来的信息,而熵则是在结果出来之前对可能产生的信息量的期望。获取信息意味着消除不确定性,也就是消除熵,他们的数量是相等的。
获取消息 = 消除熵
信息熵定义,如果一个事件发生的概率是p,则其信息熵为
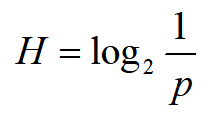
信息熵是编码这个信源平均所需要的最小位数。比如抛三枚硬币,正反的概率都是1/2,那么三枚硬币依次是“正反反”这个事件的信息熵为log(8) = 3,即至少需要3个bit来表示,如100(1代表正面,0代表反面)。
如果各种情况发生的概率不同怎么计算的?例如:变量A有n种可能取值,第i 种的发生概率为p(i),则A的信息熵为每种可能的信息熵的加权平均数
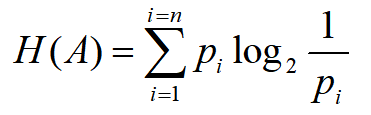
A : 110
B : 10
C : 0
D : 111
根据信息熵定义,这张试卷每道选择题的信息熵为1.75,即每道选择题的平均编码长度为1.75
1/8 * 3 + 1/4 * 2 + 1/2 * 1 + 1/8 * 3 = 1.75
整张试卷的传输数据量为:
25 * 3 + 50 * 2 + 100 * 1 + 25 * 3 = 350
平均每道题的传输数据为 350 / 200 = 1.75bit,刚好等于最小编码位数,说明我们采用的编码方法是最优的,无法再压缩了。
三.熵编码
香农提出了信源编码定理。该定理说明了香农熵与信源符号概率之间的关系,说明信息的熵为信源无损编码后的平均码字长度的下限。任何的无损编码方法都不可能使编码后的平均码长小于香农熵,只能使其尽量接近。基于此,对信源进行熵编码的基本思想,是使其前后的码字之间尽量更加随机,尽量减小前后的相关性,更加接近其信源的香农熵。这样在表示同样的信息量时所用的数据长度更短。
通俗来讲,信息熵描述表示某个信息的最小平均码长;而熵编码的目的就是优化编码方式,让平均码长尽量接近信息熵。
常见的熵编码有:
- 哈夫曼编码
- 算数编码
- 游程编码
3.1 哈夫曼编码
我们直接通过一个例子来了解哈夫曼编码。例如我们要发送一份电报“AAAAAAAAAABBBBCCCDDE”,共20个字母,A-10个,B-4个,C-3个,D-2个,E-1个。哈夫曼编码步骤为:
- 每次找出概率最小的两个字母,以这两个字母为左右子节点,生成父节点,父节点的新节点概率为他们的概率之和,给左右路径加上0、1编码(父节点后面会替代其下的所有子节点参与都查找过程中)
- 一直重复上述步骤直到生成根节点
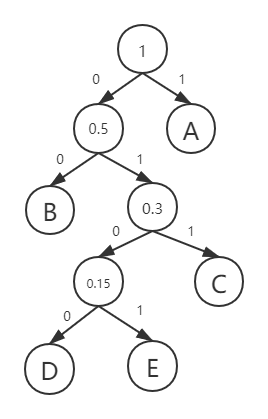
通过上图我们可以得到ABCDE的编码
| 字母 | 概率 | 编码 | 字节长度 | 信息熵(log2(1/p)) |
|---|---|---|---|---|
| A | 0.5 | 1 | 1 | 1 |
| B | 0.2 | 00 | 2 | 2.32 |
| C | 0.15 | 011 | 3 | 2.73 |
| D | 0.1 | 0100 | 4 | 3.32 |
| E | 0.05 | 0101 | 4 | 4.32 |
我们将电报内容转换成二进制编码“111111111100000000011011011010001000101”,与此同时我们还需要将码表一起发送过去,这样对方收到这些二进制编码,对照码表就能将二进制数据还原成原始报文。
观察上表,我们发现哈夫曼编码并不能保证每个节点都等于信息熵的长度;另外观察ABCDE的编码可以看出,他们开头都不一样,其中任意一个编码都不能以其他编码开头,这样才能保证信息的准确性(没有歧义)。传输数据长度为39:
1 * 10 + 2 * 4 + 3 * 3 + 4 * 2 + 4 * 1 = 39
平均码长为 39 / 20 = 1.95,而信息熵为1.92
0.5 * 1 + 0.2 * 2.32 + 0.15 * 2.73 + 0.1 * 3.32 + 0.05 * 4.32 = 1.92
可见哈夫曼编码并不能保证达到最优编码。
哈夫曼编码的优点是压缩很高,缺点也很明显,它需要事先知道所有信息出现的概率,才能开始进行编码,这势必会增加消息处理的延迟,因此很多对实时性要求比较高的场景不会采用哈夫曼编码,比如视频压缩。另外哈夫曼编码还需要传输码表,这也增加了传输负担,某些极端的场景下码表信息非常大,用哈夫曼编码反而得不偿失。