5分钟带你领略：写一个二分查找为什么让面试者挂的这么惨？

二分查找可以说是所有算法中最基础、最容易理解的算法之一了，但事实上也是挂科率最高的考题之一，在各个大厂的应届生面试中，这样的评价屡见不鲜: 谈项目的时候来聊的好好的，叫他写个二分搜索却写不出来。对此我不做评论，就二分查找而言，我觉得它并没有大家想象那样容易，用“思路很简单，细节是魔鬼”来形容最贴切不过了，不信咱们来一步步瞧一瞧。

难点一: 边界判断

二分查找代码大致如下:

let binarySearch = (arr, target) => {
    let begin = 0;
    let end = ???;
    while(???) {
        int mid = begin + (end -begin) / 2;
        if(arr[mid] == target) {}
        else if(arr[mid] > target) {}
        else if(arr[mid] < target) {}
    }
    return ???;
}

可以看到，问题已经很明显了，很多人没有准备的情况下，基本的框架能够写出来，但是边界条件一直搞不清楚，导致情绪紧张、思维错乱，最后不了了之。

现在就来拆解一下各种边界条件，

let search = (arr, target) => {
    let begin = 0;
    let end = arr.length-1; //写成这样，相当于搜索区间为[begin, end]，这是一个闭区间
    while(begin <= end) {//重点: 因为闭区间，所以到了begin等于end时，其实区间内还有一个值要判断，
                         //因此只有begin>end的时候才能停止
        let mid = (begin + end) >>> 1;//位运算，无符号右移一位，同Math.floor((begin+end)/2)
        if(arr[mid] == target) {
            return mid;
        }
        else if(arr[mid] > target) {
            end = mid - 1;//因为是闭区间，搜索范围变为[left, mid - 1]
        }
        else if(arr[mid] < target) {
            begin = mid + 1; //搜索范围变成[mid + 1, end]
        }
    }
    return -1;
}

其实我们也可以这么来做:

let search = (arr, target) => {
    let begin = 0;
    let end = arr.length; //写成这样，相当于搜索区间为[begin, end)，这是一个前闭后开的区间
    while(begin < end) {//重点:
                       //因为前闭后开的区间，所以到了begin等于end时，其实区间内已经没有值了，直接停止
        let mid = (begin + end) >>> 1;
        if(arr[mid] == target) {
            return mid;
        }
        else if(arr[mid] > target) {
            end = mid;//因为是闭区间，搜索范围变为[left, mid - 1]
        }
        else if(arr[mid] < target) {
            begin = mid + 1; //搜索范围变成[mid + 1, end]
        }
    }
    return -1;
}

我想注释已经解释的足够清楚了，希望大家能够理解区间判断的原理，而不是去一味的背代码。

顺便提一下，根据上面的思路，我们也可以写成递归的方式:

let search = (nums, target) => {
    let helpSearch = (nums, begin, end, target) => {
      if(begin > end) return -1;
      let mid = (begin + end) >>> 1;
      if(nums[mid] == target) return mid;
      else if(nums[mid] > target) 
        return helpSearch(nums, begin, mid - 1, target);
      else 
        return helpSearch(nums, mid+1, end, target);
    }
    //闭区间形式
    return helpSearch(nums, 0,  nums.length - 1, target);
}

let search = (nums, target) => {
    let helpSearch = (nums, begin, end, target) => {
      if(begin >= end) return -1;
      let mid = (begin + end) >>> 1;
      if(nums[mid] == target) return mid;
      else if(nums[mid] > target) 
        return helpSearch(nums, begin, mid, target);
      else 
        return helpSearch(nums, mid+1, end, target);
    }
    //前闭后开区间形式
    return helpSearch(nums, 0,  nums.length, target);
}

难点二: 目标值重复的情况

直接看一道真题吧:

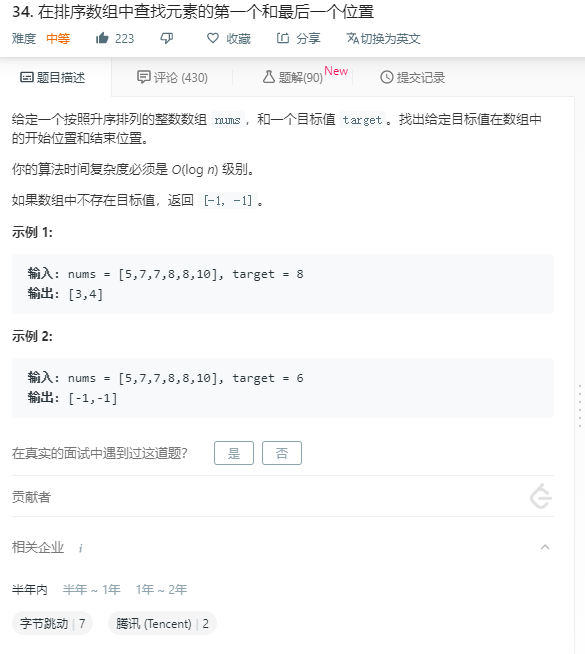
O(log n)级别的时间复杂度，说白了就是二分查找，也就是说，我们需要用二分查找的方式找到目标值最左边的位置和最右边的位置, 其实还是有一些复杂的。

接下来让我们分步骤拆解。

寻找左边界位置

let left = 0;
let mid;
let right = nums.length;
while(left < right) {
  mid = (left + right) >>> 1;
  if (nums[mid] > target) {
      right = mid;
  } else if (nums[mid] < target) {
      left = mid + 1;
  } else if (nums[mid] == target) {
      right = mid; //重点
  }
}
//分析:目前的nums[left]一定是大于等于target的值
if (left == nums.length) return -1;
else return nums[left] == target ? left : -1;

寻找右边界位置

let left = 0; 
let right = nums.length;
while(left < right) {
  mid = (left + right) >>> 1;
  if (nums[mid] > target) {
      right = mid;
  } else if (nums[mid] < target) {
      left = mid + 1;
  } else if (nums[mid] == target) {
      left = mid + 1; //注意
  }
}
//分析: 目前的nums[left]左边的部分都是大于等于target的部分，因此我们取nums[left - 1]
if (left == 0) return -1;
else return nums[left - 1] == target ? left - 1: -1;

当然我这里都是用的前闭后开的区间，你也可以直接用闭区间完成。

最后代码展示

var searchRange = function(nums, target) {
  let left = 0;
  let mid;
  let right = nums.length;
  while(left < right) {
      mid = (left + right) >>> 1;
      if (nums[mid] > target) {
          right = mid;
      } else if (nums[mid] < target) {
          left = mid + 1;
      } else if (nums[mid] == target) {
          right = mid;
      }
  }
  let leftIndex = -1, rightIndex = -1;
  if (left == nums.length) return [-1, -1];
  else leftIndex = nums[left] == target ? left : -1;

  left = 0; right = nums.length;
  while(left < right) {
      mid = (left + right) >>> 1;
      if (nums[mid] > target) {
          right = mid;
      } else if (nums[mid] < target) {
          left = mid + 1;
      } else if (nums[mid] == target) {
          left = mid + 1;
      }
  }
  if (left == 0) return [-1, -1];
  else rightIndex = nums[left - 1] == target ? left - 1: -1;
  
  return [leftIndex, rightIndex];
};

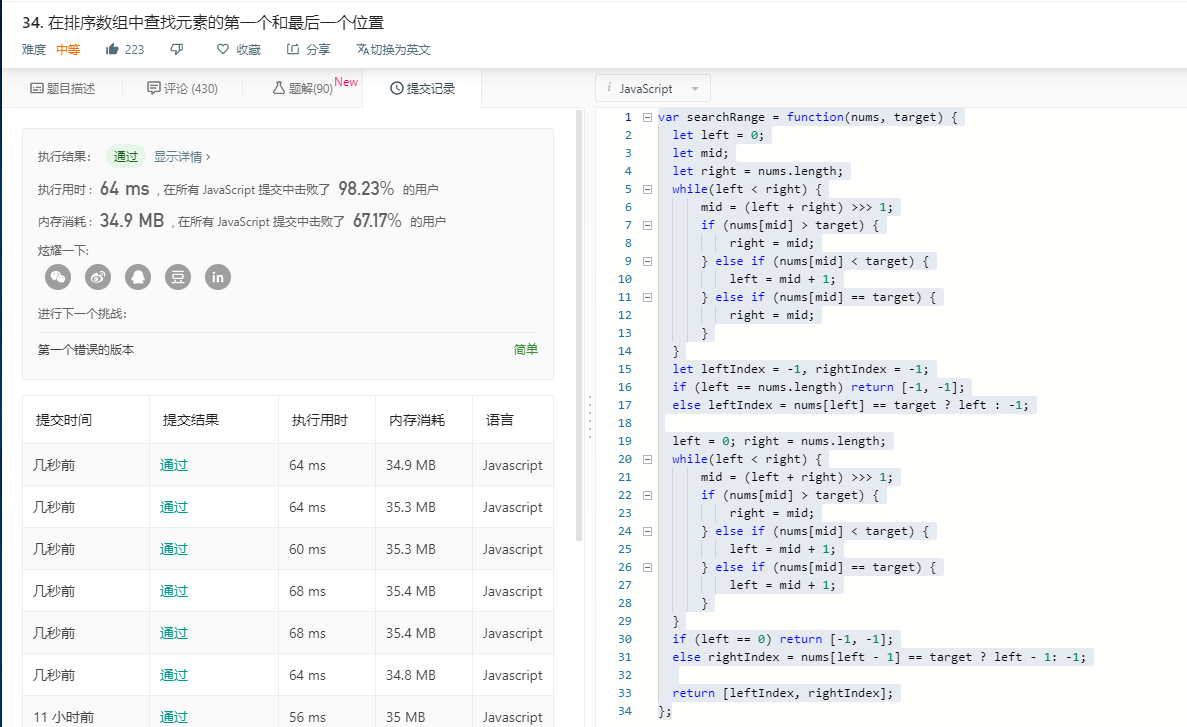
总而言之，二分搜索思维难度确实不大，但是要将边界变量代表的区间含义理解的非常清楚，这样才不至于思维紊乱，细节考虑清楚了，各种不同的方法便可以来去自如了。