数据工程师惯用python,然而数据结构还是c++或者java比较经典。这就造成很多朋友并不太习惯。本文就从《剑指offer》这本书中的经典题型出发,来研究探讨一下python 刷数据结构题型的一些惯用思路。
可能有过几年编程经验的朋友们对于一些常用的程序了如指掌,却总是觉得二叉树,链表,堆栈这些略微遥远。但是想要进阶却不得不跨过这道坎。那么本文重点研究一下二叉树的一些常用思路。
二叉树介绍
二叉树,通俗一点来说就是至多有两个子结点的树结构。结构并不复杂,但是为什么要使用这样一个结构呢?简单来比较一下在此之前的一些数据基本结构。
- 数组:最原始的数据结构之一了,其优点在于查找的复杂度为
,然而想插入删除某一数据,就需要将插入点或删除点之后的数据全部移位操作,复杂度为
- 链表:数据像链条一样串起来,前一个结点包含后一个结点的指针。这样访问第一个就可以按照指针一路遍历到最后。其优势在于插入删除复杂度为
,因为只需要更换一个结点的指针指向就可以实现插入删除了。但其查找的复杂度为
,因为要遍历才可以查找。
- 二叉树:二叉树是将所有数据放在一个树形结构中,一个d层的二叉树可以储存的数据为(N =
)个数据,其查找和插入删除复杂度都为
,算是对数组和链表的一种折中考虑。
二叉树的储存
计算机内部的储存一直没有算法更加受人瞩目,因为我们可以将其当作黑盒来使用。但是我这里要提一句,因为刷题的时候会有测试样例,如果我们不知道二叉树是如何存在数据里的,就不可理解测试样例是什么意思。
-
顺序储存:将二叉树逐层从左至右自上而下遍历,如果不是完全二叉树,有残缺结点的话就补上‘#’。我们来看下面这张图:
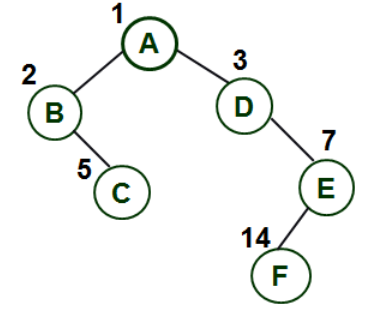
"ABD#C#E######F",值得注意的是,由于F为最后一个结点了,所以其后的空结点并不写出来。 -
链表式储存:将二叉树按照链表的形式储存起来。这是最常用的储存方法。在这种储存方法中,二叉树和链表一样,是一种python的对象。对象内包括左子结点的指针,右子结点的指针,还有自己所代表的数值。我们常用的定义链表式二叉树代码:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
二叉树的遍历
遍历指的是我们访问且不重复访问二叉树的所有结点。一般常用的有三种:前序遍历,中序遍历和后序遍历。简单介绍下:
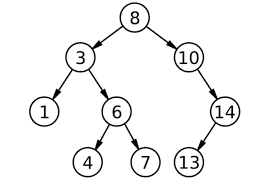
- 前序遍历:先访问根节点,再访问左子结点,最后访问右子节点。上图的前序遍历为【8,3,1,6,4,7,10,14,13】
- 中序遍历:先访问左子结点,再访问根节点,最后访问右子结点。上图的中序遍历为【1,3,4,6,7,8,10,14,13】
- 后序遍历:先访问左子结点,再访问右子节点,最后访问根节点。上图的后序遍历为【1,4,7,6,3,13,14,10,8】对于后序遍历,注意根节点的左子树遍历完之后再去遍历右子树。
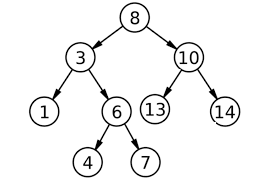
也可知,我们通过某一给定的二叉树,可以得到唯一的前,中,后序遍历序列,但是反之,我们只有三种遍历序列中的一个时,并不能恢复成唯一的二叉树,想要恢复,至少需要关于改二叉树的两个遍历序列。举个例子,只给定上图的后序遍历也可以恢复成这样:
二叉树的几种特殊形式
- 二叉搜索树:是二叉树的一种特例。其特点就是左子结点的值小于等于根节点,而右子结点的值大于等于根节点值。这样排列的好处,就是我们可以在
时间内搜索到任意结点。
- 二叉平衡树(AVL):父节点的左子树和右子树的高度之差不能大于1,也就是说不能高过1层。我们构想这样一个二叉树,左子结点完全没有,只有右子节点有N的深度。那么此时二叉树其实就是一个链表,查找复杂度依旧是
。这时我们会发现,一般的二叉树搜索复杂度并不可以到
。只是在完全树的状态下,我们才可以达到这样的性能。平衡二叉树就是为了缓解这左右子树深度差距过大而产生的。
开始刷题
重建二叉树
题目内容:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思考:由前文可知,只知道前,中,后序遍历中的某一种我们是无法恢复唯一的二叉树的。而对于已知两种遍历,我们可以逐步分析出二叉树的各种细节。
我们分析前序序列,前序序列的第一个数字是根节点的值,而中序序列根节点在序列中间。
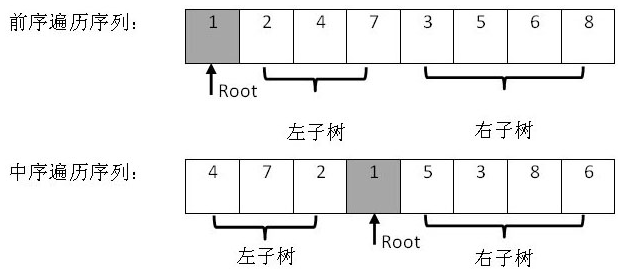
如上图,根据root结点我们可以分出左右子树。则对左右子树重复以上操作,便可得到最终的二叉树结构。这里我们有重复某一操作的操作,针对这种情况,我们常用递归方法。
递归法重建二叉树
# -*- coding:utf-8 -*-
# 被注释的代码表示了系统构建链表式二叉树
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 这里定义函数,两个参数分别是前序和中序遍历的序列,两个数组
def reConstructBinaryTree(self, pre, tin):
# 以下两个if是为了判断一下特殊情况
# 但是其最重要的作用其实是整个函数的终止条件
# 因为递归调用,函数嵌套着函数,在运行第一遍函数的时候是不能直接得到结果的
# 递归过程中,子树被不断细化,直到长度为1或者0的时候,通过这两个if得到答案
# 然后从嵌套中一个一个解开,使得整个递归过程得到最终解并且终止
if len(pre) == 0:
return None
if len(pre) == 1:
return TreeNode(pre[0])
else:
root = tin.index(pre[0]) # 按照前序遍历找到中序遍历的root结点
res = TreeNode(pre[0]) # 利用TreeNode类来将这个数组中的root结点初始化成二叉树结点
res.left = self.reConstructBinaryTree(pre[1: root + 1], tin[: root])
# 递归调用此函数,不断细化子树,直到遍历到最后一个结点,那么递归过程的
# 每一个结点会相应解开
res.right = self.reConstructBinaryTree(pre[root + 1: ], tin[root + 1: ])
return res
二叉树的子结构
题目描述:输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)如图,第二棵树为第一棵树的子树。
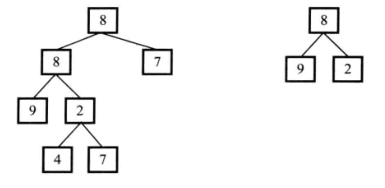
思考:我们是要判断B是不是A的子结构,则B是子树,A为原树。我们可以先找到B的根结点在A树中的位置,然后再看A中该节点之下有没有与B树结构一样的子树。那么这道题就被拆解成两个比较简单的子题目。
- 那么我们分为两步,我们首先是要再A中找到B的根结点。
def HasSubtree(self, pRoot1, pRoot2):
# 判断一下特殊情况
if pRoot1 == None or pRoot2 == None:
return False
result = False
# 此为递归终止条件,函数沿着树去寻找,直到符合此条件才返回值。
# 找到了就返回此结点,注意A和B的地位不一样,所以返回pRoot1和pRoot2可以考虑下
if pRoot1.val == pRoot2.val:
result = self.isSubtree(pRoot1, pRoot2)
if result == False:
# 没找到的话,就向左子结点重复以上过程
result = self.HasSubtree(pRoot1.left, pRoot2)
if result == False:
# 左子结点还没有才找右边的。可以感受一下这个顺序
result = self.HasSubtree(pRoot1.right, pRoot2)
return result
- 找到根节点,就开始看结点之下是否有与B相同的结构树
def isSubtree(self, pRoot1, pRoot2):
# 这里我们要注意,由于B是子,A是原,所以这两个地位不一样
# 区别可以体现在Root1和Root2两个结点的判断上,具体看以下两个if
if pRoot2 is None:
return True
if pRoot1 is None:
return False
if pRoot1.val != pRoot2.val:
return False
# 注意此条,两个都为真,才返回真。
return self.isSubtree(pRoot1.left, pRoot2.left) and self.isSubtree(pRoot1.right, pRoot2.right)
对这两个部分都熟悉之后,我们只需要拼起来就可以了。以下为完整代码。
递归法判断二叉树的子结构
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def HasSubtree(self, pRoot1, pRoot2):
# write code here
if pRoot1 == None or pRoot2 == None:
return False
result = False
if pRoot1.val == pRoot2.val:
result = self.isSubtree(pRoot1, pRoot2)
if result == False:
result = self.HasSubtree(pRoot1.left, pRoot2)
if result == False:
result = self.HasSubtree(pRoot1.right, pRoot2)
return result
def isSubtree(self, pRoot1, pRoot2):
if pRoot2 is None:
return True
if pRoot1 is None:
return False
if pRoot1.val != pRoot2.val:
return False
return self.isSubtree(pRoot1.left, pRoot2.left) and self.isSubtree(pRoot1.right, pRoot2.right)
二叉树的镜像
题目描述:操作给定的二叉树,将其变换为源二叉树的镜像。
源二叉树
8
/ \
6 10
/ \ / \
5 7 9 11
镜像二叉树
8
/ \
10 6
/ \ / \
11 9 7 5
思考:看着官方给的镜像实例,我们可知,只需要将根节点下的每一个左右子树都调换一下就ok。那也同样的,我们使用递归,遍历到所有结点,并对其调换左右子结点。这里我们要注意到可能有左右子结点不完全的问题,不过没有关系,空结点也可以调换的。所以只需考虑root结点是否为空这一个特殊条件就可以了。
二叉树的镜像
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回镜像树的根节点
def Mirror(self, root):
if root == None:
return None
# python的调换语句倒不需要c那种的temp
# 其实最标准的这里应该加上判断如果left和right是否有值,
# 但是同样的,空结点也可以调换,所以只考虑根节点是否为空。
root.left, root.right = root.right, root.left
if root.left:
# 对每个子结点还进行同样的递归操作便好
self.Mirror(root.left)
if root.right:
self.Mirror(root.right)
从上往下打印二叉树
题目描述:从上往下打印出二叉树的每个节点,同层节点从左至右打印。
思考:这道题其实跟我们二叉树的顺序储存很类似,可以看作是二叉树的链表储存对顺序储存方式的转化吧。如下图所示,我们打印出来的为【A,B,C,D,E,F,G】,我们先从根节点开始,接下来打印根节点的两个子结点,第三步得从第二层的每个子结开始,分别打印每一个子结点的左右子结点,如此循环。这里我们很容易看出,我们得保存每一层的所有结点,作为下一次遍历时候使用。
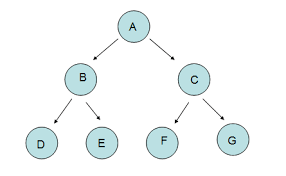
循环实现从上往下打印二叉树
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def PrintFromTopToBottom(self, root):
# write code here
if not root:
return []
list = [] # list 作为最终遍历结果保存的数组
level = [root] # level作为保存每层root结点的数组
while level:
newlevel = []
for i in level:
if i.left:
newlevel.append(i.left)
if i.right:
newlevel.append(i.right)
list.append(i.val)
level = newlevel
# 我们会发现level所表示的比list要更早一层
return list
这里很多网上教程使用队列,可能有些不太熟悉的朋友觉得很高级。其实很简单,就一直将上一层的结点弹出栈之后再将下一层的压入栈,跟我们这种将数组置空再添下一层的做法其实异曲同工。
这一题用循环简洁明了。递归调用的话理解略微繁琐。因为递归调用很容易向深处遍历,而非在一个层。这就不太适合这道题的解法。当然,循环与递归本是同根生,我写下递归的方法给大家参考一下。
思路是这样:递归方法虽然喜欢向深处遍历,但是我们给每个结点都打上深度的标签,然后用二维数组将这些带深度标签的按深度归类,是不是就可以解决了。
递归法打印二叉树
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回从上到下每个节点值列表,例:[1,2,3]
def __init__(self):
self.res = list()
def Traversal(self, node, depth=0):
if not node:
return True
# 我们这里设置一个depth的概念,代表树的深度。这里我们可知,根节点是第1层,但是depth = 0
# 所以发现depth总是小于len(self.res)的。一旦这两者相等,我们便可知,上一层已经满了,这个depth代表的是新的一层
# 我们就需要在self.res中开一个新的数组了
if len(self.res) == depth:
self.res.append([node.val])
else:
self.res[depth].append(node.val)
# 我们这里return的值是一个boolean类型的,但是我们不用去管这个具体是什么。我们需要的是self.res
# 这里传参的时候相当于给每个结点都附上了depth值。
return self.Traversal(node.left, depth+1) and self.Traversal(node.right, depth+1)
def PrintFromTopToBottom(self, root):
# 我们调用一下这个Traversal函数便可得到我们的最终序列,
# 但是这个序列里面每个元素都是一层数值的list,所以还得拆解一下
self.Traversal(root)
list = []
for level in self.res:
for num in level:
list.append(num)
return list
之字形打印二叉树
题目描述:请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。如图之字形遍历为【A,B,C,F,E,D】
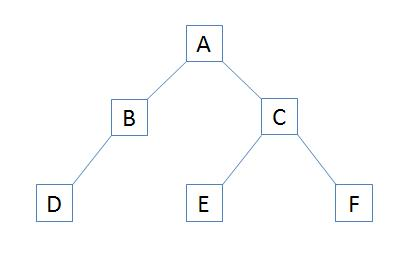
思考:这题有上面的题作为基础,就很容易了。遍历好之后将奇数层反转一下就可以。
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def Print(self, pRoot):
res = list()
def Traversal(node, depth=0):
if not node:
return True
if len(res) == depth:
res.append([node.val])
else:
res[depth].append(node.val)
return Traversal(node.left, depth+1) and Traversal(node.right, depth+1)
Traversal(pRoot)
# 上面那部分和打印二叉树题目是一样的,接下来进行一个判断奇数层取反转的操作
for i, v in enumerate(res):
if i % 2 == 1:
v.reverse()
return res
二叉树的深度
题目描述:输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
思考:由之前的打印二叉树,我们可以渐渐感觉到递归调用对于二叉树来说,很容易向深处遍历。意思就是递归函数的嵌套,只会沿着指针前进的方向,而指针一直指向更深层的树中去。那么这一题求深度,就将递归的优势展现的淋漓尽致了。
那我们就将每一个分支都给遍历到,求最深的即可。我们递归可以做到,对于每一个结点,都给判断一下左右结点所处深度,然后返回最大的。而循环在这一题中,很容易有重复冗余的操作,劣势显现。我们后续可以比较一下。
递归求二叉树深度
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def TreeDepth(self, pRoot):
if pRoot == None:
return 0
# 这里只管遍历
ldepth = self.TreeDepth(pRoot.left)
rdepth = self.TreeDepth(pRoot.right)
# 深度+1的操作在return时候实现,每次遍历的时候都取一下左右节点最深的那个
# 注意初始的状态,防止算出的值少了一层。
return max(ldepth, rdepth) + 1
递归方法十分简洁,与之比较的是循环法。循环的思路是这样子的。我和打印二叉树一样,将二叉树的每一层都存在数组里。然后看遍历完以后数组中有多少层,那就是二叉树的深度。代码如下:
循环法求二叉树深度
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 层次遍历
def levelOrder(self, root):
# 存储最后层次遍历的结果
res = [] # 层数
count = 0 # 如果根节点为空,则返回空列表
if root is None:
return count
q = [] # 模拟一个队列储存节点
q.append(root) # 首先将根节点入队
while len(q) != 0: # 列表为空时,循环终止
tmp = [] # 使用列表存储同层节点
length = len(q) # 记录同层节点的个数
for i in range(length):
r = q.pop(0) # 将同层节点依次出队
if r.left is not None:
q.append(r.left) # 非空左孩子入队
if r.right is not None:
q.append(r.right) # 非空右孩子入队
tmp.append(r.val)
if tmp:
count += 1 # 统计层数
res.append(tmp)
return count
def TreeDepth(self, pRoot):
# 使用层次遍历 当树为空直接返回0
if pRoot is None:
return 0
count = self.levelOrder(pRoot)
return count
这里我使用的是队列,层次遍历,原理是每开始遍历下一层时都将上一层的结点弹出栈,将下一层的结点压入栈。我们也可以使用之前的每一层置空,然后重新添加结点的方法来做。
当然,两种方法,孰优孰劣一眼便知。
递归和循环,在一般情况下都是可以转化使用的。也就是递归可以用循环来代替,反之亦然。只是两者写法可能复杂性天壤之别。我们通过这两道题可以感受一下。什么时候递归好用,什么时候循环好用,心里得有感觉。
平衡二叉树
题目要求:输入一棵二叉树,判断该二叉树是否是平衡二叉树。(平衡二叉树的定义见上文基础部分)
思考:我们由平衡二叉树的定义可知,我们如果知道左右子结点分别的深度就好办了。相差不大于1,判断一下就可以解决。
平衡二叉树
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 定义这个函数是为了求出子结点以下的深度
def TreeDepth(self, pRoot):
if pRoot == None:
return 0
ldepth = self.TreeDepth(pRoot.left)
rdepth = self.TreeDepth(pRoot.right)
return max(ldepth, rdepth) + 1
def IsBalanced_Solution(self, pRoot):
# write code here
if pRoot == None:
return True
# 求一下两边的深度
ldepth = self.TreeDepth(pRoot.left)
rdepth = self.TreeDepth(pRoot.right)
# 判断一下深度差
if ldepth-rdepth>1 or rdepth-ldepth>1:
return False
else:
# 继续往下遍历
return self.IsBalanced_Solution(pRoot.left) and self.IsBalanced_Solution(pRoot.right)
二叉搜索树的后序遍历序列
题目描述:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
思考:后序遍历中,最后一个数字是根结点的值,数组的前面数字部分可分为两部分,一部分是左子树,一部分是右子树。我们根据二叉搜索树的性质可知,左子树的值要比根节点小,而右子树所有值要比根节点大。以此递归来判断所有子树。
二叉搜索树的后序遍历序列
# -*- coding:utf-8 -*-
class Solution:
def VerifySquenceOfBST(self, sequence):
# write code here
if not sequence:
return False
else:
return self.verify(sequence)
def verify(self, sequence):
if not sequence:
return True
# 根节点就是最后一个树,获取一下这个值,然后从数组中弹出去
root = sequence.pop()
# 找一下左右子树
index = self.findIndex(sequence, root)
# 细分到没有子结点作为终止条件
if not sequence[index:]:
return True
# 如果右边数组最小值都大于root,则说明没有问题。进一步细分
elif min(sequence[index:]) > root:
left = sequence[:index]
right = sequence[index:]
return self.verify(left) and self.verify(right)
return False
# 定义一个函数,来找到左右子树的分界线
# 左子树的值比根节点小,右子树的值比根节点大,以此为左右子树的界限
def findIndex(self, sequence, root):
for i, seq in enumerate(sequence):
if sequence[i]>root:
return i
return len(sequence)
二叉树和为某一值的路径
题目描述:输入一颗二叉树的跟节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
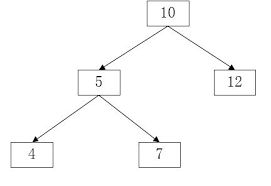
二叉树和为某一固定值的路径
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回二维列表,内部每个列表表示找到的路径
def __init__(self):
# 这里我们定义两个列表。
# list代表的是遍历过程中结点的储存情况,这里面结点随时有变化,但不一定符合要求
# wholelist代表的是最后符合要求的路径储存的列表
self.list = []
self.wholeList = []
def FindPath(self, root, expectNumber):
if root == None:
return self.wholeList
# 将结点值加进来,目标值随着结点值递减
self.list.append(root.val)
expectNumber = expectNumber - root.val
if expectNumber == 0 and root.left == None and root.right == None:
newList = [] # newlist表达的是在遍历过程中符合要求的一条路径,要被加进wholelist里面
for i in self.list:
newList.append(i)
# 这里不直接加self.list,
self.wholeList.append(newList)
# 向左右子结点遍历
self.FindPath(root.left, expectNumber)
self.FindPath(root.right, expectNumber)
# 这里就是不符合要求的了,返回父节点之前,删除当前结点。
self.list.pop()
return self.wholeList
对称二叉树
题目描述:请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。

对称二叉树
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetrical(self, pRoot):
# write code here
if pRoot == None:
return True
return self.isSym(pRoot.left, pRoot.right)
def isSym(self,left,right):
if left == None and right == None:
return True
if left == None or right == None:
return False
# 重点就在这里,判断左右是否一致
if left.val == right.val:
# 一致的话返回 左的左 和 右的右 和 左的右 与 右的左
return self.isSym(left.left, right.right) and self.isSym(left.right, right.left)