二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:(来自 维基百科)
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
节点类
@Data
private class Node {
private E e;
private Node left, right;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
}
二叉查找树基本结构
public class BST<E extends Comparable<E>> {
private Node root;
private int size;
public BST() {
this.root = null;
this.size = 0;
}
}
添加操作
public void add(E e) {
if (e == null) {
return;
}
root = add(root, e);
size++;
}
private Node add(Node node, E e) {
//找到插入位置,创建节点
if (null == node) {
return new Node(e);
}
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
} else if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}
return node;
}
private void addArray(E[] array) {
for (E e : array) {
this.add(e);
}
}
删除操作
public void remove(E e) {
this.remove(root, e);
}
private Node remove(Node node, E e) {
if (node == null) {
return null;
}
//以下两个if在查找要删除的节点在哪
if (e.compareTo(node.e) < 0) {
node.left = remove(node.left, e);
return node;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(node.right, e);
return node;
}
//找到要删除的节点 —> node
else {
//如果要删除的节点的左子树为空,直接返回右子树 -> 即把要删除的节点的右子树 直接放在要删除的节点的位置
if (node.left == null) {
return node.right;
}
//与上同理
else if (node.right == null) {
return node.left;
}
//如果左右子树都存在 -> 找到要删除的节点(node)的右子树中最小节点(即后继节点successor) -> 放在要删除的节点的位置
// -> successor的右子树为原节点的右子树(不过删除了successor) -> successor左子树为原节点的左子树
// -> 原节点左右子树置空
else {
Node successor = min(node.right);
successor.right = deleteMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
}
public Node min(Node node) {
if (node.left == null) {
return node;
}
return this.min(node.left);
}
/**
* 6 6
* / \ -> / \
* 4 7 null 7
*/
private Node deleteMin(Node node) {
if (node.left == null) {
return node.right;
}
node.left = deleteMin(node.left);
return node;
}
查找操作
public Node search(E e) {
return this.search(root, e);
}
private Node search(Node node, E e) {
if (node == null) {
return null;
}
if (e.equals(node.e)) {
return node;
} else if (e.compareTo(node.e) < 0) {
return search(node.left, e);
} else {
return search(node.right, e);
}
}
public Boolean contains(E e) {
return this.search(e) != null;
}
测试
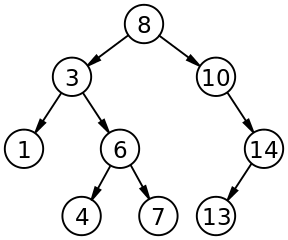
public static void main(String[] args) {
BST bst = new BST();
Integer[] array = {8, 3, 10, 1, 6, 14, 4, 7, 13};
bst.addArray(array);
bst.midOrder();
System.out.println("\n"+bst.search(6));
bst.remove(3);
bst.midOrder();
}
输出:
1 3 4 6 7 8 10 13 14
BST.Node(e=6, left=BST.Node(e=4, left=null, right=null), right=BST.Node(e=7, left=null, right=null))
1 4 6 7 8 10 13 14