空间
从广义上,我们通过宇宙来定义万物,宇宙也是时间和空间的统一。对于整个物理世界,时间和空间是最重要最本质的两个维度。如果抛开时间维度,则可以通过空间来描述事物。空间能容纳事物,就好比现实世界中的人、建筑等都在某个空间内。

数学空间
空间概念也可以推广到其它领域中,比如数学的空间就是点和几何结构的集合。最著名的也是我们平常生活最多接触的就是欧几里得空间,对应着古希腊数学家欧几里得所创建的欧几里得几何。相对于低维度来说主要有平面几何空间和立体几何空间,这些空间中还定义了距离、角、内积一系列概念并规定了相关约束。
如果将二维、三维推广到有限n维,则从二维到有限n维的所有符合定义的空间统称为欧几里得空间。那么主要有哪些定义约束呢?欧几里得空间主要的有五点约束:满足距离的约束、满足线性结构的约束、满足范数的约束、满足内积的约束、必须是有限维度。
向量空间
向量空间对应的对象就是向量,在引入向量概念之后,很多问题的处理都将变得更加简洁清晰。
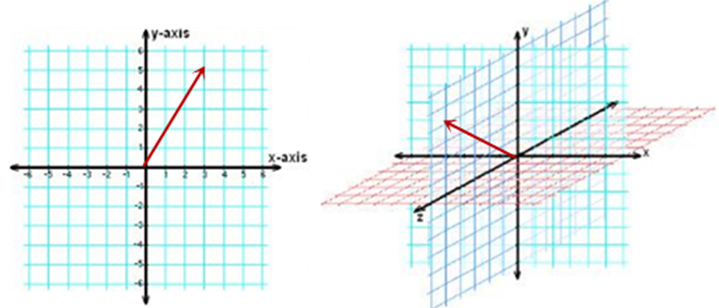
我们能直观感受的向量空间一般为二维和三维的向量空间,也就是对应着平面坐标系(x轴和y轴)和三维坐标(x轴、y轴和z轴)。但实际上,向量空间除了包括二维和三维,同时还能推广到有限n维向量空间。向量空间很重要的是约束就是线性约束,即能够进行加法和数量乘法且满足交换律、结合律、分配律,因此向量空间也叫线性空间。
向量的表示
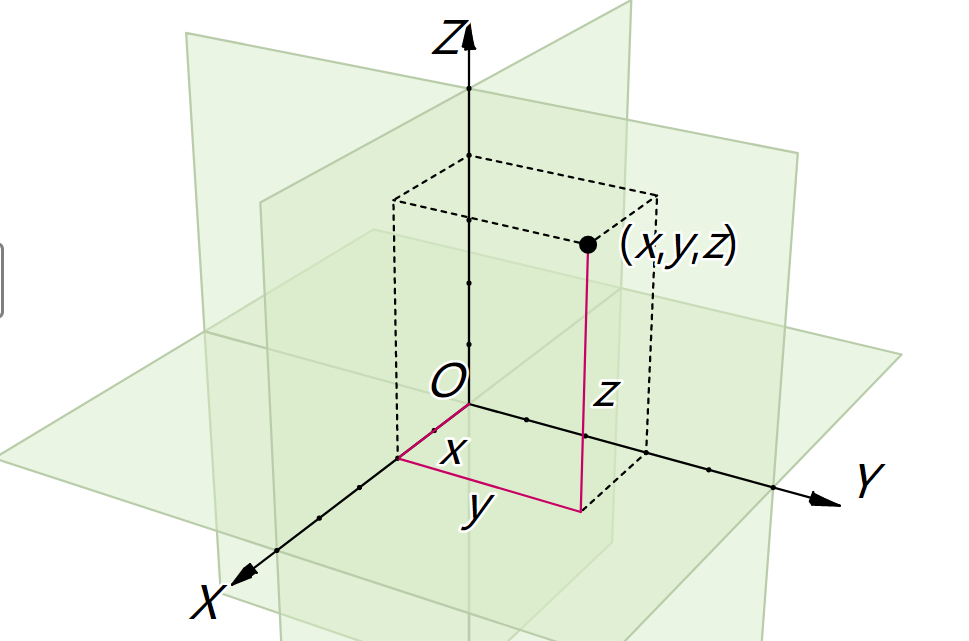
向量是指具有大小和方向的量,可以使用箭头来表示,箭头的长度表示向量的大小,而箭头的方向表示向量的方向。在物理领域,使用矢量作为向量的等同概念,而计算机领域会使用数组或列表来表示向量。如下图中原点(0,0,0)和P点(2,3,5)一起确定了一个向量,该向量可以表示为:
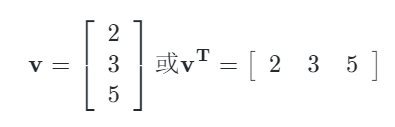
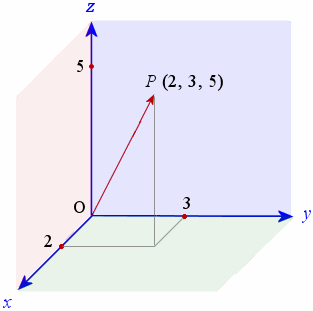
向量抽象万物
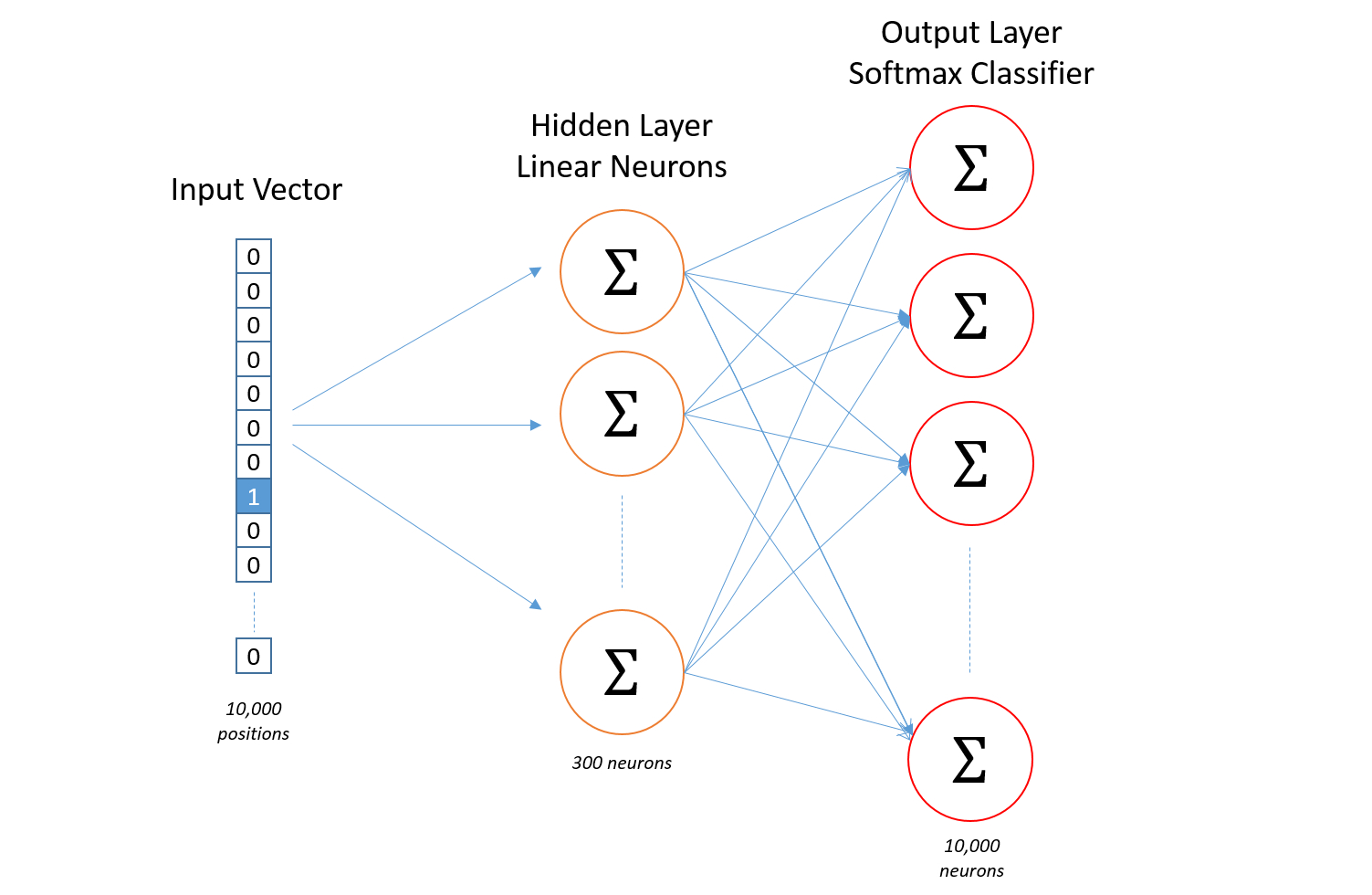
向量在数学上的定义是抽象的,那它有什么作用呢?从更高层面看,向量是一种对事物抽象的思维,同时也是一种很有用的工具,将事物转换到向量体系能高效简洁地解决很多问题。我们可以将事物映射成向量,也可以将事物的特征映射到向量空间。
实际上对于任何事物或特征都可以抽象为向量。将事物表示成向量是模型处理的首要一环,一旦我们将事物抽象成向量后就能够往下建立模型并处理。
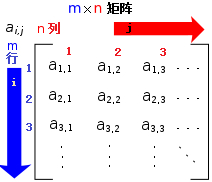
矩阵
矩阵是由m行n列元素组成的矩形阵列,相对于向量,其实可以把矩阵看成是一组向量组成的对象。比如前面的词向量,正是m行1列的特殊矩阵,那么如果指定数量n的单词组成一批,那么就是m行n列矩阵。
对于向量空间来说,矩阵的本质作用就是对向量施加变换操作,也就是说矩阵用来描述变换。比如下面的表达式,向量x经过矩阵A所描述的变换后变为向量y。
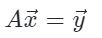
-------------推荐阅读------------
我的开源项目汇总(机器&深度学习、NLP、网络IO、AIML、mysql协议、chatbot)
欢迎关注:人工智能、读书与感想、聊聊数学、分布式、机器学习、深度学习、自然语言处理、算法与数据结构、Java深度、Tomcat内核等相关文章
