树

二叉树是一种树，那树是什么呢

树其实就是不含回路的无向连通图
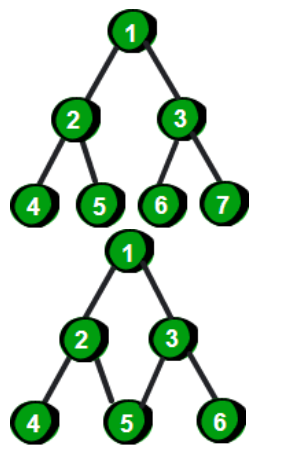
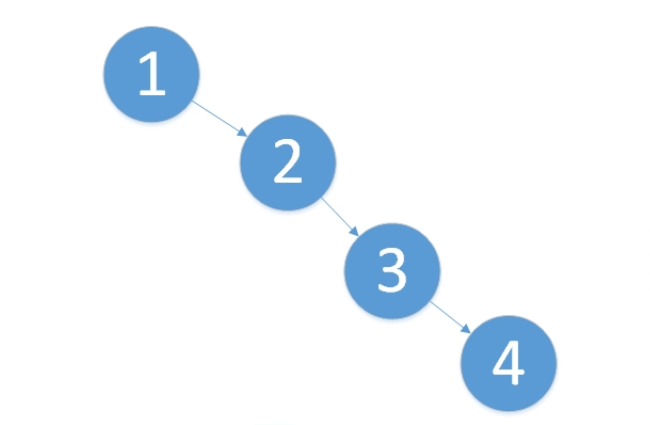
如图，上面那个就是树，与图中下面的有回路的图相比
树的任意两个节点只有一条唯一路径连通

二叉树

二叉树则是一种特殊的树，特点是每个节点至多只有一个左节点和一个右节点，也就是每个父亲节点最多只能有两个儿子节点

完全二叉树

深度为 h的二叉树（深度就是有几层节点），除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层从右向左连续缺若干结点，就是完全二叉树。

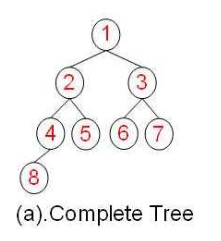
满二叉树

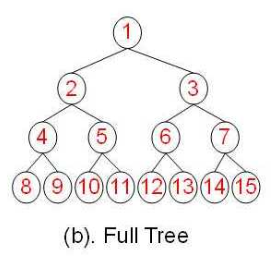
对一个深度为h的二叉树，节点数为2^n-1
也就是每个父亲都完美的生了两个儿子，一家子整整齐齐，是完全二叉树的升级版

二叉查找树

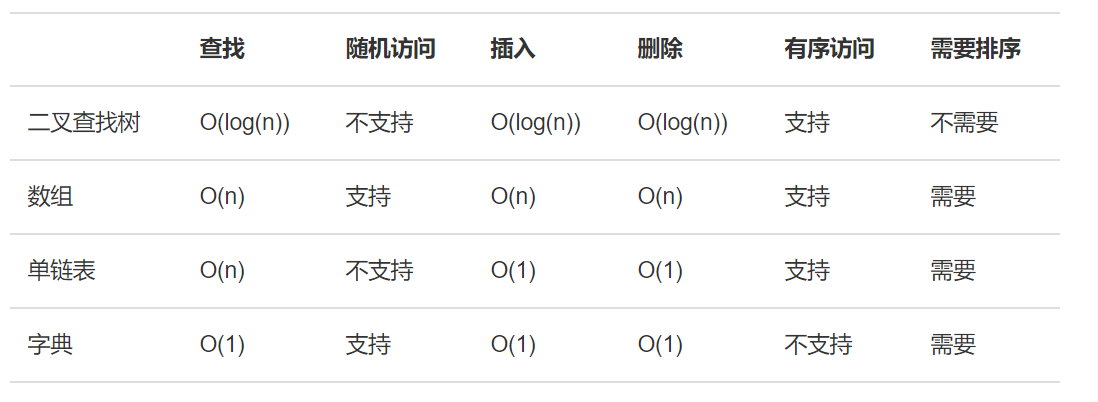
然后便是今天的主角了，二叉查找树（BST）它的规则是：

任意左子树上所有结点的值均小于它的根结点的值
任意右子树上所有结点的值均大于它的根结点的值

之所以要这么规定，就是为了利用二分法的思想，增加查找和插入的效率

平均搜索复杂度为O（logn），已经非常优秀了，不过在最坏的情况下，比如所有的所有的节点都只有右子树，变成个瘸腿将军，此时就会退化成单链表，查找复杂度达到O（n）

为了避免这种情况，我们还有平衡二叉树（AVL）和红黑树（RBT），不过今天先不讨论这两个，以后有空再补上

创建二叉查找树

首先我们需要定义一个Node类，存储自身的值和对两个儿子的指针
并且定义有一个插入节点的方法

class Node {
    constructor(data) {
    this.data = data
    this.left = null
    this.right = null
    }
    insertNode(newNode) {
        if (newNode.data < this.data) {
            if (this.left === null) { this.left = newNode }
            else {
                this.left.insertNode(newNode)
            }
        }
        else {
            if (this.right === null) { this.right = newNode }
            else {
                this.right.insertNode(newNode)
            }
        }
    }
}

然后定义一个BST类，接受一个数组进行初始化

class BinarySearchTree {
    constructor(arr) {
        this.root = new Node(arr[0])
        if (arr.length === 1) return;
        for (let i = 1; i < arr.length; i++) {
            this.root.insertNode(new Node(arr[i]))
        }
    }
}

通过传一个数组进去，就完成了我们的二叉查找树的初始化

var BST = new BinarySearchTree([9, 6, 11, 7, 19, 8, 20, 5])

打印出来大概长这样

插入

当想插入新的节点的时候，直接这么调用就可以了

this.root.insertNode(new Node(data))

广度遍历

广度遍历就是一层一层进行遍历，从上到下，从左至右
最后返回一个数组

breadthTraversal() {
    var queue = [this.root]
    var node
    var arr = []
    while (queue.length > 0) {
        node = queue.shift()
        arr.push(node.data)
        if (node.left) queue.push(node.left)
        if (node.right) queue.push(node.right)
    }
    return arr
}

深度遍历（递归）

深度遍历分为三种，前序遍历，中序遍历，后序遍历
这里需要强调的是，它们其实在遍历的走向上是一样的，只是什么时候才算真正遍历到了这个元素上有所分歧，可以看一下这篇文章的动画，瞬间理解
juejin.cn/post/684490…

首先我们很容易想到的是递归

//前序遍历
preOrder(arr = [], node = this.root) {
    if (node === null) return arr;
    arr.push(node.data)
    this.preOrder(arr, node.left)
    this.preOrder(arr, node.right)
    return arr;
}

那么中序遍历和后序遍历呢？
回想一下，他们三个唯一的区别只是在何时把节点的值加入数组
那么其实只要改一下arr.push(node.data)这句话的位置即可

//中序遍历
inOrder(arr = [], node = this.root) {
    if (node === null) return arr;
    this.inOrder(arr, node.left)
    arr.push(node.data)
    this.inOrder(arr, node.right)
    return arr;
}
//后序遍历
    postOrder(arr, node = this.root) {
    if (node === null) return arr;
    this.postOrder(arr, node.left)
    arr.push(node.data)
    this.postOrder(arr, node.right)
    return arr;
}

不过这也未免太简单了吧，我要是面试官我肯定不考这个
而且递归做法，在数据量很大的时候有爆栈的可能
所以下面我们要研究非递归的解法

深度遍历（非递归）

这里的关键是，我们要自己创建一个栈 var stack=[]
使用两个while循环，大循环保证遍历到所有节点，小循环是不断进行向左深入

//前序遍历
preOrder2() {
    var node = this.root
    var arr = []
    var stack = []
    while (node !== null || stack.length > 0) {
        while (node !== null) {
            stack.push(node)
            arr.push(node.data)
            node = node.left
        }
        //出来的时候node的左树已经遍历完了，此时是null
        if (stack.length > 0) {
            node = stack.pop()
            node = node.right
        }
        //出来后回到大循环的开始，又进入第一个小循环遍历左树
    }
    return arr
}

中序遍历的思想与其类似，我们也是只要改变arr.push(node.data)的位置即可

//中序遍历
inOrder2() {
    var node = this.root
    var stack = []
    while (node !== null || stack.length > 0) {
        while (node !== null) {
            stack.push(node)
            node = node.left
        }
        //出来的时候node的左树已经遍历完了，此时是null
        if (stack.length > 0) {
            node = stack.pop()
            arr.push(node.data)
            node = node.right
        }
        //出来后回到大循环的开始，又进入第一个小循环遍历左树
    }
    return arr
}

最难的是后序遍历，这里不是改变那句话的位置那么简单了
我们要改变一下思想了
想一想每个节点到底是什么时候算是被遍历到了的
就是在所有儿子都被遍历完了后，所以我们越先接触到的节点，就会越出现在最终的数组的末尾部分
所以我们只要把前序遍历的arr.push改成arr.unshift即可！

//后序遍历
postOrder2() {
    var node = this.root
    var stack = []
    while (node !== null || stack.length > 0) {
        while (node !== null) {
            stack.push(node)
            arr.unshift(node.data)  //最先接触到的节点最后才会被插入数组
            node = node.left
        }
        //出来的时候node的左树已经遍历完了，此时是null
        if (stack.length > 0) {
            node = stack.pop()
            node = node.right
        }
        //出来后回到大循环的开始，又进入第一个小循环遍历左树
    }
    return arr
}

查找最大最小节点

最小其实就是最左边那个节点，最大是最右边那个节点

searchMin(node = this.root) {
    if (node.left === null) return node;
    else {
        return this.searchMin(node.left)
    }
}
searchMax(node = this.root) {
    if (node.right === null) return node;
    else {
        return this.searchMax(node.right)
    }
}

查找指定节点

这个就是二叉查找树的强项了，基于二分思想的查找

hasNode(data, node = this.root) {
    if (node === null) return false;
    if (data === node.data) return true;
    else if (data < node.data) {
        return this.hasNode(data, node.left)
    }
    else {
        return this.hasNode(data, node.right)
    }
}

删除指定节点

这个分三种情况

叶子节点（没有儿子了）
节点只有左子树或右子树
节点既有左子树又有右子树

前两种好解决
第一种只要把叶子节点变成null即可
第二种就把它变成它的子树

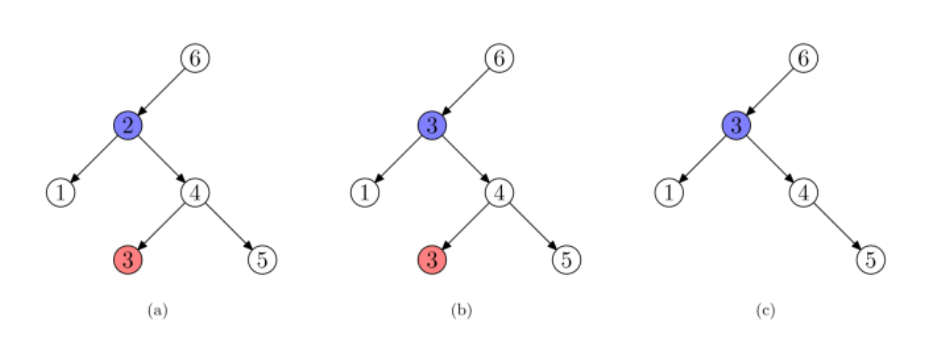
第三种稍微麻烦一点，要先找到待删除节点A的右子树中最小的那个节点B(也可以在左子树中找最大的），B就是整个右子树中最接近A的数值的了，然后令A.data=B.data，再把B节点删掉即可

delNode(data, node = this.root) {
    if (node === null) return 'not found';
    //找到了
    if (data === node.data) {
        //是叶子节点
        if (node.left === null && node.right === null) {
            node = null
        }
        //只有左子树或者右子树
        else if (node.left === null && node.right !== null) {
            node = node.right
        }
        else if (node.right === null && node.left !== null) {
            node = node.left
        }
        //左右子树都有
        else {
            var replaceNode = this.searchMin(node.right)
            node.data = replaceNode.data //掉包掉好了，接下去就是删除那个最小节点
            return this.delNode(node.data, node.right)
        }
    }
    //没找到，继续向下找
    else if (data < node.data) {
        return this.delNode(data, node.left)
    }
    else {
        return this.delNode(data, node.right)
    }
}

最大深度

返回当前二叉树的最大深度
使用分治思想，先向下不断分，再由底向上返回汇总

maxDepth(node = this.root) {
    if (node === null) return 0;
    return Math.max(this.maxDepth(node.left), this.maxDepth(node.right)) + 1
}

总结

学好二叉树不止是为了面试，从中也能更好得理解递归与分治的思想，并感受数据结构的魅力

这是我的个人网站，记录下前端学习的点滴，欢迎大家参观
www.ssevenk.com

你想要了解的二叉树（JS版）

树

二叉树