算法概述
在使用RecyclerView时,会经常遇到数据变化需要刷新列表的情况,如果数据变化非常频繁,而且每次都只改变了其中的一小部分,在这种情况下,通过Adapter.notifyDataSetChanged()直接对整个列表进行刷新会对app的性能带来影响。实际上,Adapter也提供了一系列的方法来刷新发生变化的数据,如notifyItemChanged、notifyItemMoved等,但是在使用这些方法时,就需要对数据的变化进行计算,而且为了达到最好的性能表现,这个计算也不能太过复杂,否则就违背了减少性能损耗的初衷,而DiffUtil,就是对这一计算过程的封装。
DiffUtil是support包V25版本引入的工具类,用于计算两个List之间的差异,并且得到一个可以将旧的List转换成新的List的编辑脚本,这个结果会被封装成DiffResult。在计算量很大的时候,可以使用AsyncListDiffer在后台进程中进行计算,然后在主线程中获取DiffResult并应用到RecyclerView中。
在DiifUtil中,计算List间的差异,并得到编辑过程的算法是Myers差分算法,这个算法将通过有向无环图来表示将旧的序列转换成新序列的过程,然后在这个图中能连通左上和右下顶点的最短的路径就是问题的最优解。算法的具体过程如下:
假设旧的序列A=a1,a2,a3……an,目标序列B=b1,b2,b3……bm 是两个长度分别为n和m的序列。以A序列为横轴坐标,B序列为纵轴坐标,通过边连接相邻的点,横边连接右邻点,竖边连接下邻点。如果存在点(x,y)使ax = by,则在(x-1,y-1)和(x,y)之间增加一条斜边,(x,y)称做匹配点。例如,对于序列A=ABCABBA以及序列B=CBABAC得到的编辑图如下:
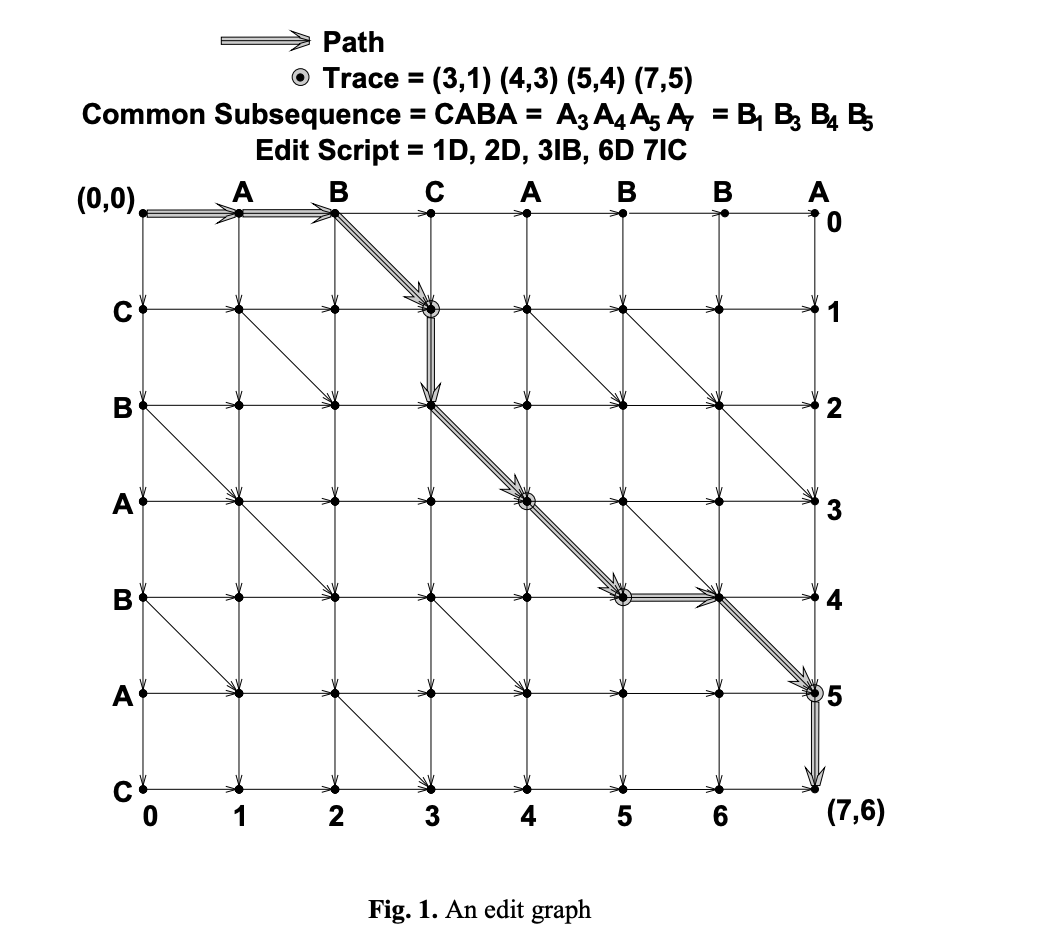
在DiffUtil中,通过查找位于目标D-path中间的斜线,将查找区域分隔成斜线的左上方和右下方两个子区域,然后对子区域进行递归查找的方式来得到。Myers在论文中证明了对于能达到最远点的(K,D-Path)对,可以通过(K-1,(D-1)-Path)通过贪心查找来得到。
算法实现
具体的实现如下:
while (!stack.isEmpty()) {//stack就是需要进行查找的区域
Range range = stack.remove(stack.size() - 1);
//得到D-Path中的斜线
Snake snake = diffPartial(callback, range.oldListStart, range.newListStart,
range.oldListEnd, range.newListEnd, forward, backward, max);
if (snake != null) {
if (snake.size > 0) {
//snake的长度大于0,是一个有效的子序列
snakes.add(snake);
}
//得到的子序列是以区域的左上角为原点的,需要经过二次处理还原为正确的结果
snake.x += range.oldListStart;
snake.y += range.newListStart;
//根据找到的斜线对剩下的区域进行划分
Range left = rangePool.isEmpty() ? new Range() : rangePool.remove(rangePool.size() - 1);
left.oldListStart = range.oldListStart;
left.newListStart = range.newListStart;
if (snake.reverse) {
left.oldListEnd = snake.x;
left.newListEnd = snake.y;
} else {
if (snake.removal) {
left.oldListEnd = snake.x - 1;
left.newListEnd = snake.y;
} else {
left.oldListEnd = snake.x;
left.newListEnd = snake.y - 1;
}
}
//加入栈中
stack.add(left);
//将右下区域压入栈的过程省略
....
}
//省略
....
}
从这个方法中可以发现,在DiffUtil中得到的斜线有两个布尔型属性reverse和removal,这两个属性是在diffPartical函数中查找斜线时赋值的,diffPartical函数的返回值是能以最短的步数连接区域左上顶点和右下顶点的斜线,reverse为true表示这个斜线是在反向查找时得到的,removal为true表示这个斜线的上一步是沿横线移动,即移除元素。那么这两个参数又是怎么得到的呢?在diffPartical函数中,通过同时从左上顶点和右下顶点出发,找到某个D值,使从左上顶点出发能到达的点位于从右下顶点出发能到达的点的右下方,则这两个到达点就位于目标斜线的两端。很显然,在实现中,从左上顶点出发和从右下顶点出发这两个过程是交替进行的,而不是并行的,那就需要在两个过程中都进行一次判断,reverse属性就表示了diffPartical得到的结果是在反向查找中得到的还是在正向查找中得到的。在diffPartical函数中还有额外的判断,在两个序列的长度差是偶数时,在正向查找时就能找到贯通线,否则就是在反向查找中才能找到。对于removal属性,先回顾一下k-线的概念,可以很简单的得到当k=d时,只能从(d-1)-path上的k-1线右移到达k-线,当k=-d时,只能从(d-1)-path上的-k+1线下移到达k-线,其他情况下,(d,k)可以由(d-1,k+1)或(d-1,k-1)到达,而从(d-1,k+1)到达(d,k),是沿竖线下移,新增元素,removal就是false,从(d-1,k-1)到达(d,k)就是沿横线右移,删除元素,removal为true。diffPartical的具体实现如下:
public static Snake partical(DiffCallback cb, int startOld, int startNew, int endOld, int endNew, int[] forward, int[] backward, int kOffset) {
//数组的下标不能取负,通过offset来处理k<0的情况
int oldSize = endOld - startOld;
int newSize = endNew - startNew;
if (endOld - startOld < 1 || endNew - startNew < 1) {
return null;
}
int dLimit = (oldSize + newSize + 1) / 2;//d的最大值不会超过长度的平均值
int delta = oldSize - newSize;
/**
* forward和backward记录每一步能到达的最远点的x坐标,forward记录从(0,0)正向查找,backward记录从(m,n)开始的反向查找
* 这一步预先填充起始点的位置
*/
Arrays.fill(forward, kOffset - dLimit - 1, kOffset + dLimit + 1, 0);
Arrays.fill(backward, kOffset - dLimit - 1 + delta, kOffset + dLimit + 1 + delta, oldSize);
/**
* 这个标志的含义就是认为在delta是偶数时,在正向查找时就能找到贯通线,否则找不到。如何证明?
* 先从delta = 0时考虑,两个序列长度相等,kBackward = k,正向查找和反向查找是一致的,由于先进行正向查找,所以必定会在正向查找时得出结果
* 假定能d=d0时在k0线找到的点为(x0,y0)开始的长度为l的线。
* 向newList插入一个点y1,此时delta = 1;三种情况
* 1.y1 > y0+l 即原先的贯通线仍然保留,则d=d0时,正向查找会到达k0线上的(x0+l,y0+l),反向查找在k0线上是(x0+1+l,y0+1+l),无法找到贯通线
* 而在d=d0+1时,正向查找会达到(x0+l+1,y0+l)(删除优先),此时还没进行新的反向查找,是与(x0+1+l,y0+1+l)对比不会得出结果,进行反向查找后,会
* 达到(x0,y0),得出结果
* 剩下的情况类似。
* 应该是这样证明,不保证正确性。
*/
boolean checkInFwd = delta % 2 != 0;
for (int d = 0; d < dLimit; d++) {
/**
* 这一循环是从(0,0)出发找到移动d步能达到的最远点
* 引理:d和k同奇同偶,所以每次k都递增2
*/
for (int k = -d; k <= d; k += 2) {
int x;
boolean removal;
/**
* K-线可以由(K+1)-线或(K—1)-线到达,判断哪一个能达到更远的位置,k=-d时,只能是从k+1线向下移动到达,此时的x为起始位置的x
* forward[kOffset + k - 1] < forward[kOffset + k + 1]表明k+1的位置更远
*/
if (k == -d || (k != -d && forward[kOffset + k - 1] < forward[kOffset + k + 1])) {
//从K+1线到K线的过程是x不变,y=y+1,即增加新元素
x = forward[kOffset + k + 1];
removal = false;
} else {
//从K-1线到K线的过程是y不变,x=x+1,即移除旧元素
x = forward[kOffset + k - 1] + 1;
removal = true;
}
//k = x-y,知道k和x,就可以得到y
int y = x - k;
//沿斜线移动到最远的位置
while (x < oldSize && y < newSize
&& cb.areContentSame(startOld + x, startNew + y)) {
x++;
y++;
}
//移动过后的x就是当前的d下,从(0,0)出发,在k线上最远的位置,经过对k的循环后,就是当前d下能达到的最远点
forward[kOffset + k] = x;
if (checkInFwd && k >= delta - d + 1 && k <= delta + d - 1) {//TODO 这一步没看懂,为什么是在k<=delta-d+1
/**
* 如果在k线上正向查找能到到的位置的x坐标比反向查找达到的y坐标小
* Xf > Xb
* Kf = kB
* 则Yf > Yb
* 即反向查找达到的最远位置在正向查找达到的位置的左上角,由于都在同一k线上,所以这两个点必定位于一条斜线的两端
*/
if (forward[k + kOffset] >= backward[k + kOffset]) {
Snake outSnake = new Snake();
outSnake.x = backward[k + kOffset];
outSnake.y = outSnake.x - k;
outSnake.size = forward[k + kOffset] - backward[kOffset + k];//两个点位于一条斜线的两端,那么斜线的长度也就是x的差值
outSnake.removal = removal;
outSnake.reverse = false;
//到这一步就是找到了起始点为(x,x-k),长为size的斜线,也就是公共子序列
return outSnake;
}
}
}
/**
* 这一循环是从(m,n)出发找到移动d步能达到的最远点
*/
for (int k = -d; k <= d; k += 2) {
/**
* 同样的,k线可以从k-1线和k+1线到达,与正向查找的情况不太一样的是,反向查找是从delta线出发的,所以需要经过一次转换
* kBackward = k + delta;
* 简单的称之为k差线
*/
int kBackward = k + delta;
int x;
boolean removal;
/**
* 与k线类似,k差线可以由k-1差线和k+1差线到达,但是这里的最远的点是x最小的位置。
* kBackward = d + delta 时,只能从kBackward -1 向上移动得到,x不变
* kBackward = -d + delta,只能从kBackward + 1向左移动得到
* 由于是反向的查找,只能向上或向左移动,因此这一步对kBackward = d+delta时,即k=d时进行特殊处理
*/
if (kBackward == d + delta || (backward[kBackward + kOffset - 1] < backward[kBackward + kOffset + 1])) {
x = backward[kOffset + kBackward - 1];
removal = false;
} else {
x = backward[kOffset + kBackward + 1] - 1;
removal = true;
}
/**
* 因为在k差线上,所以y=x-kBackward
*/
int y = x - kBackward;
while (x > 0 && y > 0
&& cb.areContentSame(startOld + x - 1, startNew + y - 1)) {
x--;
y--;
}
//在k差线上的点也在k+delta线上,直接存就完事了
backward[kOffset + kBackward] = x;
if (checkInFwd && k + delta >= -d && k + delta <= d) {//TODO 同样没看懂
/**
* 在kBackward线上的看正向反向是否连通了
*/
if (forward[kOffset + kBackward] >= backward[kOffset + kBackward]) {
Snake outSnake = new Snake();
outSnake.x = backward[kOffset + kBackward];
outSnake.y = outSnake.x - kBackward;
outSnake.size = forward[kOffset + kBackward] - backward[kOffset + kBackward];
outSnake.removal = removal;
outSnake.reverse = true;
return outSnake;
}
}
}
}
//没找到就抛异常,正常情况下不可能找不到,对d的遍历最大可以到2*Math.max(oldListSize,newListSize),沿着坐标轴走也走到了
throw new IllegalStateException("DiffUtil hit an unexpected case while trying to calculate"
+ " the optimal path. Please make sure your data is not changing during the"
+ " diff calculation.");
}
到这一步,就得到了一个目标D-path上的所有的斜线的集合,将斜线连接,得到最终的路径的过程在DiffResult中。
DiffResult
在介绍DiffResult之前,首先需要了解,在Myers算法中,当多个元素在List中移动时,Myers算法可能会选择其中的一个作为锚点,将这个点标记为无变化的同时将其他的点标记为增加或移除。而被标记为NOT_CHANGED的点只是不会被分发为 移动/增加/删除,而不是真的仍然在序列中保持原样。
在DiffResult的构造方法中,首先会检查一下calculateDiff得到的斜边集合的起点,也就是第一条snake,如果这条线不是从(0,0)开始的,那就增加一条长度为0,位于(0,0)的线作为起始点。这样在对Snakes从头到尾遍历一次时,就可以完成从(0,0)到(m,n)的通路。
Snake firstSnake = mSnakes.isEmpty() ? null : mSnakes.get(0);
if (firstSnake == null || firstSnake.x != 0 || firstSnake.y != 0) {
Snake root = new Snake();
root.x = 0;
root.y = 0;
root.removal = false;
root.size = 0;
root.reverse = false;
mSnakes.add(0, root);
}
在增加起始点之后,DiffResult的构建方法中还会进行一个状态的初始化,在这个过程中,会从后到前的遍历每一个Snake。
//从最后一个item开始,遍历全部的Snake中的全部节点
for (int i = mSnakes.size() - 1; i >= 0; i--) {
final Snake snake = mSnakes.get(i);
final int endX = snake.x + snake.size;
final int endY = snake.y + snake.size;
if (mDetectMoves) {
.....//先忽略这一步
}
for (int j = 0; j < snake.size; j++) {
final int oldItemPos = snake.x + j;
final int newItemPos = snake.y + j;
final boolean theSame = mCallback
.areContentsTheSame(oldItemPos, newItemPos);
//这个标记item是否发生改变,在DiffResult中,这种标志有五位,FLAG_OFFSET=5,此外还有一个值为0b11111的掩码FLAG_MASK
final int changeFlag = theSame ? FLAG_NOT_CHANGED : FLAG_CHANGED;
//将状态放入表中,newItemPos这个数的影响实际上会在之后与掩码的与计算中被消除,实际起作用的是changeFlag
mOldItemStatuses[oldItemPos] = (newItemPos << FLAG_OFFSET) | changeFlag;
mNewItemStatuses[newItemPos] = (oldItemPos << FLAG_OFFSET) | changeFlag;
}
posOld = snake.x;
posNew = snake.y;
}
在不考虑detectmove的情况下,DiffResult的构建已经完成,在这之后可以就可以调用dispatchUpdateTo(ListUpdateCallback updateCallback)方法将变化分发到执行变化的回调中,这一步的参数可以直接传入Adapter,也可以传入自己实现的UpdateCallback。区别在于直接传入Adapter的话会创建一个新的AdapterListUpdateCallback对象。分发时,也会从最后一个snake开始对snakes进行一次遍历
for (int snakeIndex = mSnakes.size() - 1; snakeIndex >= 0; snakeIndex--) {
final Snake snake = mSnakes.get(snakeIndex);
final int snakeSize = snake.size;
final int endX = snake.x + snakeSize;
final int endY = snake.y + snakeSize;
//如果snake的最右、最下的点位于上一个snake点的左边则说明从上一个snake到这一个之间存在移除的过程。不清楚的话可以在回顾一下编辑图
if (endX < posOld) {
dispatchRemovals(postponedUpdates, batchingCallback, endX, posOld - endX, endX);
}
//如果snake的最右、最下的点位于上一个snake点的上边则说明从上一个snake到这一个之间存在增加的过程。
if (endY < posNew) {
dispatchAdditions(postponedUpdates, batchingCallback, endX, posNew - endY,
endY);
}
//对于斜线上的点还需要判断一次是否发生改变
for (int i = snakeSize - 1; i >= 0; i--) {
if ((mOldItemStatuses[snake.x + i] & FLAG_MASK) == FLAG_CHANGED) {
batchingCallback.onChanged(snake.x + i, 1,
mCallback.getChangePayload(snake.x + i, snake.y + i));
}
}
posOld = snake.x;
posNew = snake.y;
}
dispatchRemovals和dispatchAdditions方法内部非常简单,就是对这些点进行遍历,然后从状态表中查询它们的状态,并根据状态进行分发。到这一步,detected参数为false时,差异计算、结果分发过程就完成了,adapter或者UpdateCallback会根据接收到的结果进行对应的刷新。detected为true时,会在构造DiffResult初始化状态时增加一个步骤,在遍历snake时,如果存在被移除的节点,会从剩余的未遍历的snake中进行一次查找,看看是否有相同的item被增加,如果是增加的节点则是查找是否存在内容相同的移除过程。
private void findMatchingItems() {
...//省略
for (int i = mSnakes.size() - 1; i >= 0; i--) {
...//省略
if (mDetectMoves) {
while (posOld > endX) {
// this is a removal. Check remaining snakes to see if this was added before
findAddition(posOld, posNew, i);
posOld--;
}
while (posNew > endY) {
// this is an addition. Check remaining snakes to see if this was removed
// before
findRemoval(posOld, posNew, i);
posNew--;
}
}
...//省略
}
}
以上就是DiffUtil的全部内容,总结一下:
- 通过编辑图的方式表示两个序列的转换过程,向右移动表示删除,向下移动表示增加,将问题转换为寻找编辑图中的最短路径问题。
- 通过查找递归查找贯通线的方法得到寻找最短路劲的解
- 遍历最短路径标记每个节点的状态,然后根据状态进行分发