定义
栈是一种特殊的线性表,它只能在一端进行插入或者删除操作,能进行操作的一端称为栈顶,另一端则称为栈底。也由于这个特性,导致先进入的元素,只能后出,因此栈是后进先出的线性表。
栈是一种线性表,因此它的存储可以是链式存储,也可以是顺序存储。链式存储的栈,称为链栈,顺序存储的栈,称为顺序栈。而下面实例中,使用go语言的可变数组slice完成栈的存储,因此是顺序存储。
栈的描述
type data interface {}
type Stack struct {
top int // 栈顶,代表栈顶的下标,-1为空栈
list []data // 从0开始存储
}
func New() *Stack{
s := &Stack{top:-1,list: []data{}}
return s
}
主要操作
入栈
在栈顶插入一个新元素,称为入栈,首先要判断栈是否已满,满就报错,否则就插入,并将栈顶上升一位。
// 由于使用的是可变数组,因此不会出现栈满的情况,所以以下代码不需要判断是否栈满,如果是不可变数组,或者是限制容量的栈,则要判断栈是否已满
func (s *Stack) Push (value data) {
s.list = append(s.list,value)
s.top++
}
出栈
取出栈顶元素,并将栈顶下降一位,如果栈为空,则报错
func (s *Stack) Pop() (data,error) {
if s.top == -1 {
return nil,errors.New("栈空")
}
data := s.list[s.top]
s.list = s.list[:s.top]
s.top--
return data,nil
}
判空
判断是否为空栈
func (s *Stack) IsEmpty() bool{
return s.top == -1
}
获取栈顶元素
得到栈顶元素的值,但不出栈
func (s *Stack) GetTop() data{
if s.top == -1 {
return nil
}
return s.list[s.top]
}
}
应用:算术表达式求值
后缀表达式
我们日常生活中使用的算术表达式,例如:5+6/2-3*4,它由两类对象构成:
- 运算数,如:5,6,2等
- 运算符号,如+,-等,而且不同运算符号优先级不一样
由于运算符号优先级不同,而且运算符号位于运算数中,所以使得运算变得复杂了。 怎么理解呢?拿上面的表达式为例,当程序遍历到+号的时候,要做+运算,那么是5+6吗?很显然不是,因为6后面还有一个/运算符,而且/的优先级大于+,所以6是/的运算数,而不是+的运算数。那么反过来呢?当遍历到一个运算符号的时候,就已经知道对应的两个运算数,这样求值就变的简单了。伟大的科学家们,就此发明了后缀表达式,也称逆波兰式,指的是不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则)。
- 中缀表达式:2 + 9 / 3 - 5
- 后缀表达式:2 9 3 / + 5 -
当然两个表达式,都是表达同一个意思。
后缀表达式求值
由于后缀表达式不需要考虑运算符的优先规则,因此求值算法就变得简单了:
1、从左到右依次遍历表达式;
2、遇到数字就直接入栈;
3、遇到操作符就弹出两个元素,先弹出的元素放到操作符的右边,后弹出的元素放到操作符的左边(左边的运算数先入栈,因此后出),将计算得到的结果再压入栈;
4、直到整个表达式遍历完,最后弹出的栈顶元素就是表达式最终的值。
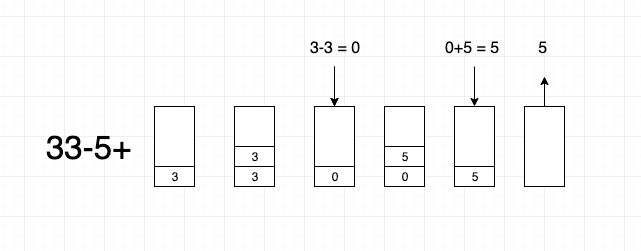
以33-5+表达式为例,运行状态如下
func getPostfixExpressionResult(s string) int {
stack := Stack.New()
for _, value := range s {
if unicode.IsDigit(value) {
intValue, _ := strconv.Atoi(string(value))
stack.Push(intValue)
} else {
right, _ := stack.Pop()
left, _ := stack.Pop()
result := calculate(left.(int), right.(int), string(value)) // 封装的 + - * / 求值方法
stack.Push(result)
}
}
result, _ := stack.Pop()
return result.(int)
}
getPostfixExpressionResult("33-5+") // 5
可以看得出算法时间复杂度为O(n),并且通过出栈入栈的形式就可以完成求值过程。
中缀表达式转后缀表达式
接下来看看中缀怎么转后缀,我们先对比一下两个表达式:
- 中缀表达式:2 + 9 / 3 - 5
- 后缀表达式:2 9 3 / + 5 -
可以看的出来,数字的相对位置是不变的,改变的是符号的位置,那么在转换的过程,我们需要对比各种运算符号的优先级,然后将优先级高的运算符,先输出,低的后输出,这样在后缀表达式求值的时候,就能保存计算顺序不被改变。(左括号和右括号也看成运算符号)具体的算法步骤如下:
1、从左到右遍历中缀表达式;
2、如果是运算数,直接输出;
3、如果是运算符号:若优先级大于栈顶的运算符号(栈不为空),则将该运算符号压入栈中,因为如果该运算符号优先级比栈顶的大,说明要先被计算,那么它是后入的,因此在之后的操作中,一定比栈顶的符号先出,因此在后缀求值中,肯定先被计算;
4、如果是运算符号:若优先级小于等于栈顶的运算符号(栈不为空),则将栈顶的运算符号弹出并输出,然后继续和下一个新的栈顶元素对比,直到优先级大于新的栈顶元素,就将该运算符号压入栈中;
5、左括号:括号里的表达式肯定是要先计算的,因此当扫描到左括号的时候,直接将左括号压入栈中,而入了栈里的左括号,优先级就变到最低了。因为括号里的运算符要先运算;
6、右括号:将栈顶元素弹出并输入,直到遇到左括号(弹出,但不输出);
7、整个表达式遍历完之后,则将栈里的元素一一弹出并输出。
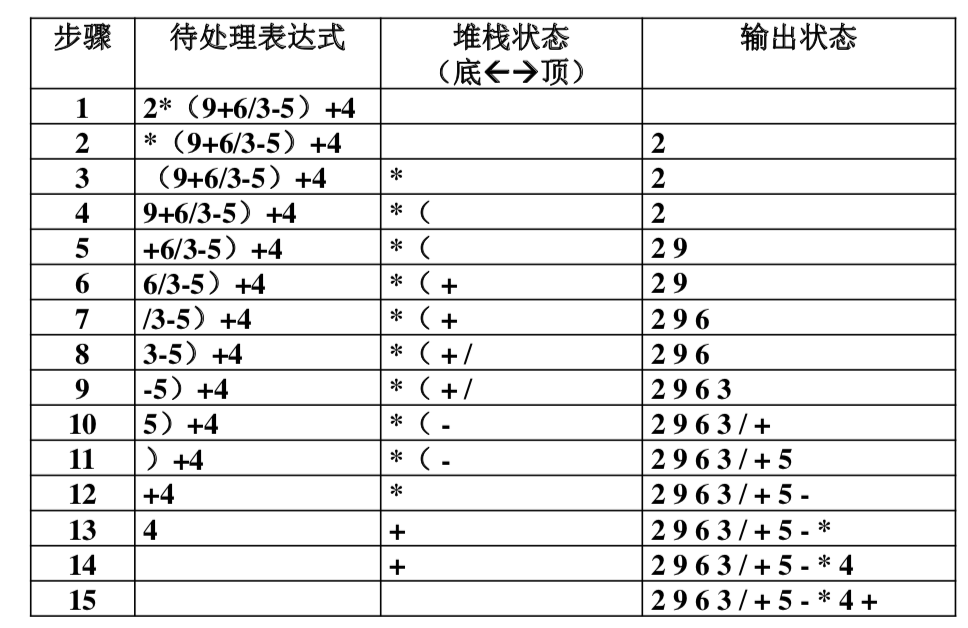
我们以2*(9+6/3-2)+4为例:
// 利用hash的形式来判断运算符号的优先级
// 有兴趣可以看看百度百科里(后缀表达式)是怎么判断运算符号优先级的,很有意思 (>▽<)
var opPriority = map[string]int{
"*":2,
"/":2,
"+":1,
"-":1,
"(":0,
}
func infixToPostfix(s string) string{
postfix := ""
stack := Stack.New()
for _,value :=range s{
if unicode.IsDigit(value) {
postfix += string(value)
} else {
op := string(value)
switch op{
case "+","-","*","/":
if stack.IsEmpty(){
stack.Push(op)
} else {
pop := stack.GetTop()
for opPriority[op] <= opPriority[pop.(string)] {
pop,_ = stack.Pop()
postfix += pop.(string)
if stack.IsEmpty() {
break
}
pop = stack.GetTop()
}
stack.Push(op)
}
case "(":
stack.Push(op)
case ")":
for !stack.IsEmpty() {
op,_ := stack.Pop()
if op.(string) == "(" {
break
}
postfix +=op.(string)
}
}
}
}
for !stack.IsEmpty(){
op,_ := stack.Pop()
postfix +=op.(string)
}
return postfix
}
infixToPostfix("2*(9+6/3-5)+4") // 2963/+5-*4+
总结
栈是一种被广泛应用的数据结构,除了刚刚举例的算术表达式求值之外,栈还用于函数调用及递归实现,回溯算法等等。在适当的时候选择栈,可以更加高效的解决问题。
ps:在上面的例子里,后缀表达式求值的程序,是一个不太正确的程序,准确的讲,它会把每个数字看成运算数,即122*,它不会计算出24,而是变成了4,估计大家也猜到原因了,因为程序是一个字符一个字符的遍历,而没有位数的划分,修正的话,可以用数组来存表达式,这样就可以正确的划分运算数。
Thanks!