概率于Machine Learning而言还是比较重要的,但是概率的难点在于,其不够直观,那么换一个视角,我们称之为"上帝视角",将概率转化为面积,这样便会变的直观;
1.概率的定义
概率,顾名思义就是某事件发生可能性的一种量化,这是我们最直观的感受;
下面从一个比较经典的案例来作为引入 — 蒙提霍尔问题:
有ABC三扇门,其中有一扇是正确的门,打开有一辆豪车,其余两扇,门为错误的门,门内有山羊: 前提:骰子1,2对应门1;骰子3,4对应门2,骰子5,6对应门3
-
- 主持人通过投骰子,决定将豪华车放入哪个门内
-
- 选手通过掷骰子决定打开那一扇门
-
- 选手选择完毕之后,主持人会打开剩余两扇门中错误的一扇门,然后询问选手是否改变主意
下面来看概率:
- 如果第一次选择正确,重选必定错误
- 如果第一次选择错误,重选必定正确
所以"第一次选择错误"的概率就是"重选后正确"的概率,其重选的正确率就是 2/3
但是其实也会有另一种误区:
第一选择完毕后,主持人打开一个错误的门,那么此时就剩下一个错误的门和一个正确的门,此时重选的概率就是: 假如主持人打开的错误门是门1;
- 门2是正确答案的概率: 1/2
- 门3是正确答案的概率: 1/2
但是仔细一想,这种概率是建立在,选手没有进行第一次选择的基础上进行的;
2.飞艇角度来看蒙提霍尔问题
正如上面的误区,概率是一个抽象的东西,有时候我们会掉进这个误区中出来
概率是一种抽象的概念,如果我们仅仅凭直觉判断,很难清晰理解它的本质
我们的思路是这样:
1.转换视角来看待这个问题(这里是飞艇视角)
2.尽量把问题转换成一种可以实际衡量的形式
场景是这样的:
- 将剧本设定为360个会场中有120个会场的门1是正确答案,120个会场的门2是正确答案,120个会场是门3是正确答案
- 然后门1是正确答案120个会场中,有40个挑战者选择门1,有40个挑战者选择门2,有40个挑战者选择门3

根据上表,我们来复原刚刚的误区:
- 1.挑战者选择门3
- 2.主持人打开门1的有60个会场
- 3.其中门2是正确答案是40个,门3是正确答案是20个,所以证明刚刚是错误的
3.上帝视角来看概率
-
这时候我们需要来看一个概念三元组:
( Ω,F ,P ) (Ω,F,P) (\Omega,F,P) (Ω , F, P )
何为上地视角,其实就是一种鸟瞰的视角,每一个会场(其实就是一个世界,也可以认为一种可能出现的场景就是一个世界),对于特定的世界来说,当前世界的剧本已经被锁定;
举一个简单的例子:
随机投一枚骰子,共有6种结果:结果为1是一个世界,结果为2也是一个世界,同理3,4,5,6 亦是如此…,而我们从"上地视角",俯瞰这些世界; -
场景:投硬币
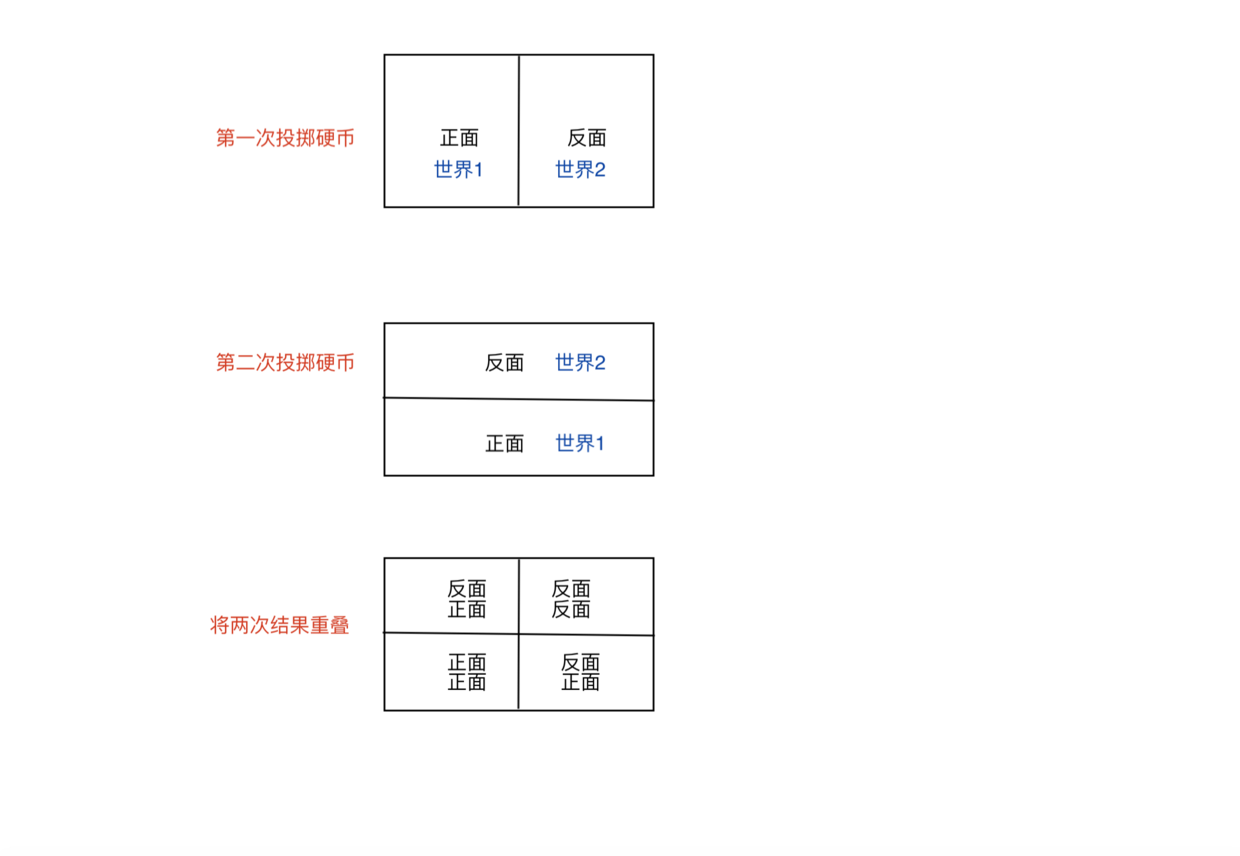
- 每个世界的抛硬币的结果是永远不变的
- 然后人们不知道身处哪一个世界,所以不确定性就会产生
到目前为止,我们便已经将一个抽象的概念:概率,转化为一个可量化的概念(面积量化)
这里我们来用几个数学符号:
Ω :代 表所 有平 行世 界的 合集 ,也 就是 所有 可能 场景 的集 合; ω是 每 一 个 世 界 的 映 射 . eg :ω 1,ω 2... Ω:代表所有平行世界的合集,也就是所有可能场景的集合;ω是每一个世界的映射.eg:ω1,ω2... \Omega:代表所有平行世界的合集,也就是所有可能场景的集合; \omega是每一个世界的映射.eg: \omega1, \omega2... Ω: 代表 所有平行 世界的合 集 ,也 就是 所有 可能场景 的集合; ω是 每一个 世 界的映射 .eg : ω1, ω 2...
P 是 每 一 个 世 界 的 面 积 ,这 里 我 们 需 要 知 道 所 有 的 平 行 世 界 的 面 积 为 1 , 或 者 可 以 这 样 理 解 , Ω 是 所 有 平 行 世 界 的 合 集 , P是每一个世界的面积,这里我们需要知道所有的平行世界的面积为1,或者可以这样理解,Ω是所有平行世界的合集, P是每一个世界的面积,这里我们需要知道所有的平行世界的面积为1,或者可以这样理解,\Omega是所有平行世界的合集, P是每 一 个世 界的面 积, 这 里我 们需 要 知 道所 有的 平行 世界 的面 积为 1, 或 者 可 以 这 样 理 解 , Ω 是 所 有 平 行 世 界 的 合 集 ,
当 然 从 数 学 角 度 来 看 他 只 是 一 个 面 , Ω 是 点 的 集 合 , 对 于 Ω 中 人 意 一 点 A , 其 发 生 的 概 率 ,
当
然
从
数
学
角
度
来
看
他
只
是
一
个
面
,
Ω
是
点
的
集
合
,
对
于
Ω
中
人
意
一
点
A
,
其
发
生
的
概
率
,
当然从数学角度来看他只是一个面,\Omega是点的集合,对于\Omega中人意一点A,其发生的概率,
当 然 从 数 学 角 度 来 看 他 只 是 一 个 面 , Ω 是 点 的 集 合 , 对 于 Ω 中 人 意 一 点 A , 其 发 生 的 概 率 ,
就 是 其 所 在 区 域 的 面 积 , 用 P ( A ) 表 示
就
是
其
所
在
区
域
的
面
积
,
用
P
(
A
)
表
示
就是其所在区域的面积,用P(A)表示
就 是 其 所 在 区 域 的 面 积 , 用 P ( A ) 表 示
这样的话就知道三元组的第一个和第三个参数意义,第二个参数这里暂且跳过
这样概率便转化为面积,任何量化的东西,要比抽象的概念理解起来更加舒服,深刻;
这 里补 充一 下, 每个 世 界 ω 可 以 理 解 为 样 本 , 由 所 有 平 行 世 界 组 成 的 Ω就 是 样 本 空 间 ,Ω 的 子 集 A就 是 事 件 ,我 们 日 常 的 讨 论 的 概 率 应 当 是 基 于 事 件 取 量 化 的 这里补充一下,每个世界ω可以理解为样本,由所有平行世界组成的Ω就是样本空间,Ω的子集A就是事件,我们日常的讨论的概率应当是基于事件取量化的 这里补充一下,每个世界\omega可以理解为样本,由所有平行世界组成的\Omega就是样本空间,\Omega的子集A就是事件,我们日常的讨论的概率应当是基于事件取量化的 这 里 补充一下 , 每个世 界ω可 以 理解为样本 ,由所 有平 行世界 组成的 Ω就 是样本空 间 ,Ω的 子 集A就是 事件 , 我们日 常 的讨论的 概 率应当 是基 于事 件取量 化 的
4.随机变量 & 概率分布
4.1 随机变量
注意这里的子集A仅仅是平面上的一个点,我们称为样本点或者基本事件会更加合适一些,打个比方,投掷硬币为正面向上的区域有无数个点,而当前的事件应该是正面朝上的事件,而点A仅仅是构成事件的样本点而已;
所 以进 一步 来看 ,随 机事 件是 会随 机改 变的 不确 定点 ,他 也是 由某 个世 界中 的点 集表 示 ,所 以 随 机 事 件 应 该 是 关 于 ω的 函 数 ,即 为 : 所以进一步来看,随机事件是会随机改变的不确定点,他也是由某个世界中的点集表示,所以随机事件应该是关于ω的函数,即为: 所以进一步来看,随机事件是会随机改变的不确定点,他也是由某个世界中的点集表示,所以随机事件应该是关于\omega的函数,即为: 所以 进 一步来 看, 随机事 件是 会 随机 改变 的 不 确定 点, 他 也是 由某 个 世 界中 的 点 集 表 示 , 所 以 随 机 事 件 应 该 是 关 于 ω 的 函 数 , 即 为 :
f (ω) f(ω) f(\omega) f( ω)
4.2 概率分布
随机变量是基于具体的平行世界的,相对的概率分布只考虑面积,比如投掷硬币:
- 正面:0.5
- 反面:0.5
5.事件的独立性
其实可以这样表述这个定义:事件A和时间B,如果P(A|B) = P(A|非B),那么我们就认为事件A和事件B相互独立
下面来介绍几个等价表诉:
- A与B相互独立
- P(A|B) = P(A|非B)
- P(A|B) = P(A)
- P(A,B) = P(A)P(B)
- P(A,B) : P(A,非B) = P(非A,B) : P(非A,非B)
所以判断事件A B 是否独立可以利用上诉的任意等价表诉来进行判断