目录
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 遍历方式的选择条件
- 根据遍历结果重构二叉树
- 翻转二叉树
- 计算二叉树的高度
- 判断一棵树是否为完全二叉树
一 前序遍历(Preorder Traversal)
访问顺序:`根节点,前序遍历左子树,前序遍历右``子树
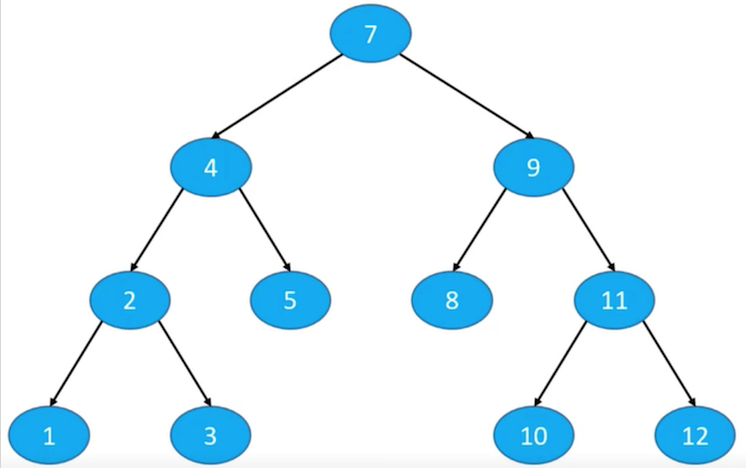
image.png
遍历顺序: [7],[4,2,1,3,5],[9,8,11,10,12]
带[]表示分割为根节点,左子树节点,右子树节点,下面类似
- 代码实现 - 递归
/// 前序遍历
- (void)preorder:(TreeNode *)node {
if (node == nil) {
return;
}
NSLog(@"%@",node.description);
[self preorder:node.left];
[self preorder:node.right];
}- 测试代码
/// 前序遍历
- (void)preorder {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
[tree preordr];
}运行结果

前序遍历.png
二 中序遍历(Inorder Traversal)
访问顺序:中序遍历左子树,根节点,中序遍历右子树
上图中序遍历结果:[1,2,3,4,5],[7],[8,9,10,11,12]
2.1 扩展
如果将访问顺序调整为:中序遍历右子树,根节点,中序遍历左子树
遍历结果:[12,11,10,9,8],[7],[5,4,3,2,1]
总结:二叉搜索树的中序遍历结果是升序或者降序的
- 代码实现 - 递归
/// 中序遍历
- (void)inorder:(TreeNode *)node {
if (node == nil) {
return;
}
[self inorder:node.left];
NSLog(@"%@",node.description);
[self inorder:node.right];
}- 测试代码
/// 中序遍历
- (void)Inorder {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
[tree inorder];
}运行结果
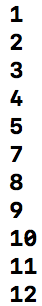
中序遍历.png
三 后序遍历(Postorder Traversal)
访问顺序:后序遍历左子树,后序遍历右子树,根节点
上图后序遍历结果:
[1,3,2,5,4],[8,10,12,11,9],[7]
代码实现 - 递归
/// 后序遍历
- (void)postorder:(TreeNode *)node {
if (node == nil) {
return;
}
[self postorder:node.left];
[self postorder:node.right];
NSLog(@"%@",node.description);
}- 测试代码
/// 后序遍历
- (void)postorder {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
[tree postorder];
}运行结果:
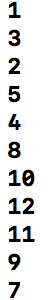
后序遍历.png
四 层序遍历(Level Order Traversal)
访问顺序:从上到下,从左到右,依次访问每一个节点
上图遍历结果:[7],[4,9],[2,5,8,11],[1,3,10,12]
实现思路:使用队列
1. 将根节点入队
2. 循环执行以下操作,直到队列为空
2.1 将队头节点A出队,进行访问
2.2 将A的左子节点入队
2.3 将A的右子节点入队- 代码实现 - 迭代
/// 层序遍历
- (void)levelOrder {
if (_root == nil) {
return;
}
Queue *queue = [[Queue alloc] init];
[queue enQueue:_root];
while (!queue.isEmpty) {
TreeNode *node = [queue deQueue];
NSLog(@"%@",node.description);
if (node.left != nil) { // 左子节点入队
[queue enQueue:node.left];
}
if (node.right != nil) { // 右子节点入队
[queue enQueue:node.right];
}
}
}- 测试代码
/// 层序遍历
- (void)levelOrder {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
[tree levelOrder];
}运行结果:
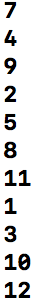
层序遍历.png
五 遍历的作用
- 前序遍历:树状结构展示(注意左右子树的顺序)
- 中序遍历:二叉搜索树的中序遍历按升序或者降序处理节点
- 后序遍历:适用于一些先子后父的操作
- 层序遍历:计算二叉树的高度,判断一棵树是否为完全二叉树
六 根据遍历结果重构二叉树
6.1 以下结果可以保证重构出唯一的一棵二叉树
- 前序遍历 + 中序遍历
- 后序遍历 + 中序遍历
image.png
6.2 前序遍历 + 后序遍历
- 如果它是一棵真二叉树,结果是唯一的
- 不然结果不唯一
七 前序遍历 + 中序遍历重构二叉树
八 利用前序遍历树状打印二叉树
- 代码实现如下
- (NSString *)description {
NSMutableString *strM = [NSMutableString stringWithString:@"\n"];
NSMutableString *prefix = [NSMutableString string];
[self toString:_root strM:strM prefix:prefix];
return strM.copy;
}
- (void)toString:(TreeNode *)node strM:(NSMutableString *)strM prefix:(NSMutableString *)prefix {
if (node == nil) {
return;
}
// 前序遍历二叉树
[self toString:node.left strM:strM prefix:[NSMutableString stringWithFormat:@"%@%@",prefix,@"L_"]];
[strM appendString:[NSString stringWithFormat:@"%@%@ \n",prefix,node.element]];
[self toString:node.right strM:strM prefix:[NSMutableString stringWithFormat:@"%@%@",prefix,@"R_"]];
}- 测试代码
/// 利用前序遍历树状打印二叉树
- (void)printBinarySearchTree {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
NSLog(@"%@",tree.description);
}运行结果

image.png
九 翻转二叉树
226. 翻转二叉树
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9输出:
4
/ \
7 2
/ \ / \
9 6 3 1- 代码实现如下
十 计算二叉树的高度
- 递归实现
/// 计算二叉树的高度 - 递归实现
- (int)getHeight {
return [self height:_root];
}
- (int)height:(TreeNode *)node {
if (node == nil) {
return 0;
}
return 1 + MAX([self height:node.left], [self height:node.right]);
}- 迭代实现
/// 计算二叉树的高度 - 迭代实现 - 层序遍历
- (int)getHeight2 {
if (_root == nil) {
return 0;
}
int height = 0; // 树的高度
int levelSize = 1; // 存储着每一层的元素数量
Queue *qu = [[Queue alloc] init];
[qu enQueue:_root];
// 遍历队列
while (!qu.isEmpty) {
TreeNode *node = qu.deQueue;
levelSize--;
if (node.left != nil) {
[qu enQueue:node.left];
}
if (node.right != nil) {
[qu enQueue:node.right];
}
if (levelSize == 0) { // // 意味着即将要访问下一层
levelSize = qu.size;
height++;
}
}
return height;
}- 测试代码
/// 计算二叉树的高度
- (void)getTreeHeight {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
NSLog(@"递归:%d",[tree getHeight]);
NSLog(@"递归:%d",[tree getHeight2]);
}- 运行结果

二叉树高度.png
十一 判断一棵树是否为完全二叉树
实现原理
1. 如果树为空,返回 false
2. 如果树不为空,开始层序遍历二叉树(使用队列)
2.1 如果node.left != nil && node.right != nil,将node.left,node.right按顺序入队列
2.2 如果node.left == nil && node.right != nil,返回false
2.3 如果node.left != nil && node.right == nil 或者 node.left == nil && node.right == nil,那么
2.3.1 后面遍历的节点都应该为叶子节点,才是完全二叉树
2.3.2 否则返回 false
2.4 遍历结果,返回 true- 代码实现如下
/// 是否为完全二叉树
- (BOOL)isComplteBinaryTree {
if (_root == nil) {
return false;
}
Queue *qu = [[Queue alloc] init];
[qu enQueue:_root];
BOOL leaf = false; // 是否为叶子节点
while (!qu.isEmpty) {
TreeNode *node = qu.deQueue;
if (leaf && !node.isLeaf) { // 处于最后一层了,要求是叶子节点才可以
return false;
}
if (node.hasTwoChildren) { // 有左右子树 - 都入队
[qu enQueue:node.left];
[qu enQueue:node.right];
} else if (node.left == nil && node.right != nil) { // 如果只有一个叶子节点,必须在左边才行
return false;
} else { // 后面遍历的节点都必须是叶子节点
leaf = true;
}
}
return true;
}- 测试代码
/// 是否为完全二叉树
- (void)isComplteBinaryTree {
NSArray *data = @[@7,@4,@9,@2,@5,@8,@11,@1,@3,@10,@12];
NSArray *data1 = @[@7,@4,@9,@2,@5,@8,@11];
NSArray *data2 = @[@7,@4,@9,@2,@5,@8,@11,@1];
BinarySearchTree *tree = [[BinarySearchTree alloc] init];
for (int i = 0; i < data.count; i++) {
[tree add:data[i]];
}
BinarySearchTree *tree1 = [[BinarySearchTree alloc] init];
for (int i = 0; i < data1.count; i++) {
[tree1 add:data1[i]];
}
BinarySearchTree *tree2 = [[BinarySearchTree alloc] init];
for (int i = 0; i < data2.count; i++) {
[tree2 add:data2[i]];
}
NSLog(@"%d",[tree isComplteBinaryTree]);
NSLog(@"%d",[tree1 isComplteBinaryTree]);
NSLog(@"%d",[tree2 isComplteBinaryTree]);
}- 运行结果
image.png
为了快速构建二叉树,可以将数组的元素按照层序遍历的顺序排列好
更多详细代码请看项目链接
本文会持续更新中,更多精彩内容敬请期待。
本文参考 MJ老师的 恋上数据结构与算法
本人技术水平有限,如有错误欢迎指正。
书写整理不易,您的打赏点赞是对我最大的支持和鼓励,欢迎点赞打赏。