问题
汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
递归算法

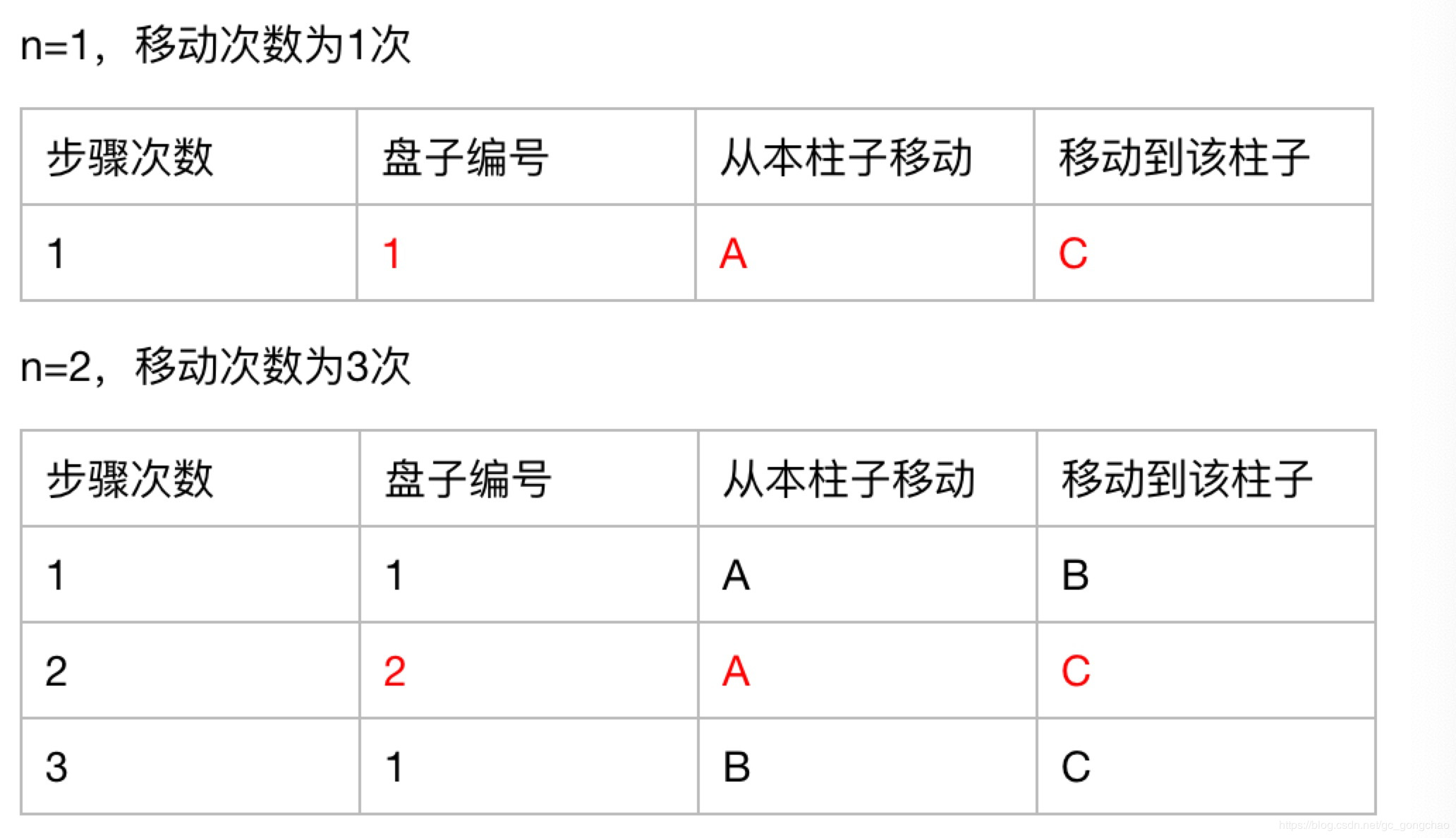
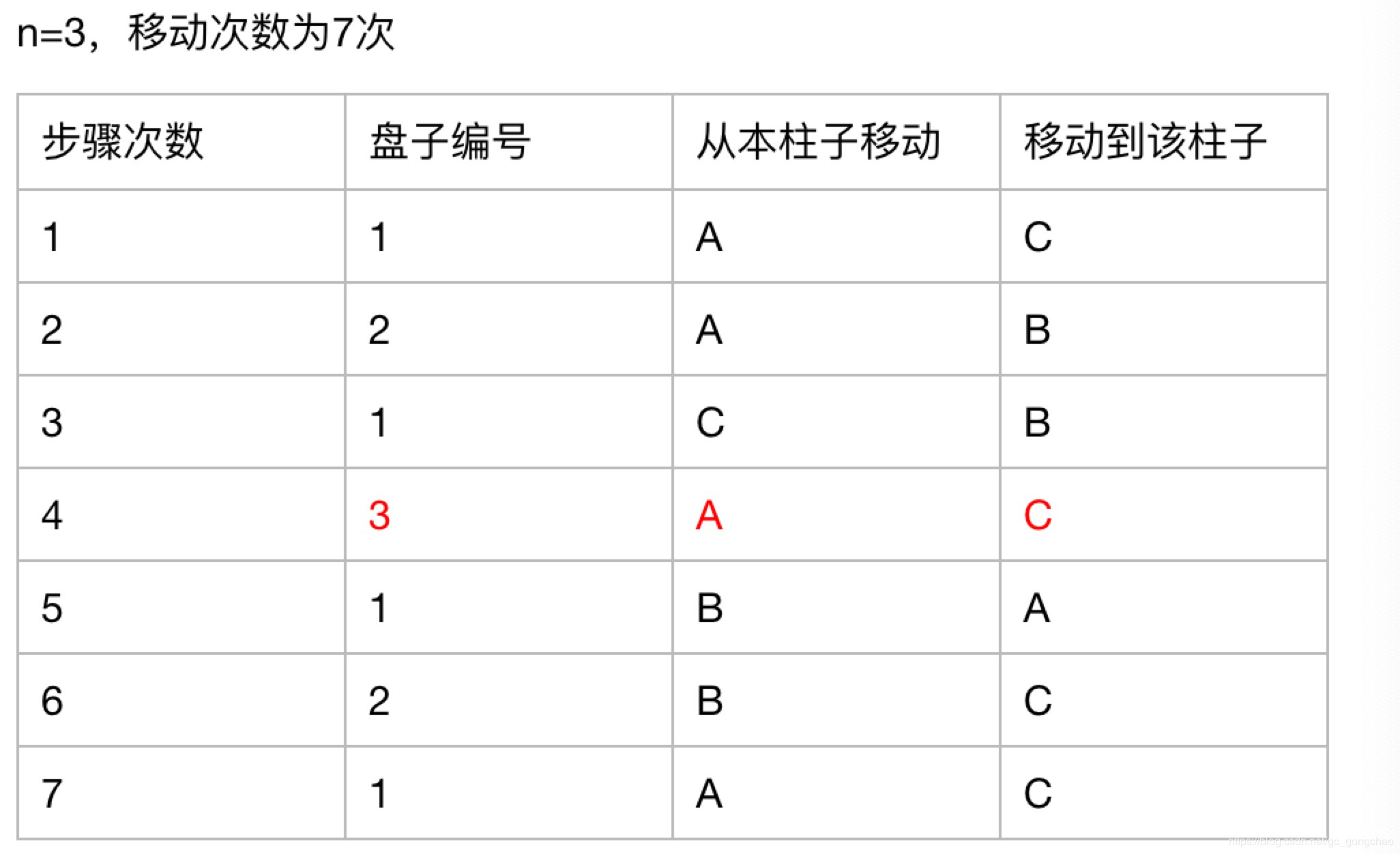
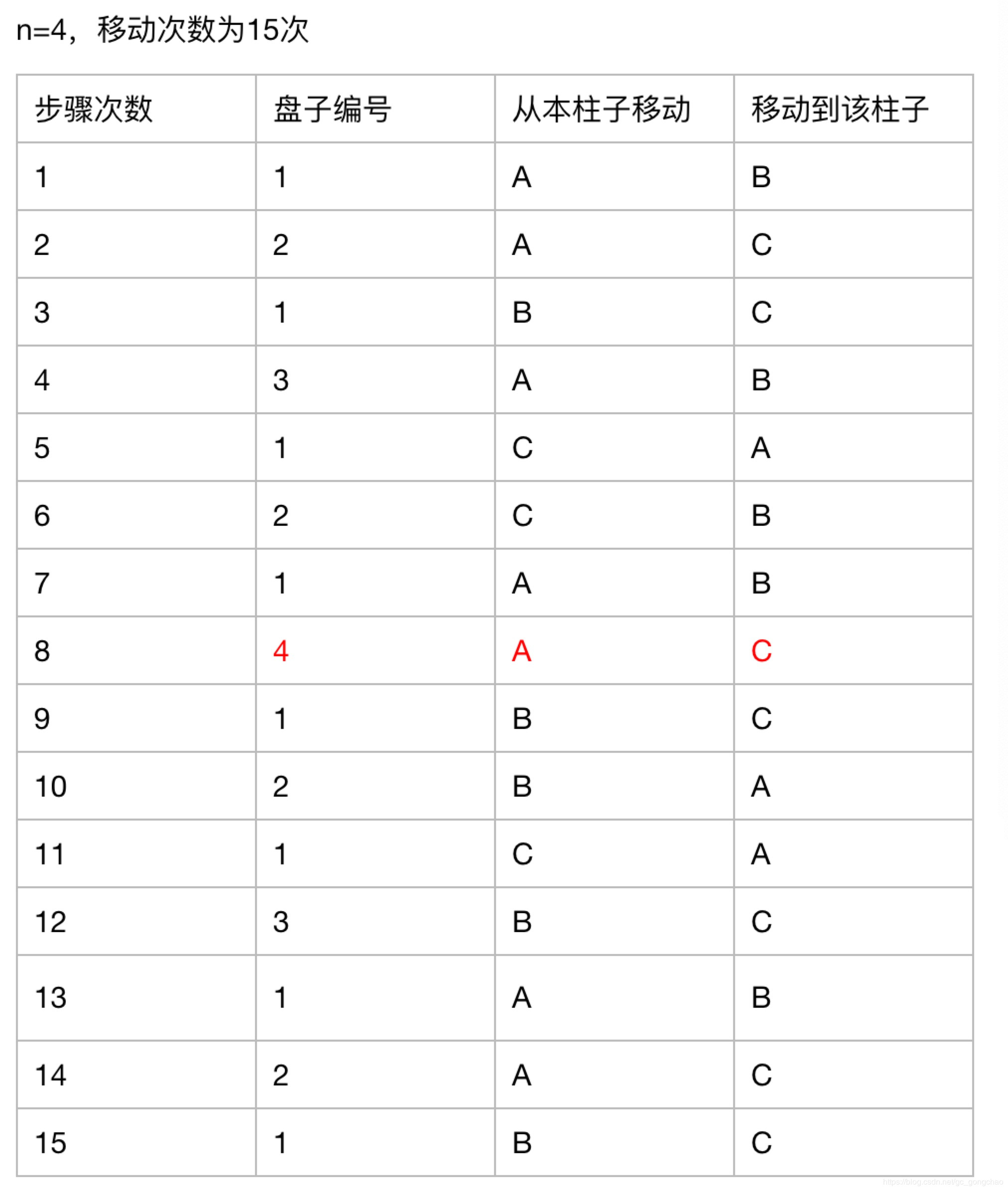
非递归算法
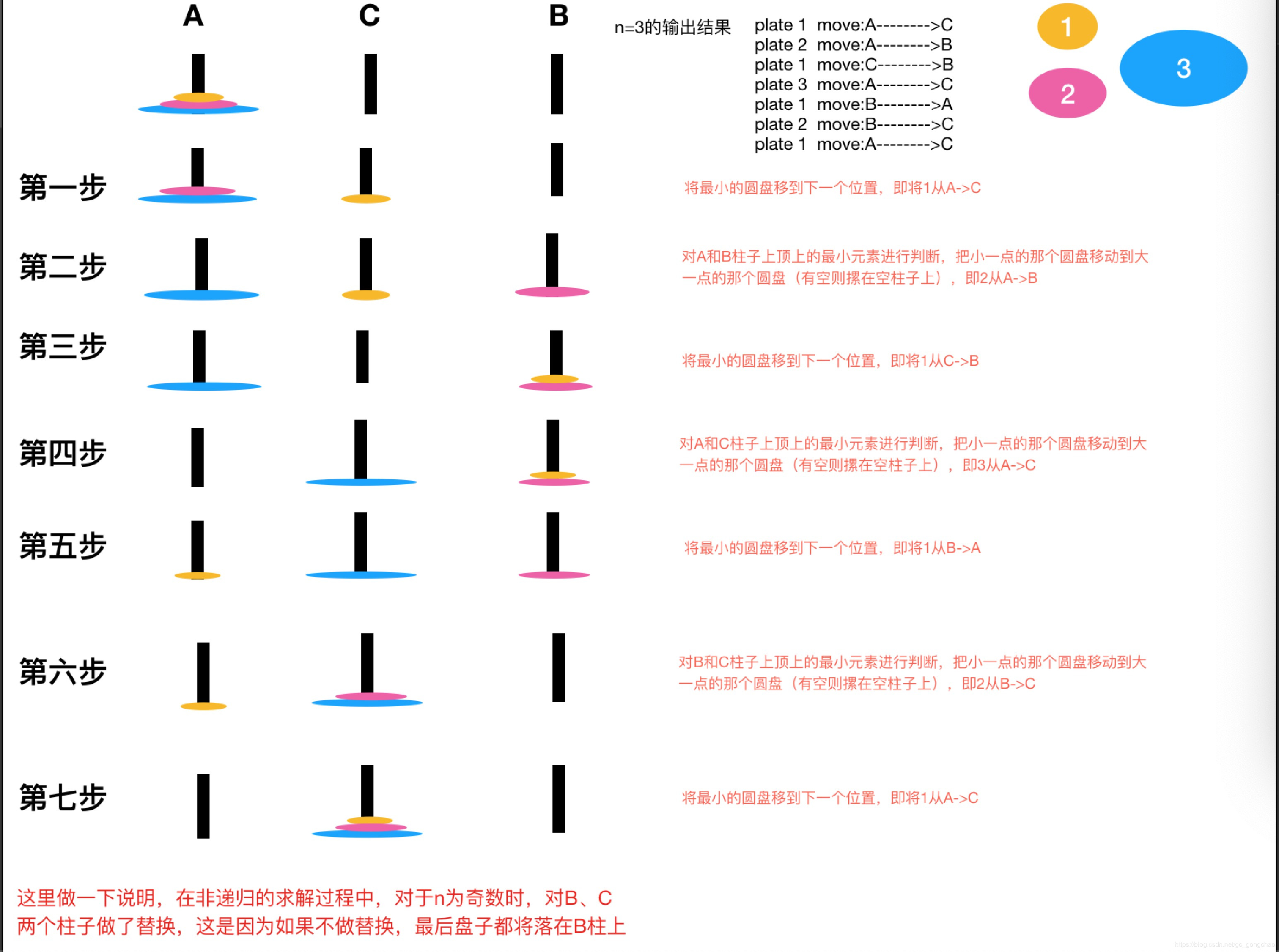
一个美国学者总结得到:所有的汉诺塔移动可以总结为重复的两步。 我们假设现在最小的圆盘在A柱子上,柱子为A,B,C 第一步:将最小圆盘移动到下一个柱子上,也就是B 第二步:对A柱子和C柱子进行顶上最小的元素进行判断,把小一点的那个圆盘移动到大一点的那个圆盘(有空则摞在空柱子上)。 重复上述两步就可以得到答案。注意:这样得到的最后的答案不一定是摞在C上,如果N是奇数将摞在B上,所以如果N是奇数我们就令第二个柱子为C,第三个柱子为B,这样就一定最后是摞在C上的。
为了形象地说明这个过程,下面以n=3时为例
实现代码
解决汉诺塔问题的算法代码如下:
package com.general.arithmetic.practice;
import java.util.ArrayList;
import java.util.Stack;
/***
* 汉诺塔问题的学习与练习
* 问题描述:从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有
* 一个原则:一次只能移动一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数。
*
* 汉诺塔的非递归算法:
* 一个美国学者总结得到:所有的汉诺塔移动可以总结为重复的两步,我们假设现在最小的圆盘在A柱子上,柱子A、B、C
* 第一步:将最小圆盘移动到下一个柱子上,也就是B
* 第二步:对A柱子和C柱子进行顶上最小的元素进行判断,把小一点的那个圆盘移动到大一点的那个圆盘(有空则放置在空柱子上)
* 重复上述两步就可以得到答案。
*
* **/
public class Hanoi {
public static int count=0;
public static Stack<Integer> plate=new Stack<Integer>();
public static int PLATE_COUNT=3;
public static ArrayList<Stack<Integer>> plate_array=new ArrayList<>();
public static char s[]={'A','B','C'};
public static void move_recursion(int n,char A,char C){
count++;
System.out.println("plate "+plate.search(n)+" move:"+A+"-------->"+C);
}
public static void hanoi_tower(int n,char A,char B,char C){
if(n==1){
move_recursion(1,A,C);
}else{
hanoi_tower(n-1,A,C,B);
move_recursion(n,A,C);
hanoi_tower(n-1,B,A,C);
}
}
public static boolean move(int before,int after){
if(plate_array.get(before).empty()){
return false;
}
if (!plate_array.get(after).empty()){
if((plate_array.get(after).peek()-plate_array.get(before).peek())<0){
return false;
}
}
plate_array.get(after).push(plate_array.get(before).peek());
;
System.out.println("plate "+ plate_array.get(before).pop()+" move:"+s[before]+"-------->"+s[after]);
return true;
}
public static void hanoi_tower(){
int count=0;
if(PLATE_COUNT%2==1){
s[1]='C';
s[2]='B';
}
while (true){
++count;
move((count - 1) % 3, (count) % 3 );
if (!move((count - 1) % 3 , (count + 1) % 3 )&&!move((count + 1) % 3, (count - 1) % 3 ))
break;
}
}
public static void main(String[] args){
if(plate.size()>0){
plate.clear();
}
for(int i=PLATE_COUNT;i>0;i--){
plate.push(i);
}
System.out.println("递归求移动汉诺塔的步骤:");
hanoi_tower(PLATE_COUNT,'A','B','C');
System.out.println("总共移动"+count+"次");
System.out.println("*********************");
System.out.println("非递归求移动汉诺塔的步骤");
for(int i=0;i<3;i++){
plate_array.add(new Stack<Integer>());
}
for(int i=PLATE_COUNT;i>0;i--){
plate_array.get(0).push(i);
}
hanoi_tower();
}
}
代码运行结果如下:
递归求移动汉诺塔的步骤:
plate 1 move:A-------->C
plate 2 move:A-------->B
plate 1 move:C-------->B
plate 3 move:A-------->C
plate 1 move:B-------->A
plate 2 move:B-------->C
plate 1 move:A-------->C
总共移动7次
*********************
非递归求移动汉诺塔的步骤
plate 1 move:A-------->C
plate 2 move:A-------->B
plate 1 move:C-------->B
plate 3 move:A-------->C
plate 1 move:B-------->A
plate 2 move:B-------->C
plate 1 move:A-------->C
参考链接:
blog.csdn.net/qq_19446965…
blog.csdn.net/yhf_naive/a…
转载请注明出处,谢谢合作!如果喜欢此文章不妨点个赞,也可以来下关注。