Live each day like it could be your last.
把每天都当作生命的最后一天,认真生活。
引言
大道至简,我的理想是用最简单的代码实现最美的算法。字符串匹配的应用非常广泛,java的indexOf(),js的全家桶一套匹配(find,indexOf,include...)等等。本文主要分享了它们底层依赖的字符串匹配算法。两种简单,两种复杂。话不多说,所有源码均已上传至github:链接
ps:BF算法是字符串匹配算法里最简单的了,需要做到知其然并知其所以然。RK算法理解是BF + HASH。至于后面的BM和KMP,能做到看懂理解其原理就行,前辈们已经造好了轮子,在需要的时候能想到用即可,尬写出来有不少难度。
BF算法
bf算法俗称朴素匹配算法,为什么叫这个名字呢,因为很暴力,在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。
解析
在这里i循环是跟踪主串txt,j是跟踪模式串pattern,首先外围先确定访问次数,tLen-pLen。
j循环来进行比较,这里可能唯一比较不好理解的是i + j,查看测试结果,应该可以明白。
private int bfSearch(String txt, String pattern) {
int tLen = txt.length();
int pLen = pattern.length();
if (tLen < pLen) return -1;
for (int i = 0; i <= tLen - pLen; i++) {
int j = 0;
for (; j < pLen; j++) {
System.out.println(txt.charAt(i + j) + " -- " + pattern.charAt(j));
if (txt.charAt(i + j) != pattern.charAt(j)) break;
}
if (j == pLen) return i;
}
return -1;
}变体
bf算法还有一个变化,用到了显示回退的思想,i,j的作用和常规的一样,这里的i相当于常规的i+j,只不过当发现不匹配的时候,需要回退i和j这两个指针,j重新回到开头,i指向下一个字符。
private int bfSearchT(String txt, String pattern) {
int tLen = txt.length();
int i = 0;
int pLen = pattern.length();
int j = 0;
for (; i < tLen && j < pLen; i++) {
System.out.println(txt.charAt(i) + " -- " + pattern.charAt(j));
if (txt.charAt(i) == pattern.charAt(j)) {
++j;
} else {
i -= j;
j = 0;
}
}
if (j == pLen) {
System.out.println("end... i = " + i + ",plen = " + pLen);
return i - pLen;
}
return -1;
}测试代码
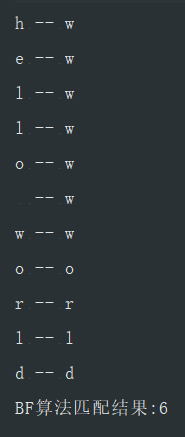
ps: hello world
public static void main(String[] args) {
BFArithmetic bf = new BFArithmetic();
String txt = "hello world";
String pattern = "world";
int res = bf.bfSearch(txt, pattern);
System.out.println("BF算法匹配结果:" + res);
// int resT = bf.bfSearchT(txt, pattern);
// System.out.println("BF算法(显示回退)匹配结果:" + resT);
}测试结果
RK算法
rk算法相当于bf算法的进阶版,它主要是引入了哈希算法。降低了时间复杂度。通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了。因为哈希值是一个数字,数字之间比较是否相等是非常快速的,所以模式串和子串比较的效率就提高了。
初始化
这里要把模式串预制进去,生成相对应的hash值,然后随机生成一个大素数,便于后续的使用。
private RKArithmetic(String pattern) {
this.pattern = pattern;
pLen = pattern.length();
aLen = 256;
slat = longRandomPrime();
System.out.println("随机素数:" + slat);
aps = 1;
// aLen^(pLen - 1) % slat
for (int i = 1; i <= pLen - 1; i++) {
aps = (aLen * aps) % slat;
}
patHash = hash(pattern, pLen);
System.out.println("patHash = " + patHash);
}准备
随机生成一个大素数
private static long longRandomPrime() {
BigInteger prime = BigInteger.probablePrime(31, new Random());
return prime.longValue();
}哈希算法
private long hash(String txt, int i) {
long h = 0;
for (int j = 0; j < i; j++) {
h = (aLen * h + txt.charAt(j)) % slat;
}
return h;
}校验字符串是否匹配
private boolean check(String txt, int i) {
for (int j = 0; j < pLen; j++)
if (pattern.charAt(j) != txt.charAt(i + j))
return false;
return true;
}实现
该实现还是比较容易阅读的,只不过将比较换成了hash值的比较。
private int rkSearch(String txt) {
int n = txt.length();
if (n < pLen) return -1;
long txtHash = hash(txt, pLen);
if ((patHash == txtHash) && check(txt, 0))
return 0;
for (int i = pLen; i < n; i++) {
txtHash = (txtHash + slat - aps * txt.charAt(i - pLen) % slat) % slat;
txtHash = (txtHash * aLen + txt.charAt(i)) % slat;
int offset = i - pLen + 1;
System.out.println("第" + offset + "次txtHash = " + txtHash);
if ((patHash == txtHash) && check(txt, offset))
return offset;
}
return -1;
}测试代码
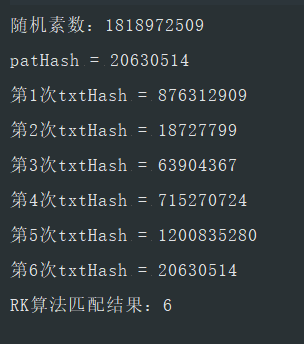
public static void main(String[] args) {
String pat = "world";
String txt = "hello world";
RKArithmetic searcher = new RKArithmetic(pat);
int res = searcher.rkSearch(txt);
System.out.println("RK算法匹配结果:" + res);
}测试结果
BM算法
BM算法的轮子已经造好。据说是最高效,最常用的字符串匹配算法。
分析
- 核心思想:是通过将模式串沿着主串大踏步的向后滑动,从而大大减少比较次数,降低时间复杂度。而算法的关键在于如何兼顾步子迈得足够大与无遗漏,同时要尽量提高执行效率。这就需要模式串在向后滑动时,遵守坏字符规则与好后缀规则,同时采用一些技巧。
- 坏字符规则:从后往前逐位比较模式串与主串的字符,当找到不匹配的坏字符时,记录模式串的下标值si,并找到坏字符在模式串中,位于下标si前的最近位置xi(若无则记为-1),si-xi即为向后滑动距离。(PS:我觉得加上xi必须在si前面,也就是比si小的条件,就不用担心计算出的距离为负了)。但是坏字符规则向后滑动的步幅还不够大,于是需要好后缀规则。
- 好后缀规则:从后往前逐位比较模式串与主串的字符,当出现坏字符时停止。若存在已匹配成功的子串{u},那么在模式串的{u}前面找到最近的{u},记作{u'}。再将模式串后移,使得模式串的{u'}与主串的{u}重叠。若不存在{u'},则直接把模式串移到主串的{u}后面。为了没有遗漏,需要找到最长的、能够跟模式串的前缀子串匹配的,好后缀的后缀子串(同时也是模式串的后缀子串)。然后把模式串向右移到其左边界,与这个好后缀的后缀子串在主串中的左边界对齐。
准备
构建坏字符哈希表
private void generateBC(char[] patChars, int[] records) {
for (int i = 0; i < aLen; i++) {
records[i] = -1;
}
for (int i = 0; i < patChars.length; i++) {
// 计算 b[i] 的 ASCII 值
int ascii = (int) patChars[i];
records[ascii] = i;
}
System.out.println("坏字符哈希表:");
print(records);
}好后缀
private void generateGS(char[] patChars, int[] suffix, boolean[] prefix) {
int pLen = patChars.length;
for (int i = 0; i < pLen; ++i) { // 初始化
suffix[i] = -1;
prefix[i] = false;
}
for (int i = 0; i < pLen - 1; ++i) {
int j = i;
// 公共后缀子串长度
int k = 0;
while (j >= 0 && patChars[j] == patChars[pLen - 1 - k]) {
--j;
++k;
//j+1 表示公共后缀子串在 patChars[0, i] 中的起始下标
suffix[k] = j + 1;
}
// 如果公共后缀子串也是模式串的前缀子串
if (j == -1) prefix[k] = true;
}
}移动
private int moveByGS(int index, int pLen, int[] suffix, boolean[] prefix) {
int k = pLen - 1 - index; // 好后缀长度
if (suffix[k] != -1) return index - suffix[k] + 1;
for (int i = index + 2; i <= pLen - 1; i++) {
if (prefix[pLen - i])
return i;
}
return -1;
}实现
- suffix 在模式串中,查找跟好后缀匹配的另一个子串
- prefix 记录模式串的后缀子串是否能匹配模式串的前缀子串
private int bmSearch(String txt, String pattern) {
// 记录模式串中每个字符最后出现的位置
int[] records = new int[aLen];
char[] txtChars = txt.toCharArray();
int tLen = txtChars.length;
char[] patChars = pattern.toCharArray();
int pLen = patChars.length;
generateBC(patChars, records);
int[] suffix = new int[pLen];
boolean[] prefix = new boolean[pLen];
generateGS(patChars, suffix, prefix);
//主串与模式串对齐的第一个字符
int index = 0;
while (index <= tLen - pLen) {
int i = pLen - 1;
// 模式串从后往前匹配
for (; i >= 0; --i) {
// 坏字符对应模式串中的下标是 i
if (txtChars[index + i] != patChars[i]) break;
}
if (i < 0) {
return index;
}
int x = i - records[(int) txtChars[index + i]];
int y = 0;
if (i < pLen - 1) {
y = moveByGS(i, pLen, suffix, prefix);
}
System.out.println("x = " + x + ",y = " + y);
index = index + Math.max(x, y);
}
return -1;
}测试代码
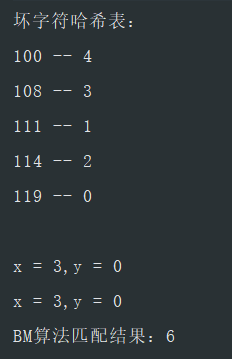
public static void main(String[] args) {
BMArithmetic bmArithmetic = new BMArithmetic();
String txt = "hello world";
String pattern = "world";
int res = bmArithmetic.bmSearch(txt, pattern);
System.out.println("BM算法匹配结果:" + res);
}
测试结果
BM启发式算法(精简版)
分析
BM算法不愧是号称线性级得计算,据说效率是KMP算法的3~4倍,有时间一定要验一下。
ps:遇到问题如果正着思考行不通,不妨反着考虑,新思想,get√。
初始化
private BoyerMoore(String pattern) {
this.pattern = pattern;
pLen = pattern.length();
int aLen = 256;
records = new int[aLen];
//初始化记录数组,默认-1
for (int i = 0; i < aLen; i++) {
records[i] = -1;
}
//模式串中的字符在其中出现的最右位置
for (int j = 0; j < pLen; j++) {
records[pattern.charAt(j)] = j;
}
}实现
根据命名skip也能分析出俩关键字倒序,跳跃性。
private int bmSearch(String txt) {
int tLen = txt.length();
int skip;
for (int i = 0; i <= tLen - pLen; i += skip) {
skip = 0;
for (int j = pLen - 1; j >= 0; --j) {
System.out.println(txt.charAt(i + j) + " -- " + pattern.charAt(j));
if (txt.charAt(i + j) != pattern.charAt(j)) {
skip = j - records[txt.charAt(i + j)];
if (skip < 1) skip = 1;
break;
}
}
if (skip == 0) return i;
}
return -1;
}测试代码
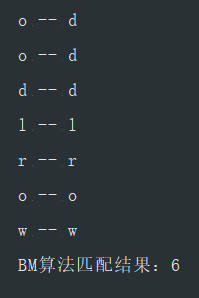
public static void main(String[] args) {
String txt = "hello world";
String pattern = "world";
BoyerMoore bm = new BoyerMoore(pattern);
int res = bm.bmSearch(txt);
System.out.println("BM算法匹配结果:" + res);
}测试结果
KMP算法
分析
kmp算法引入一个失效函数--next数组。这个算法的关键就在于next函数是如何计算出来的。妙不可言?不,是头皮发麻,难以理解。只能debug一步一步跟了。
准备
精髓:理解k = next[k]。因为前一个的最长串的下一个字符不与最后一个相等,需要找前一个的次长串,问题就变成了求0到next(k)的最长串,如果下个字符与最后一个不等,继续求次长串,也就是下一个next(k),直到找到,或者完全没有。
private int[] getNext(char[] patChars, int pLen) {
int[] next = new int[pLen];
next[0] = -1;
int k = -1;
for (int i = 1; i < pLen; i++) {
while (k != -1 && patChars[k + 1] != patChars[i]) {
k = next[k];
}
if (patChars[k + 1] == patChars[i])
++k;
next[i] = k;
}
System.out.println("好前缀:");
print(next);
return next;
}实现
private int kmpSearch(String txt, String pattern) {
char[] txtChars = txt.toCharArray();
int tLen = txtChars.length;
char[] patChars = pattern.toCharArray();
int pLen = patChars.length;
int[] next = getNext(patChars, pLen);
int index = 0;
for (int i = 0; i < tLen; i++) {
while (index > 0 && txtChars[i] != patChars[index]) {
index = next[index - 1] + 1;
}
System.out.println(txtChars[i] + " -- " + patChars[index]);
if (txtChars[i] == patChars[index])
++index;
if (index == pLen)
return i - pLen + 1;
}
return -1;
}测试代码
public static void main(String[] args) {
KMPArithmetic kmpArithmetic = new KMPArithmetic();
String txt = "hello world";
String pattern = "world";
int res = kmpArithmetic.kmpSearch(txt, pattern);
System.out.println("KMP算法匹配结果:" + res);
}测试结果
KMP算法(基于确定优先状态自动机dfa)
初始化
private KMPByDFA(String pattern) {
this.pattern = pattern;
this.pLen = pattern.length();
int aLen = 256;
dfa = new int[aLen][pLen];
dfa[pattern.charAt(0)][0] = 1;
int i = 0;
for (int j = 1; j < pLen; j++) {
for (int k = 0; k < aLen; k++) {
//复制匹配失败情况下的值
dfa[k][j] = dfa[k][i];
}
//设置匹配成功情况下的值
dfa[pattern.charAt(j)][j] = j + 1;
//更新重新状态
i = dfa[pattern.charAt(j)][i];
}
}实现
private int kmpSearch(String txt) {
int i = 0;
int j = 0;
int tLen = txt.length();
for (; i < tLen && j < pLen; i++) {
j = dfa[txt.charAt(i)][j];
}
//找到匹配,到达模式串的结尾
if (j == pLen)
return i - pLen;
return -1;
}测试代码
public static void main(String[] args) {
String txt = "hello world";
String pattern = "world";
KMPByDFA kmp = new KMPByDFA(pattern);
int res = kmp.kmpSearch(txt);
System.out.println("BM算法匹配结果:" + res);
}测试结果

end

您的点赞和关注是对我最大的支持,谢谢!