mAP是mean of Average Precision的缩写,意思是平均精确度(average precision)的平均(mean),是object detection中模型性能的衡量标准。object detection中,因为有物体定位框,分类中的accuracy并不适用,因此才提出了object detection独有的mAP指标,但这也导致mAP没有分类中的accuracy那么直观。但也没有那么复杂,本文将详细解释mAP的计算方法。首先,简单回顾几个基础概念。
查准率(Precision)和查全率(recall)
查准率(Precision)是指在所有预测为正例中真正例的比率,也即预测的准确性。 查全率(Recall)是指在所有正例中被正确预测的比率,也即预测正确的覆盖率。 一个样本模型预测按正确与否分类如下:

则,查准率和查全率计算公式:

交并比IoU(Intersection over union)
交并比IoU衡量的是两个区域的重叠程度,是两个区域重叠部分面积占二者总面积(重叠部分只计算一次)的比例。如下图,两个矩形框的IoU是交叉面积(中间图片红色部分)与合并面积(右图红色部分)面积之比。
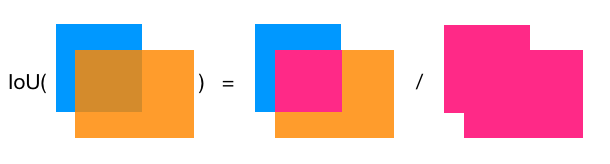
这里需要注意的是IoU=0.5,并不意味着每个框刚好有50%与另外一个框交叉部分,而是每个框大约有2/3被交叉。有点反直觉。
我当初看到IoU,非常疑惑为啥不按交叉面积占每个框的比例(也即IoA Intersection over Area)取大值计算重叠度,更符合直觉。其实这种算法只反应小图片的被遮盖度,并不能反映互相之间的重叠度,一般情况下不可取。如下图,橙色部分较小,IoA很大,但对于蓝色部分,IoA就很小,只按橙色取IoA显然有失偏驳。

单类别AP(Average Precision)的计算
物体检测中的每一个预测结果包含两部分,预测框(bounding box)和置信概率(Pc)。bounding box通常以矩形预测框的左上角和右下角的坐标表示,即x_min, y_min, x_max, y_max,如下图。置信概率Pc有两层意思,一是所预测bounding box的类别,二是这个类别的置信概率,如下图中的P_dog=0.88,代表预测绿色框为dog,并且置信概率为88%。

那么,怎么才叫预测正确呢?显而易见的,必须满足两个条件:
- 类别正确且置信度大于一定阀值(P_threshold)
- 预测框与真实框(ground truth)的IoU大于一定阀值(IoU_threshold) 如下图,假如P_threshold=0.6,IoU_threshold=0.5,则绿色框预测正确,记为True Positive。

而在衡量模型性能时,IoU_threshold先取一个定值,然后综合考虑各种P_threshold取值时的性能,进而得到一个与P_threshold选定无关的模型性能衡量标准。
AP是计算单类别的模型平均准确度。
假如目标类别为Dog,测试了5张照片后,得到了Dog的10个预测结果,选定IoU_threshold=0.5,然后按confidence从高到低排序,如下(BB表示BoundingBox序号,IoU>=0.5时GT=1):
Rank | BB | confidence | GT
----------------------------
1 | BB1 | 0.9 | 1
----------------------------
2 | BB2 | 0.8 | 1
----------------------------
3 | BB1 | 0.8 | 1
----------------------------
4 | BB3 | 0.5 | 0
----------------------------
5 | BB4 | 0.4 | 0
----------------------------
6 | BB5 | 0.4 | 1
----------------------------
7 | BB6 | 0.3 | 0
----------------------------
8 | BB7 | 0.2 | 0
----------------------------
9 | BB8 | 0.1 | 1
----------------------------
10 | BB9 | 0.1 | 1
----------------------------
因此,我们有 TP=5 (BB1, BB2, BB5, BB8, BB9),FP=5 (重复检测到的BB1也算FP)。除了表里检测到的5个GT以外,我们还有2个GT没被检测到,因此: FN = 2,GT=7.
然后依次从上到下设定对应的rank为正反分界线,此rank之前(包含此rank)的预测为正,此rank之后的预测为反,然后计算对应的Precision和Recall:
rank=1 precision=1.00 and recall=0.14
--------------------------------------
rank=2 precision=1.00 and recall=0.29
--------------------------------------
rank=3 precision=0.66 and recall=0.29
--------------------------------------
rank=4 precision=0.50 and recall=0.29
--------------------------------------
rank=5 precision=0.40 and recall=0.29
--------------------------------------
rank=6 precision=0.50 and recall=0.43
--------------------------------------
rank=7 precision=0.43 and recall=0.43
--------------------------------------
rank=8 precision=0.38 and recall=0.43
--------------------------------------
rank=9 precision=0.44 and recall=0.57
--------------------------------------
rank=10 precision=0.50 and recall=0.71
--------------------------------------
比如rank=4时,TP=2 (BB1, BB2),则
Precision=2/4=0.5,Recall=TP/GT=2/7=0.29
可以看出,随着预测正反分割线的向下移动,Recall稳步变大,Precision整体减小,局部上下跳动,PR曲线如下图:

AP(Average Precision)的计算基本等同于计算PR曲线下的面积,但略有不同。需要先将PR曲线平滑化。
方法是,查全率r对应的查准率p,取查全率大于等于r时最大的查准率p。即,

平滑后的曲线如下图中的绿色曲线:
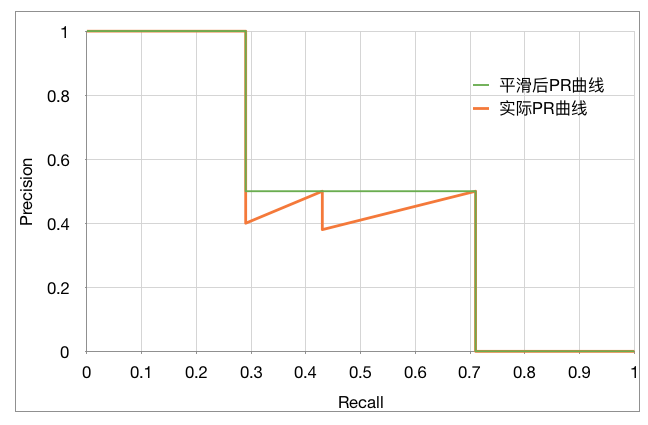
对于AP(Average Precision)的计算有两种方法:
- VOC2010之前的方法
AP =(平滑后PR曲线上,Recall分别等于0,0.1,0.2,… , 1.0等11处Precision的平均值)。

这里则有:
AP=(1 + 1 + 1 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0 + 0 + 0) / 11 = 0.5
- VOC2010及以后的方法
AP=平滑后PR曲线下包围的面积 这里则有:
AP = (0.14-0) * 1 + (0.29-0.14) * 1 + (0.43-0.29) * 0.5 + (0.57-0.43) * 0.5 + (0.71-0.57) * 0.5 + (1-0.71) * 0 = 0.5
这里两种方案得出的AP值相同,但通常是不同的。
需要注意的是上述AP的计算并没有显式设定P_threshold,而是通过从上到下依次指定每一个rank为正反分界线来变相的反映P_threshold不同取值。
mAP的计算
上述计算的AP只是针对dog这个类别,物体检测通常有多个类别,模型性能肯定是多个类别准度的综合度量。
- VOC数据集中的mAP VOC数据集中的mAP计算的是IoU_threshold=0.5时各个类别AP的均值。
- COCO数据集中的mAP 检测是否正确有两个超参数,P_threshold和IoU_threshold。AP是固定了IoU_threshold,再综合考虑各个P_threshold下的模型平均准确度。 VOC认为IoU_threshold固定一个单值0.5即可,COCO则认为固定了IoU_threshold的取值,无法衡量IoU_threshold对模型性能的影响。
比如, A模型在IoU_threshold=0.5时,mAP=0.4。 B模型在IoU_threshold=0.7时,mAP同样为0.4。 依据VOC的标准,AB模型的性能一样,但显然B模型的框更准,性能更优。 COCO在VOC标准的基础上,取IoU_threshold=0.5,0.55, 0.6,… , 0.95时各个mAP的均值。
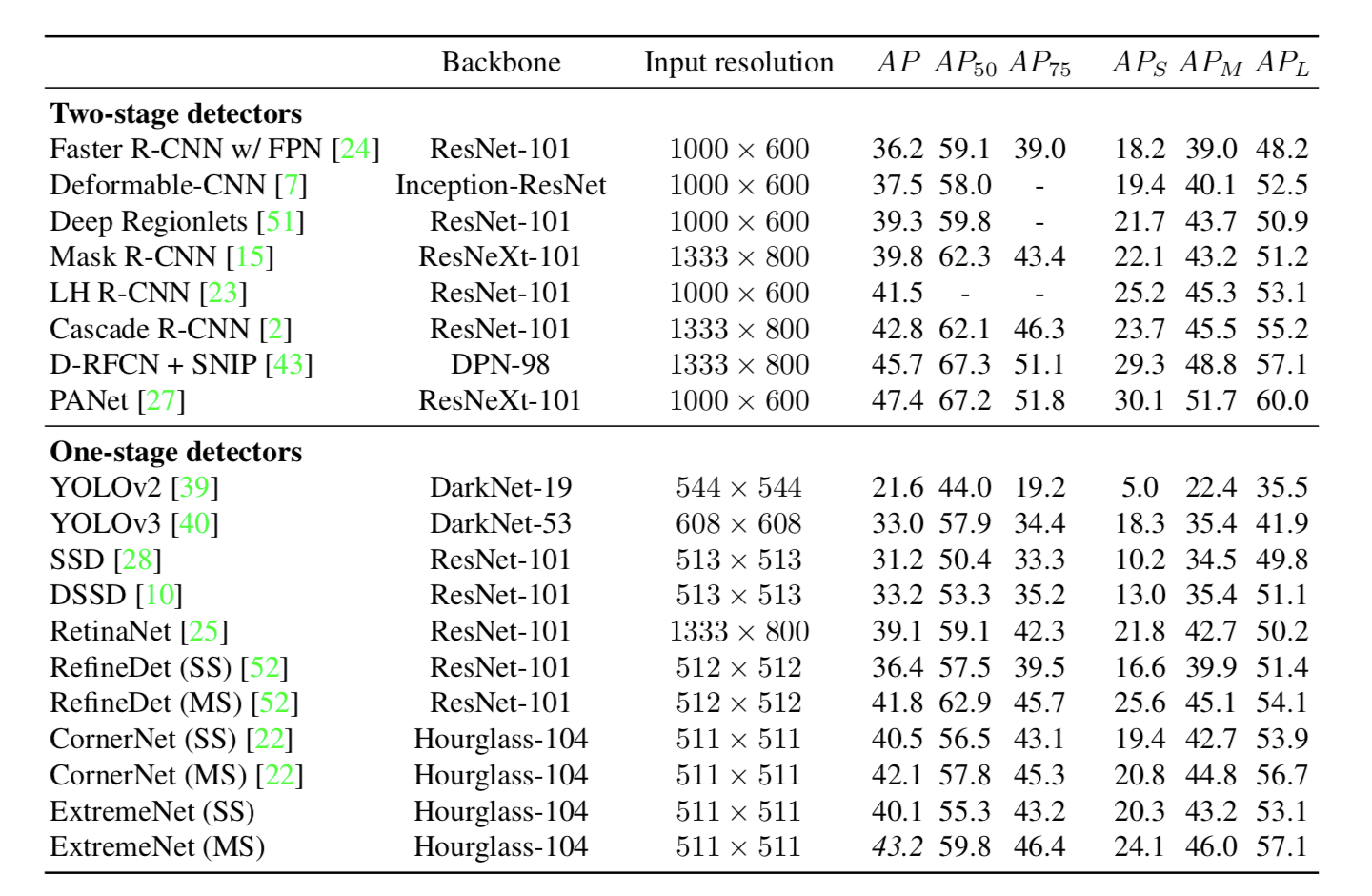
下图给出了当前mAP最佳结果。
mAP的不足
mAP虽然综合考虑了P_threshold和IoU_threshold各个取值时的平均模型准确度,使得模型优劣的评判标准不随P_threshold和IoU_threshold取值变化而变化,但在工程应用中,物体是否被正确检测到,还是需要具体的P_threshold和IoU_threshold,工程上更关心在固定的P_threshold和IoU_threshold下的准确率。这就需要我们自己实现与具体应用相符的评判标准。

参考文章