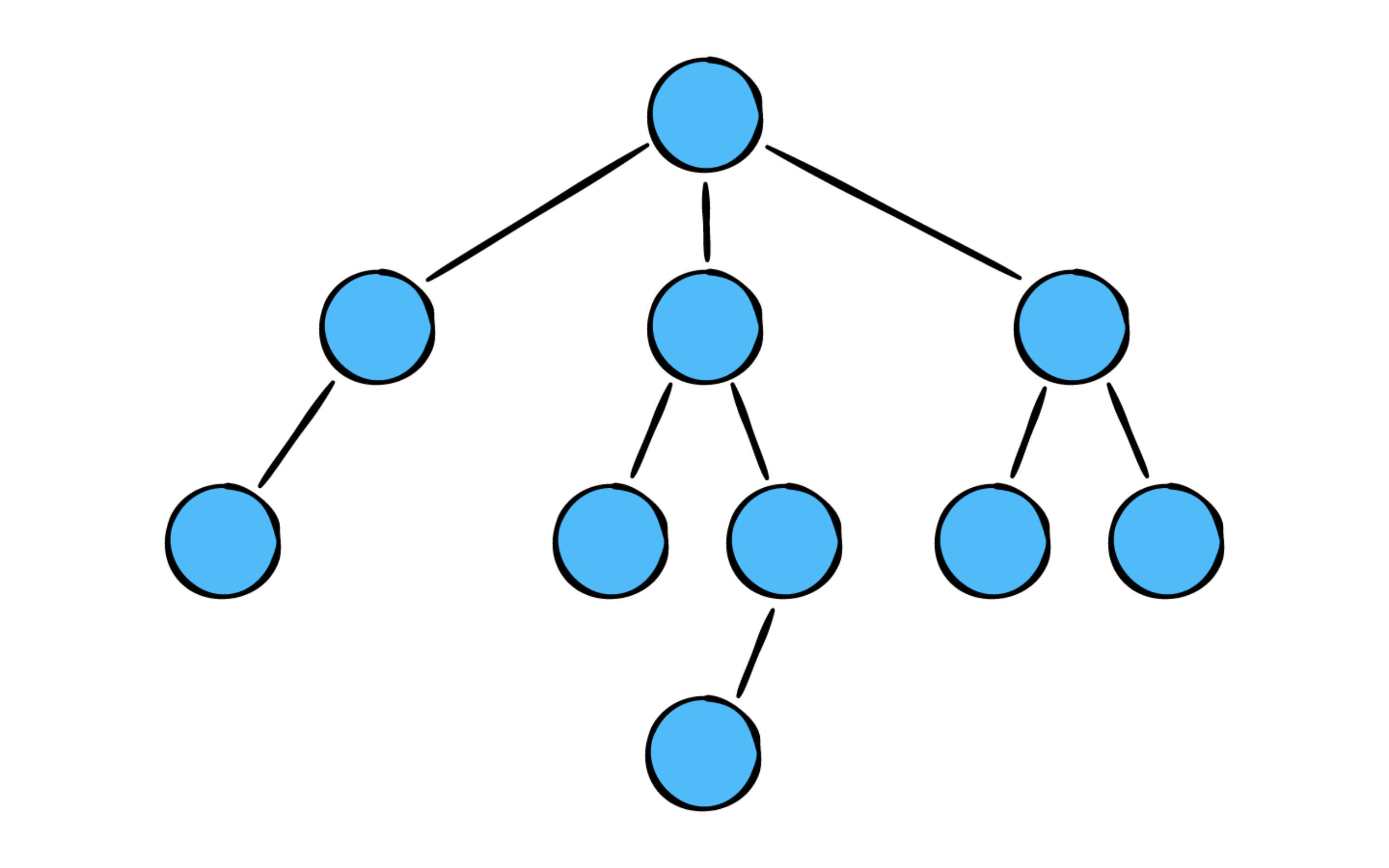
树型数据结构非常重要。它能解决很多的计算机开发问题，比如：

• 代表数据的层级关系。
• 管理排序好的数据。
• 提高快速查找操作效率。

树型数据结构有很多种类型，这里我们先简单看看它的基本实现。

下面为了方便把树型数据结构 称为 树结构。

• 一些需要了解的术语

• Node（节点）

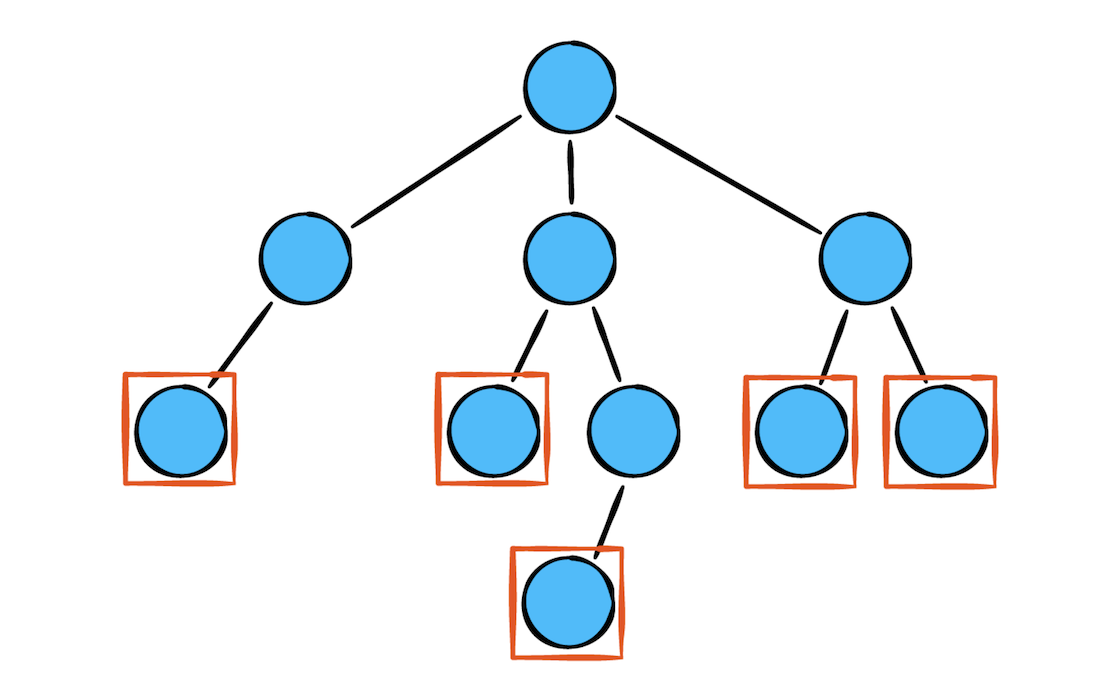
就像是链表一样，树结构也是由节点组成的。如图所示：

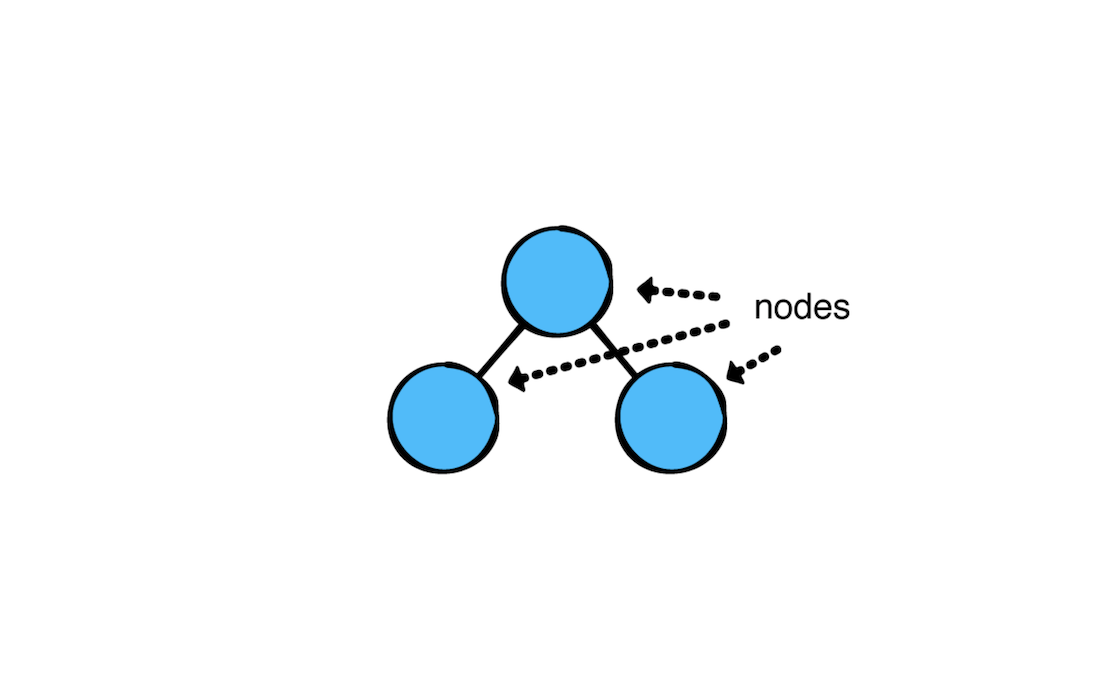
每个节点都有一个自己的值也可以包含一些子节点。

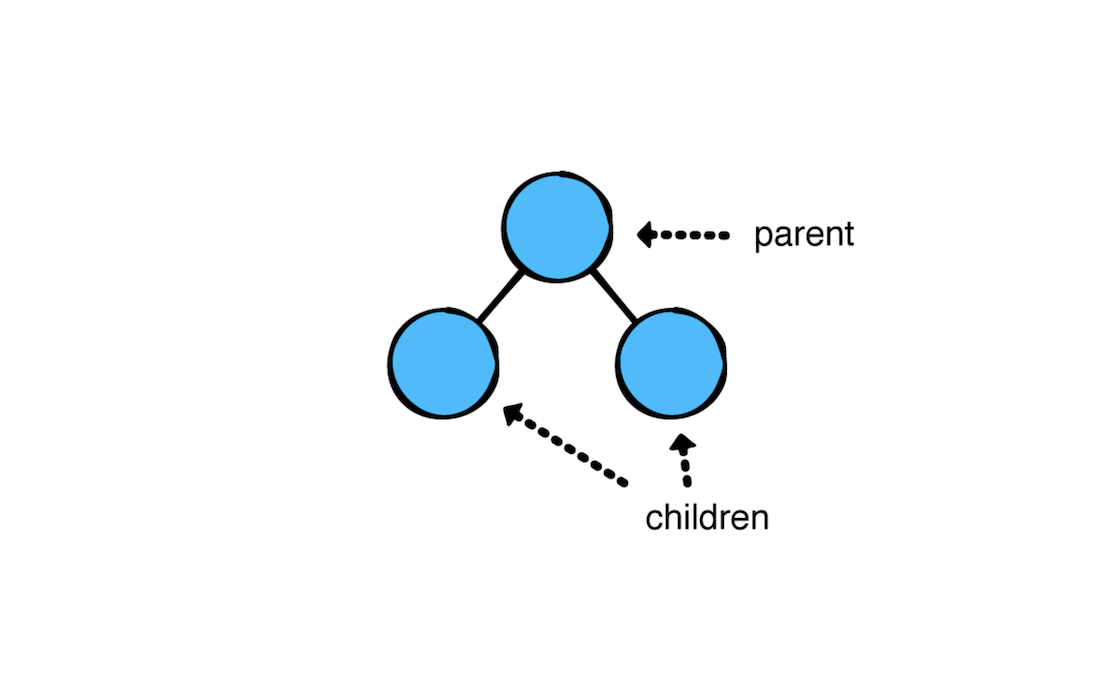
• Parent child（父节点和子节点）

• Root（根节点）

根节点没有父节点

• Leaf（叶子节点）

叶子节点没有子节点

• 实现

添加基本实现：

public class TreeNode<T> {
    // 节点包含的值
    var value: T
    
    // 可能的子节点
    var children: [TreeNode] = []
    
    // 初始化设置自己节点包含的值
    public init(_ value: T) {
        self.value = value
    }
    
    // 添加子节点
    func add(_ child: TreeNode) {
        children.append(child)
    }
}

添加一个辅助方法：

public func example(of description: String, action: () -> Void) {
    print("---Example of: \(description)---")
    action()
    print()
}

测试：

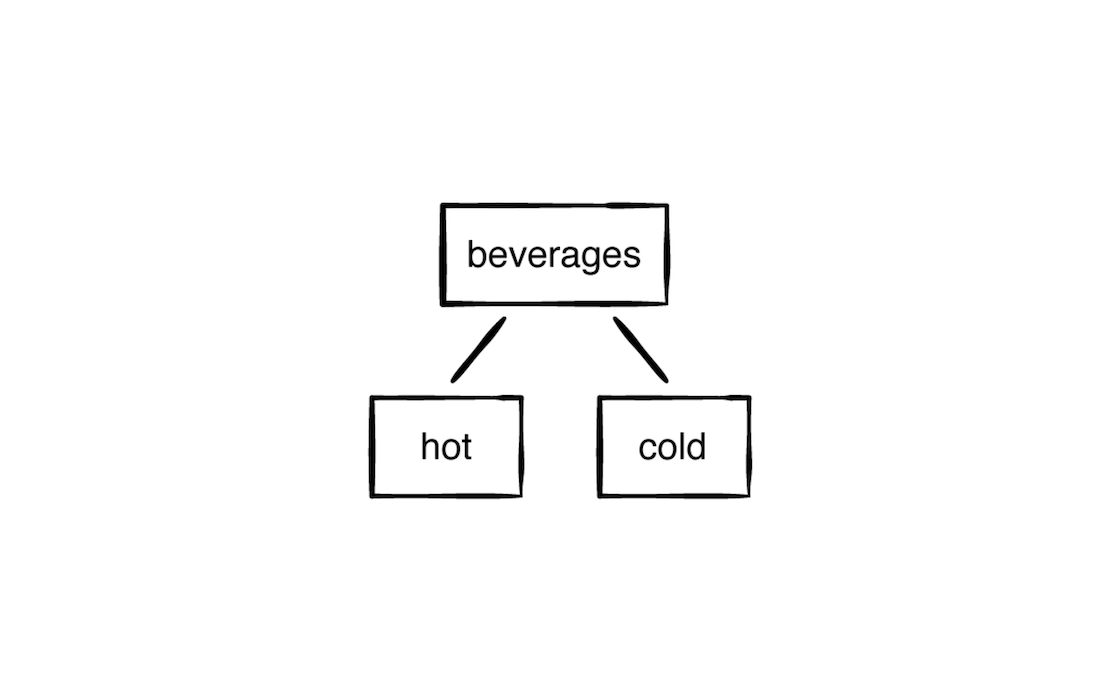
example(of: "creating a tree") {
    let tree = TreeNode("Beverages")
    let hot = TreeNode("Hot")
    let code = TreeNode("Cold")
    tree.add(hot)
    tree.add(code)
}

此时它的层级结构是这样的：

• 节点的遍历算法

在链表和数组中，里面数据的遍历是简单明了的，只需要从数据的开始遍历到结尾就好了。

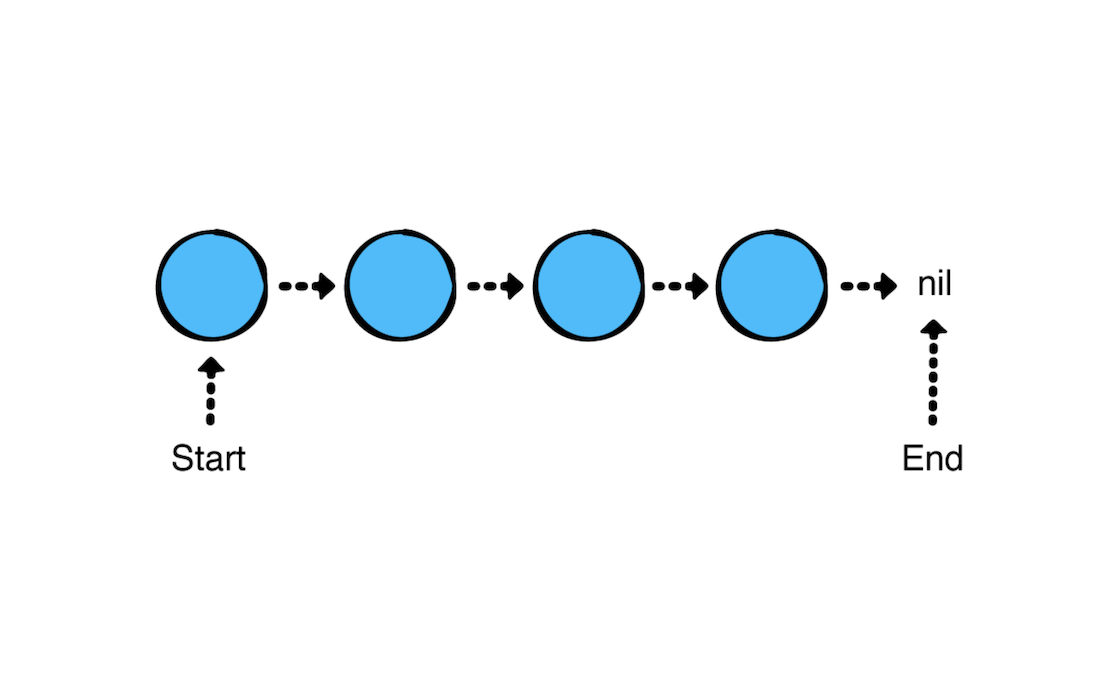
但是树结构有点不一样。

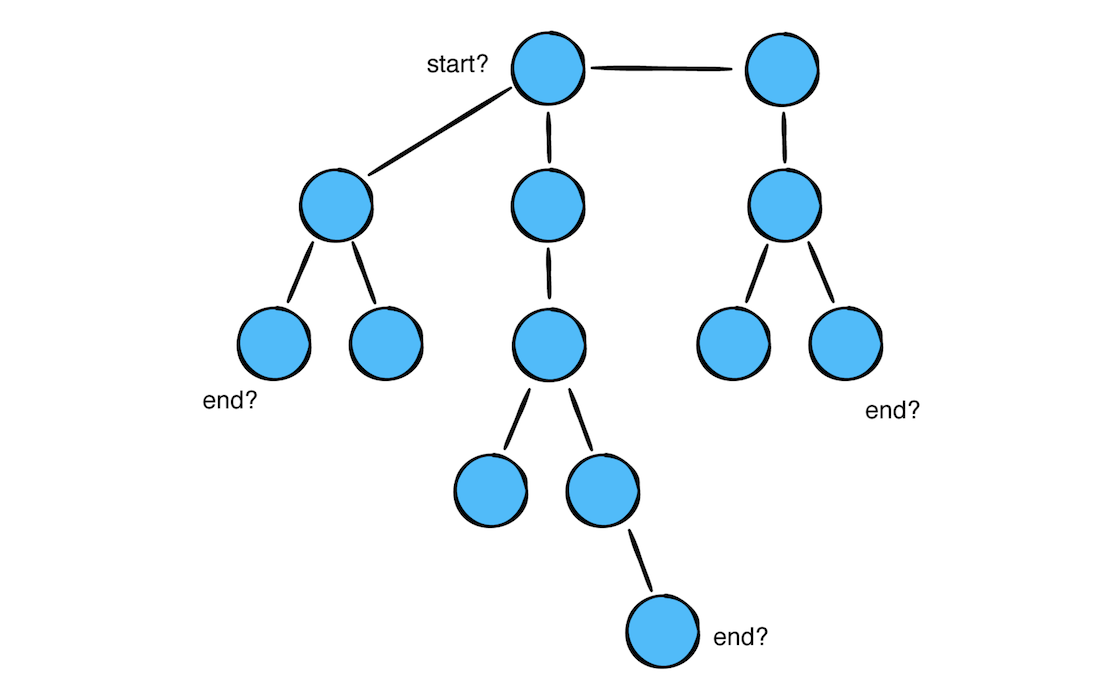
对于树结构 我们可以使用 深度优先 和 广度优先 方式遍历

• 深度优先遍历

实现方法：

extension TreeNode {

    func forEachDepthFirst(visit: (TreeNode) -> Void) {
        // 先处理自己
        visit(self)
        
        // 遍历自己的每个子节点
        children.forEach { $0.forEachDepthFirst(visit: visit) }
    }
        
}

深度优先的思想主要是先处理自己的信息，然后遍历子节点，子节点再递归遍历自己。

添加测试辅助：

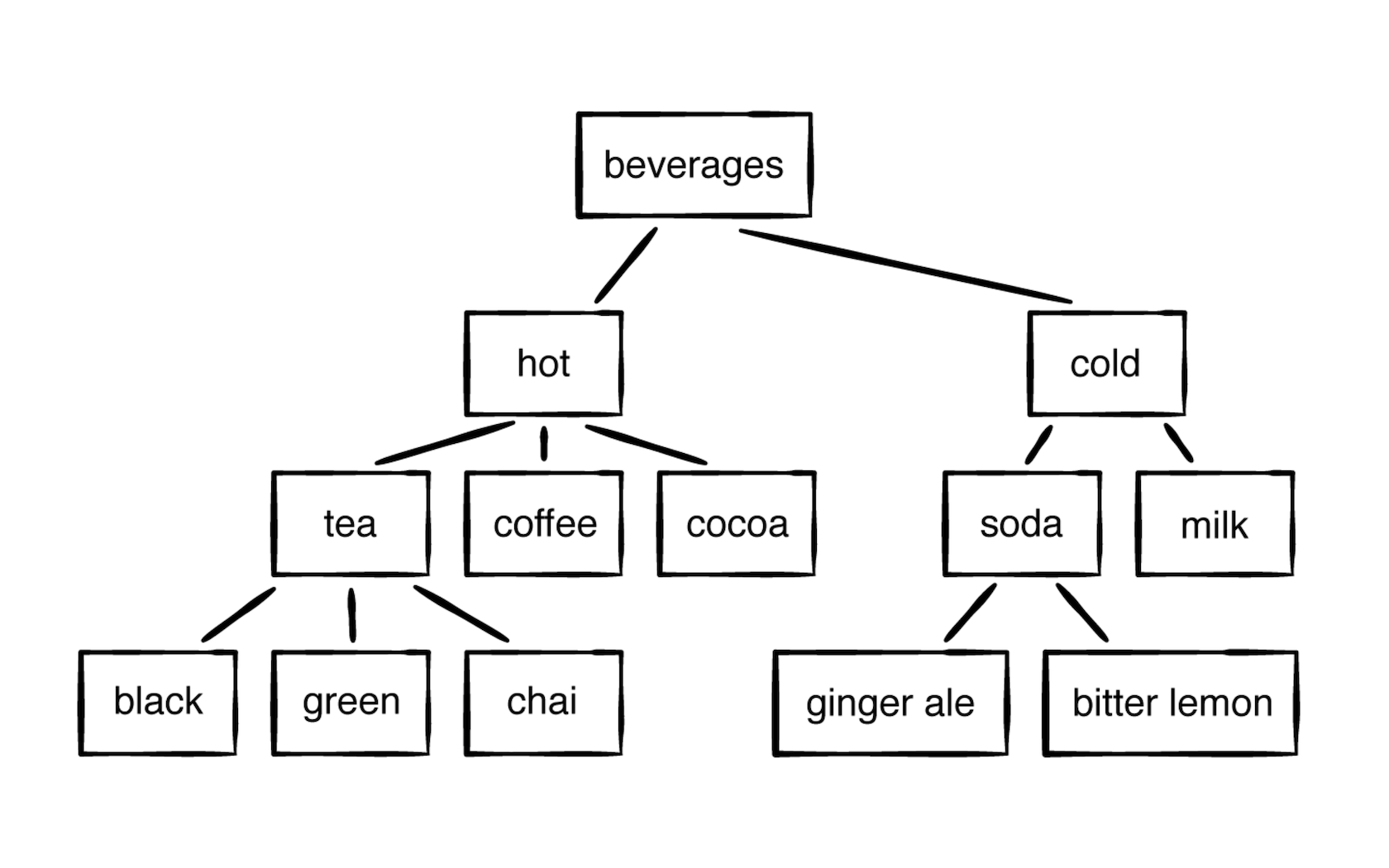
    func makeBeverageTree() -> TreeNode<String> {
        let tree = TreeNode("Beverages")
        
        let hot = TreeNode("hot")
        let cold = TreeNode("cold")
        
        let tea = TreeNode("tea")
        let coffee = TreeNode("coffee")
        let chocolate = TreeNode("cocoa")
        
        let blackTea = TreeNode("black")
        let greenTea = TreeNode("green")
        let chaiTea = TreeNode("chai")
        
        let soda = TreeNode("soda")
        let milk = TreeNode("milk")
        
        let gingerAle = TreeNode("ginger ale")
        let bitterLemon = TreeNode("bitter lemon")
        
        tree.add(hot)
        tree.add(cold)
        
        hot.add(tea)
        hot.add(coffee)
        hot.add(chocolate)
        
        cold.add(soda)
        cold.add(milk)
        
        tea.add(blackTea)
        tea.add(greenTea)
        tea.add(chaiTea)
        
        soda.add(gingerAle)
        soda.add(bitterLemon)
        
        return tree
    }

方法主要是返回一个树结构，如图所示：

测试：

example(of: "depth-first-travesal") {
    let tree = makeBeverageTree()
    tree.forEachDepthFirst { print($0.value) }
}

输出：

---Example of: depth-first-travesal---
Beverages
hot
tea
black
green
chai
coffee
cocoa
cold
soda
ginger ale
bitter lemon
milk

• 广度优先遍历

实现方法：

extension TreeNode {
    
    func forEachLevelOrder(visit: (TreeNode) -> Void) {
        // 先处理自己
        visit(self)
        
        // 使用一个队列结构作为节点的存储
        var queue = Queue<TreeNode>()
        
        // 这个是关键，把每一个节点的子节点添加到队列里面
        children.forEach { queue.enqueue($0) }
        
        // 出队处理
        while let node = queue.dequeue() {
            visit(node)
            
            // 再次把每个当前节点的所有子节点添加到队列里面
            node.children.forEach { queue.enqueue($0) }
        }
    }
    
}

在这里实现广度优先遍历的关键是使用了一个队列数据结构作为节点的存储。队列是先进先出的数据结构 队列数据结构

这里使用的队列结构的实现如下：

public struct Queue<T> {
    
    private var leftStack: [T] = []
    private var rightStack: [T] = []
    
    public init() {}
    
    public var isEmpty: Bool {
        leftStack.isEmpty && rightStack.isEmpty
    }
    
    public var peek: T? {
        !leftStack.isEmpty ? leftStack.last : rightStack.first
    }
    
    @discardableResult public mutating func enqueue(_ element: T) -> Bool {
        rightStack.append(element)
        return true
    }
    
    public mutating func dequeue() -> T? {
        if leftStack.isEmpty {
            leftStack = rightStack.reversed()
            rightStack.removeAll()
        }
        return leftStack.popLast()
    }
    
}

测试：

example(of: "level-order-travesal") {
    let tree = makeBeverageTree()
    tree.forEachLevelOrder { print($0.value) }
}

输出：

---Example of: level-order-travesal---
Beverages
hot
cold
tea
coffee
cocoa
soda
milk
black
green
chai
ginger ale
bitter lemon

• 搜索功能

实现方法：

extension TreeNode where T: Equatable {
    func search(_ value: T) -> TreeNode? {
        var result: TreeNode?
        forEachLevelOrder { (node) in
            if node.value == value {
                result = node
            }
        }
        return result
    }
}

这里就直接使用了上面的广度优先的遍历方式实现节点的搜索了。搜索功能不同的实现方式输出的结果有时候是会不一样的。在上面的搜索实现中，如果有重复的节点数据，那么后面一个节点会覆盖前面的节点。

测试：

example(of: "searching for a node") {
    let tree = makeBeverageTree()
    
    if let search1 = tree.search("ginger ale") {
        print("Found node: \(search1)")
    }
    
    if let search1 = tree.search("WKD Blue") {
        print("Found node: \(search1)")
    } else {
        print("Couldn't find: WKD Blue")
    }
}

输出：

---Example of: searching for a node---
Found node: Trees.TreeNode<Swift.String>
Couldn't find: WKD Blue

• 要点

• 树结构 和链表数据结构比较相似。但是链表一个节点一般只能指向下一个节点，而树的一个节点可以有多个子节点。

• 树结构里面除了根节点没有父节点，其它节点都有一个父节点。

• 叶子节点没有子节点。

• 所有的树结构类型的都可以深度优先遍历和广度优先遍历，只不过不同类型的树结构 遍历方法的内部实现会有点小区别而已。

• 试题

有下面一个简单树：

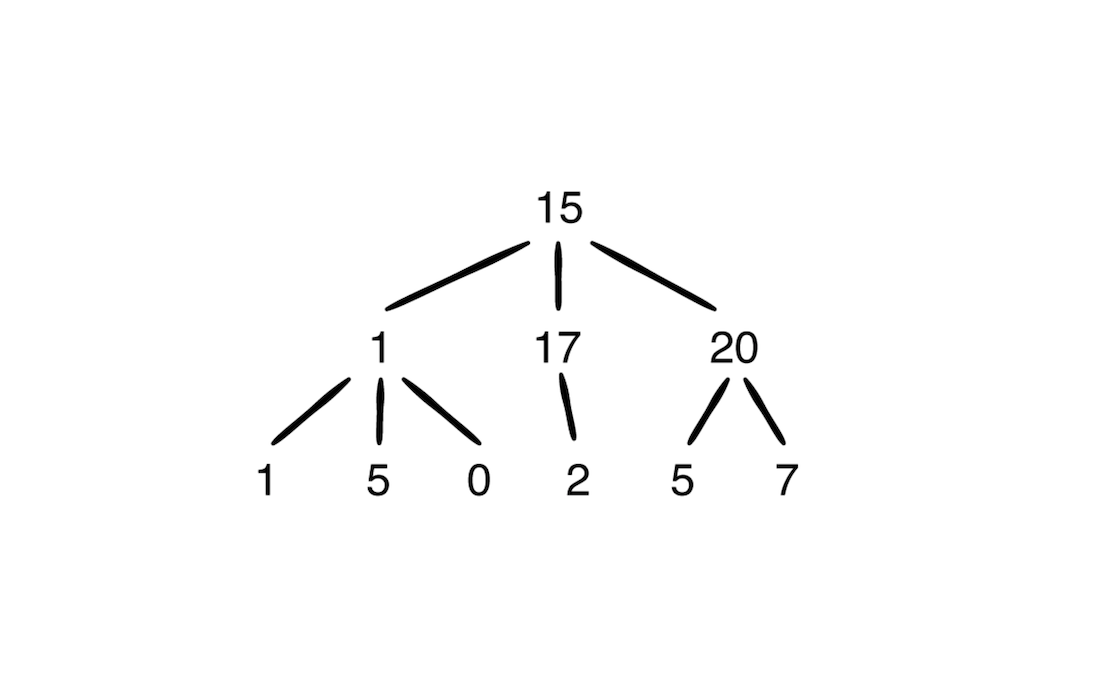
需要控制台类似输出：

15
1  17  20
1  5   0   2   5   7

一种实现方式:

    private func printEachLevel<T>(_ tree: TreeNode<T>) {
        // 创建一个队列作为数据存储
        var queue = Queue<TreeNode<T>>()
        var nodeLeftInCurrentLevel = 0
        queue.enqueue(tree)
        
        while !queue.isEmpty {
            
            // 只是记录当前出队记录的节点数目
            nodeLeftInCurrentLevel = queue.count
            
            // 出队队列当前左边节点（具体可以看队列的内部实现）
            while nodeLeftInCurrentLevel > 0 {
                guard let node = queue.dequeue() else {
                    break
                }
                
                print("\(node.value)", terminator: " ")
                // 添加到队列，但是不影响当前出队节点
                node.children.forEach { queue.enqueue($0) }
                nodeLeftInCurrentLevel -= 1
            }
            
            // 换行
            print("")
        }
    }

时间复杂度和空间复杂度都是 O(n)