定义
二叉查找树是数据结构中很常用的一种类型。首先，明确一下二叉搜索树的定义：二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。简而言之：root.left.key < root.key < root.right.key。特别地，当使用中序遍历时，可以得到一组有序的数列。
二叉查找树的插入
private static class Node {
int mData;
Node mLeft, mRight;
public Node(int value) {
mData = value;
mLeft = mRight = null;
}
}
private Node mRoot;
public BST() {
mRoot = null;
}
void insert(int target) {
mRoot = insertRec(mRoot, target);
}
Node insertRec(Node root, int target) {
if (root == null) {
root = new Node(target);
} else {
//left tree
if (target < root.mData) {
root.mLeft = insertRec(root.mLeft, target);
} else {
root.mRight = insertRec(root.mRight, target);
}
}
return root;
}
二叉树的插入大多使用递归来实现，只要满足左子树小于根，右子树大于根的特性，就很容易实现插入操作。下面，我们使用中序遍历来输出二叉树来看看效果：
void inOrder() {
inOrderRec(mRoot);
}
void inOrderRec(Node root) {
if (root != null) {
inOrderRec(root.mLeft);
System.out.print(root.mData + " ");
inOrderRec(root.mRight);
}
}
public static void main(String[] args) {
BST tree = new BST();
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
// print inorder traversal of the BST
tree.inOrder()
}
输出结果为：
20 30 40 50 60 70 80
显然，数组变得有序。因此，我们很容易联想到，二叉查找树可以用于排序。
二叉查找树的删除
二叉查找树的删除比较复杂，在展开之前，先来了解二叉查找树的几个概念。
二叉树的successor和predecessor
predecessor：前驱节点，x的predecessor满足x.key > x.predecessor.key,同时x.predecessor.key是x.key的最大下限（maximum ceiling）
successor：后继节点，x的successor满足x.key <= x.successor.key,同时x.successor.key是x.key的最小上限（minimum ceiling）
我们可以理解为，x的前驱节点是小于x的最大值，后继节点是大于x的最小值。
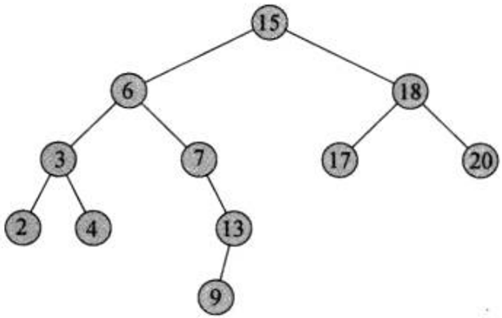前驱后继.png 如上图所示，4的前驱节点是3，后继节点是6。7的前驱节点是6，后继节点是9。
一个BST的最左叶子节点的key值就是BST所有key值中最小的。这个根据BST的特殊性质很容易推导出来：
因为 left.key < parent.key < parent.key < .... < root.key。
有了MINIMUM算法，MAXIMUM算法也就有了
Node findMinimum(Node target) {
if (target == null) {
return null;
}
//find left-most child
Node minimum = targe;
while (minimum.mLeft != null) {
minimum = minimum.mLeft;
}
return minimum;
}
Node findMaximum(Node target) {
if (target == null) {
return null;
}
//find right-most child
Node maximum = target;
while (maximum .mRight != null) {
maximum = minimum.mRight;
}
return minimum;
}
因此我们可以总结出查找前驱节点和后继节点的算法如下：
TREE-SUCCESSOR(x){
if(x.right!=null)
TREE-MINIMUM(x.right);
y=x.parent;
while(y!=null && y.left==x)
x=y;
y=y.parent;
return y;
}
TREE-PREDECESSOR(x){
if(x.left!=null)
TREE-MAXIMUM(x.left);
y=x.parent;
while(y!=null && y.right==x)
x=y;
y=y.parent;
return y;
}
理解这些概念之后，下面我们可以上删除算法了：
void deleteKey(int key) {
mRoot = deleteRec(mRoot, key);
}
/**
* A recursive function to insert a new key in BST
*/
Node deleteRec(Node root, int key) {
if (root == null) {
return null;
}
//search in left tree
if (key < root.mData) {
root.mLeft = deleteRec(root.mLeft, key);
} else if (key > root.mData) {
//search in right tree
root.mRight = deleteRec(root.mRight, key);
} else {
//find out the key,delete it
//case one: only have one child
//let root.right replace the deleted position
if (root.mLeft == null) {
return root.mRight;
} else if (root.mRight == null) {
return root.mLeft;
}
//case two: have two child
else {
//find successor（后继节点[successor]：x的后继节点是比x大的最小值；
// 前驱节点[predecessor]：x的前驱节点是比x小的最大值）
//后继节点必然在右子树，因为left<parent<right
//equals to delete [key]
root.mData = findSuccessor(root).mData;
//then,delete the successor from right tree
root.mRight = deleteRec(root.mRight, root.mData);
}
}
return root;
}
Node findSuccessor(Node target) {
if (target == null) {
return null;
}
//find left-most child
Node minimum = target.mRight;
while (minimum.mLeft != null) {
minimum = minimum.mLeft;
}
return minimum;
}
我们按照被删除的节点的子节点个数，分以下三种情况来讨论：
① 被删除节点没有孩子。只需要修改其父节点，用null去替换自己。
② 被删除节点有一个孩子。也只需要修改其父节点，用这个孩子去替换自己。
③ 被删除节点有两个孩子。那么先找z的后继y（一定在z的右子树中），并让y占据树中z的位置。z的原来的右子树部分称为y的新的右子树，并且z的左子树成为y的左子树。
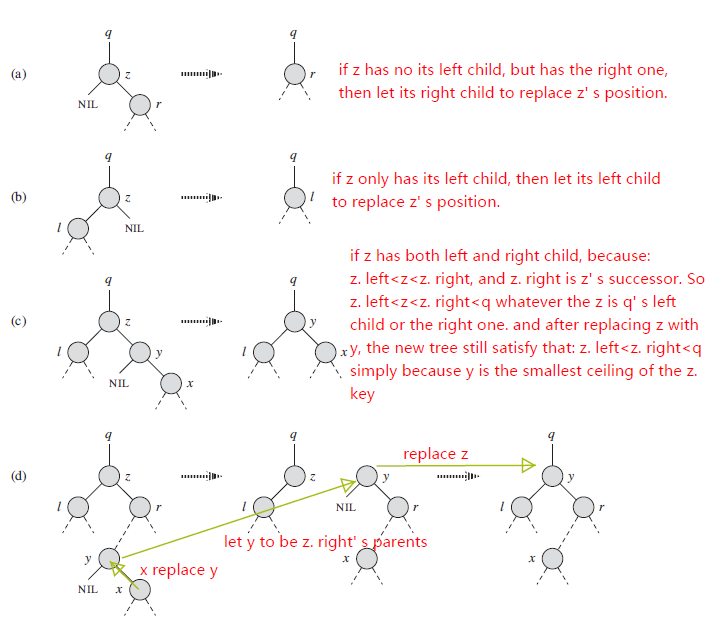删除过程
//equals to delete [key]
root.mData = findSuccessor(root).mData;
//then,delete the successor from right tree
root.mRight = deleteRec(root.mRight, root.mData);
特别需要注意，上面这两步很关键。当找到后继节点时，用后继节点替换要被删除的节点，同时需要再在右子树中递归地删除原后继节点。
最后，我们验证一下：
public static void main(String[] args) {
BST tree = new BST();
System.out.println("\nDelete 20");
tree.deleteKey(20);
System.out.println("Inorder traversal of the modified tree");
tree.inOrder();
System.out.println("\nDelete 30");
tree.deleteKey(30);
System.out.println("inOrder traversal of the modified tree");
tree.inOrder();
System.out.println("\nDelete 50");
tree.deleteKey(50);
System.out.println("inOrder traversal of the modified tree");
tree.inOrder();
}
输出结果为:
20 30 40 50 60 70 80
Delete 20
Inorder traversal of the modified tree
30 40 50 60 70 80
Delete 30
inOrder traversal of the modified tree
40 50 60 70 80
Delete 50
inOrder traversal of the modified tree
40 60 70 80
