动态规划是一种算法,通过将复杂问题分解为子问题来解决给定的复杂问题,并存储子问题的结果,以避免再次计算相同的结果。
以下是一个问题的两个主要特性,表明可以使用动态规划解决给定的问题。
- 重复子问题
- 最佳子结构
重叠子问题:
像分而治之一样,动态规划结合了子问题的解决方案。 动态规划主要用于解决一次又一次需要计算相同子问题的复杂问题。 在动态规划中,子问题的计算解决方案存储在一个表中,这样就不必重新计算。 所以当没有共同的(重叠的)子问题时,动态规划是没有用的。例如,二分搜索没有共同的子问题。 如果我们以斐波纳契数的递归程序为例,有许多子问题一次又一次地被解决。
/* simple recursive program for Fibonacci numbers */
int fib(int n)
{
if ( n <= 1 )
return n;
return fib(n-1) + fib(n-2);
}
Recursion tree for execution of fib(5)
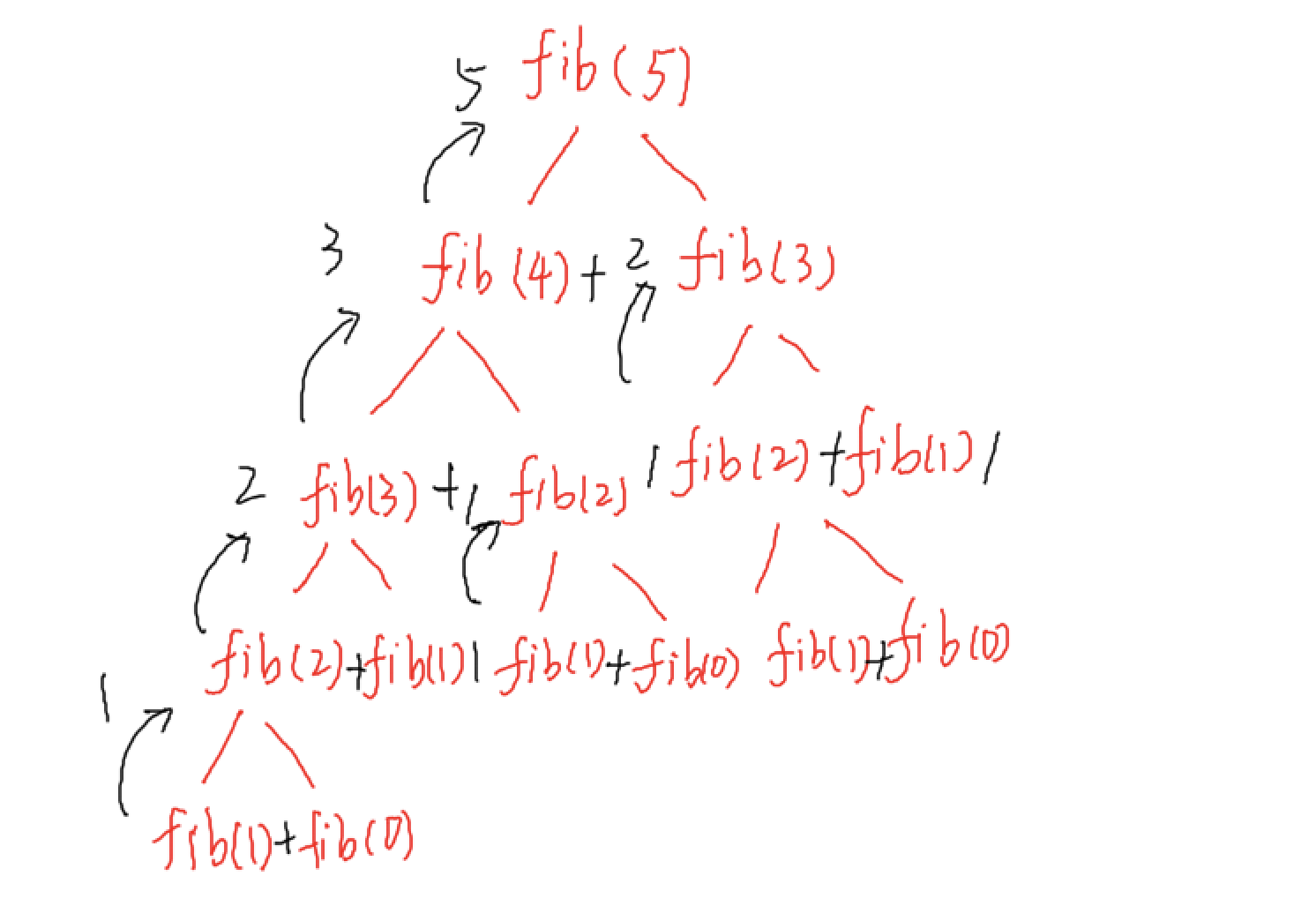
我们可以看到函数fib(3)被调用了2次。 如果我们已经存储了fib(3)的值,那么不用再次计算它,而是可以重新使用旧的存储值。 有以下两种不同的方式来存储值,以便这些值可以重复使用:
- Memoization(自上而下)
- Tabulation(自下而上)
Memoization(自上而下)
一个问题的memoized程序类似于递归版本,只是在计算解决方案之前查看一个查找表。 我们初始化一个所有初始值为NIL的查找数组。 每当我们需要解决一个子问题,我们首先查找查找表。 如果预先计算的值在那里,那么我们返回该值,否则我们计算该值并将结果放在查找表中,以便稍后可以重新使用。
以下是第n个斐波纳契数的Memoization版本。
public class Fibonacci {
final int MAX = 100;
final int NIL = -1;
int lookup[] = new int[MAX];
void _initialize() {
for (int i = 0; i < MAX; i++) {
lookup[i] = NIL;
}
}
int fib(int n) {
if (lookup[n] == NIL) {
if (n <= 1)
lookup[n] = n;
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Fibonacci f = new Fibonacci();
int n = 10;
f._initialize();
System.out.println(f.fib(n));
}
}
Tabulation(自下而上)
给定问题的表格程序以自下而上的方式构建一个表,并从表中返回最后一个条目。 例如,对于相同的斐波纳契数,我们首先计算fib(0),然后计算fib(1),然后计算fib(2),然后计算fib(3)等等。 所以从字面上看,我们正在自下而上地构建子问题的解决方案。
以下是第n个斐波纳契数字的表格版本。
public static int fib(int n) {
int f[] = new int[n + 1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
尝试以下问题作为练习。 1)为LCS(最长公共子序列)问题写一个Memoized解决方案。 请注意,Tabular解决方案在CLRS书中给出。 2)你如何选择Memoization和Tabulation?
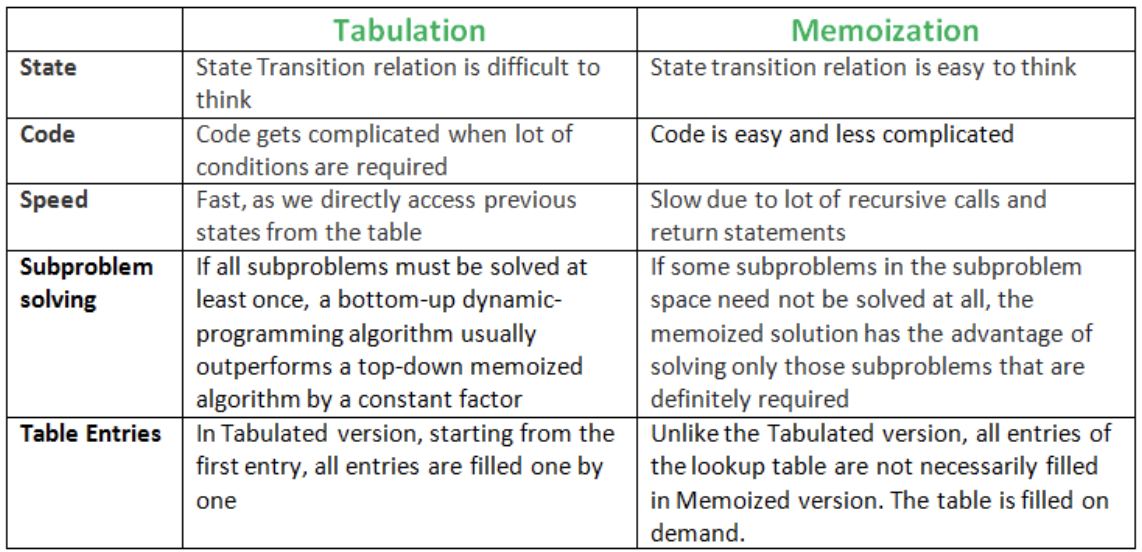
Tabulation vs Memoization

最优子结构
给定问题具有最优子结构性质,如果给定问题的最优解可以通过使用子问题的最优解得到。 例如,最短路径问题具有以下最佳的子结构属性:如果节点x位于从源节点u到目的节点v的最短路径,那么从u到v的最短路径是从u到x的最短路径和从x到v的最短路径的组合。标准的 All Pair Shortest Path算法如Floyd-Warshall和Bellman-Ford都是动态规划的典型例子。 最长路径问题没有最佳子结构属性。
如何解决动态规划问题
步骤: 确定是否为dp问题--->用最少的参数决定一个状态表达式--->确定不同状态之间的关系--->使用tabulation或memoization
dp问题一般都会包含一个状态,即子问题,而子状态之间如何转换就是一个关键。 什么是状态呢?一个状态可以被定义为一组参数,它可以唯一地标识某个特定的位置或站在给定的问题中。 这组参数应尽可能小以减少状态空间。
例如:在我们着名的背包问题中,我们用两个参数index和weight定义我们的状态,即DP [index] [weight]。 在这里DP [指数] [权重]告诉我们,通过从范围0到指数具有袋装能力的物品可以获得的最大利润是重量。 因此,这里的参数指标和权重可以唯一地识别背包问题的子问题。
所以,我们的第一步就是在确定问题是DP问题之后,再为问题决定一个状态。
因为我们知道DP是用计算结果来制定最终结果的。所以,我们下一步将要找到之前的状态和目前的状态之间的关系。 这部分是解决DP问题的最难的部分,需要大量的观察和练习。 让我们通过考虑一个示例问题来理解它
给定3个数字{1,3,5},我们需要告诉 我们可以组成一个数字“N”的总数, 使用给定的三个数字的总和。 (允许重复和不同的安排)。
形成6的方法总数是:8
1 + 1 +1 + 1 +1 + 1
1 + 1 +1 + 3
1 + 1 +3 + 1
1 + 3+ 1 + 1
3 + 1+ 1 + 1
3 + 3
1 + 5
5 + 1
dp[n]表示通过使用{1,3,5}作为元素来形成n的排列的总数。 假设我们已经知道了dp[1],dp[2],dp[3]...,dp[6]。而我们希望算dp[7]。 dp[7] = dp[7 - 1] + dp[7 - 3] + dp[7 - 5] dp[7] = dp[6] + dp[4] + dp[2] 故dp[n] = dp[n-1] + dp[n - 3] + dp[n - 5]
int solve(int n){
if(n < 0)
return 0;
if(n == 0)
return 1;
return solve(n-1) + sovle(n-3) + solve(n-5);
}
Adding memoization or tabulation for the state
// initialize to -1
int dp[MAXN];
// this function returns the number of
// arrangements to form 'n'
int solve(int n)
{
// base case
if (n < 0)
return 0;
if (n == 0)
return 1;
// checking if already calculated
if (dp[n]!=-1)
return dp[n];
// storing the result and returning
return dp[n] = solve(n-1) + solve(n-3) + solve(n-5);
}
Tabulation vs Memoizatation
Tabulation Method – Bottom Up Dynamic Programming
正如名字本身所暗示的,从底部开始,积累到顶部的答案。 让我们从状态转换的角度来讨论。 让我们将DP问题的状态描述为dp[x],其中dp[0]为基态,dp[n]为目标状态。 所以,我们需要找到目标状态的值,即dp[n]。 如果我们从基态dp[0]开始转换并且跟随我们的状态转换关系到达我们的目标状态dp[n],我们称之为自下而上方法,因为我们很清楚地开始了从最底部 状态并达到最理想状态。
Memoization Method – Top Down Dynamic Programming
我们从最高的目标状态开始,并通过计算可以达到目的地状态的状态的值来计算它的答案,直到我们达到最底层的基本状态。
使用动态规划解决背包问题
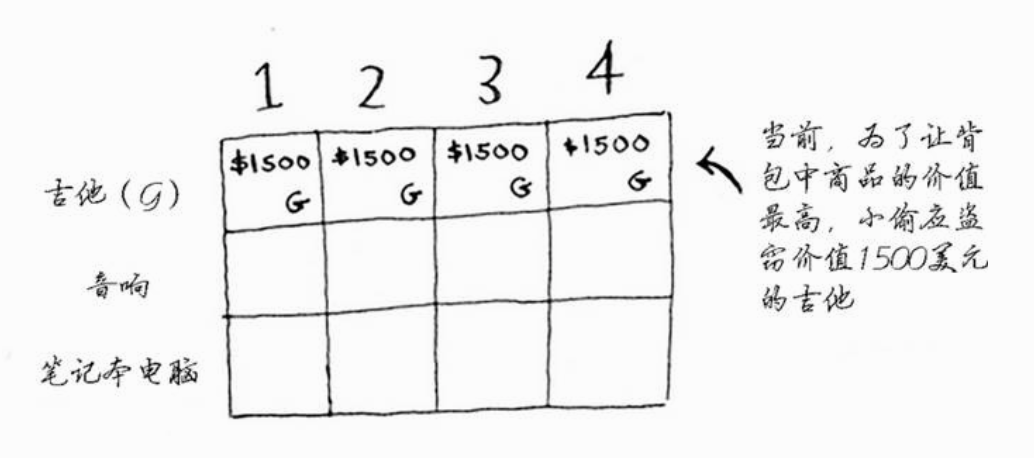
每个动态规划算法都从一个网格开始,背包问题的网格如下:
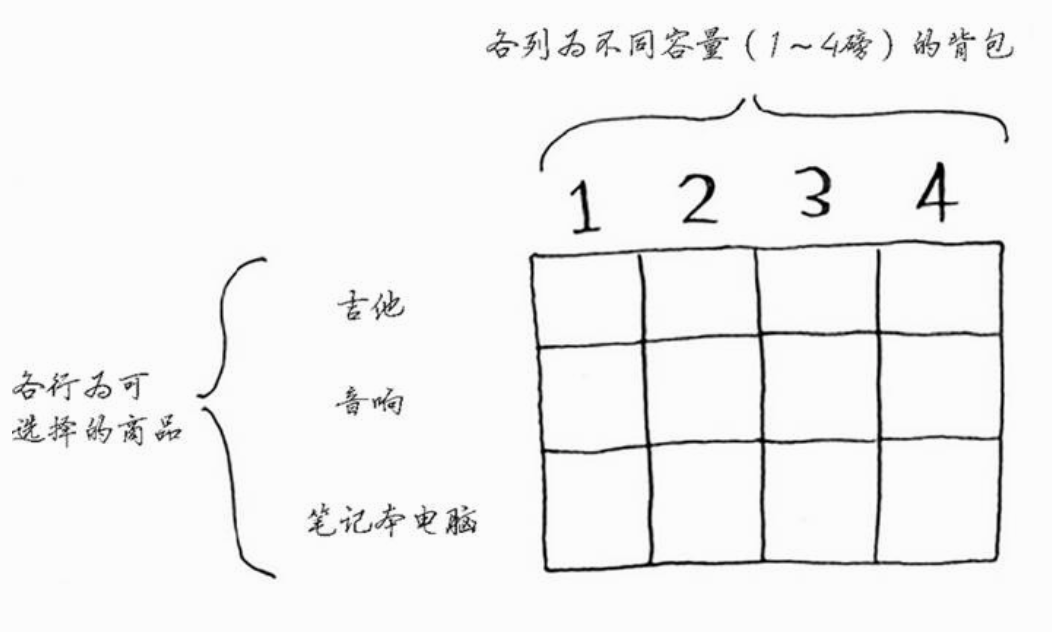
其中吉他价值1500,占容量1,笔记本电脑价值2000,占容量3,音响价值3000,占容量4。
网格的各行为商品,各列为不同容量(1~4磅)的背包。
- 吉他行
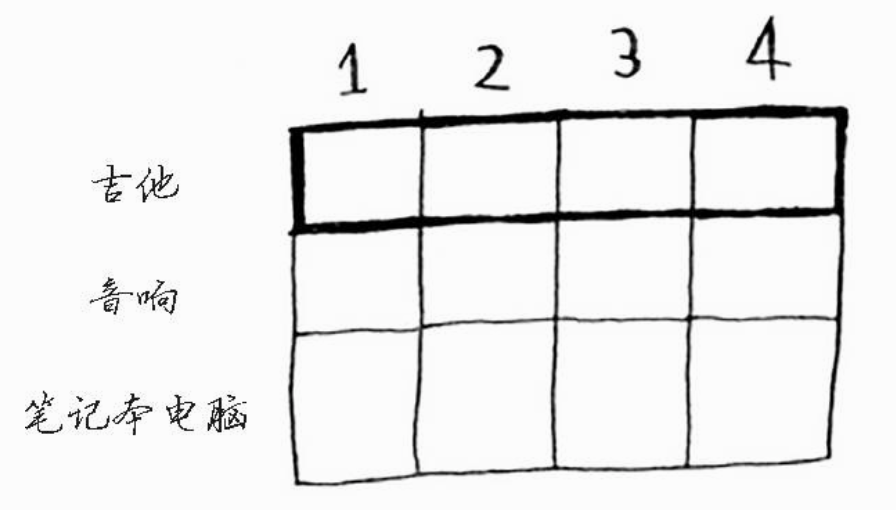
第一个单元格表示背包的容量为1磅。吉他的重量也是1磅,这意味着它能装入背包!因此这个单元格包含吉他,价值为1500美元。
-
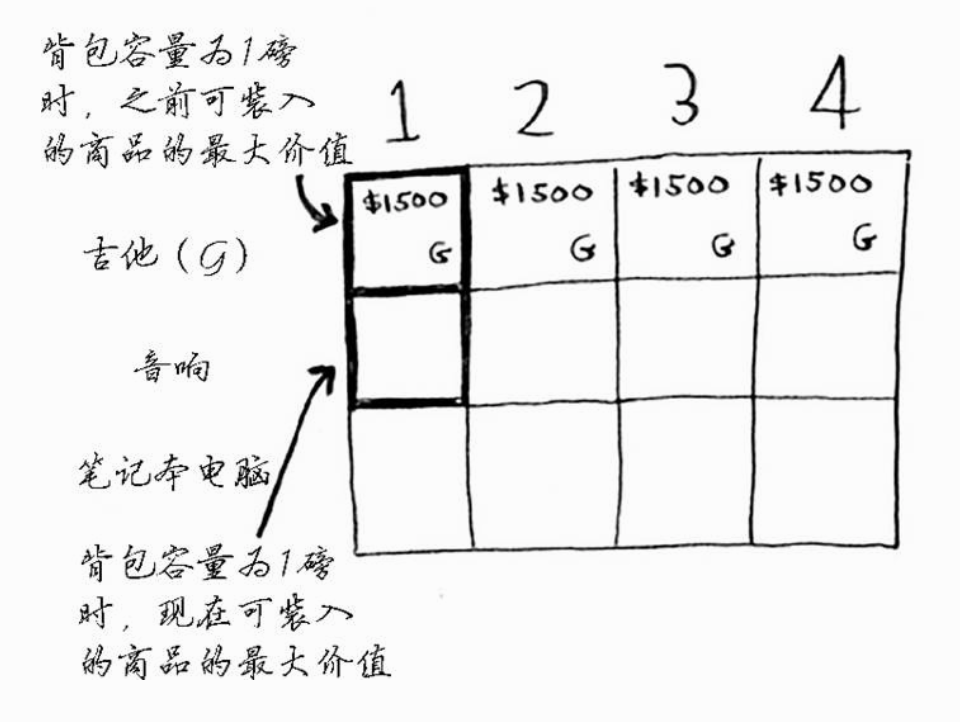
音响行
你现在出于第二行,可偷的商品有吉他和音响。在每一行,可偷的商品都为当前行的商品以及之前各行的商品
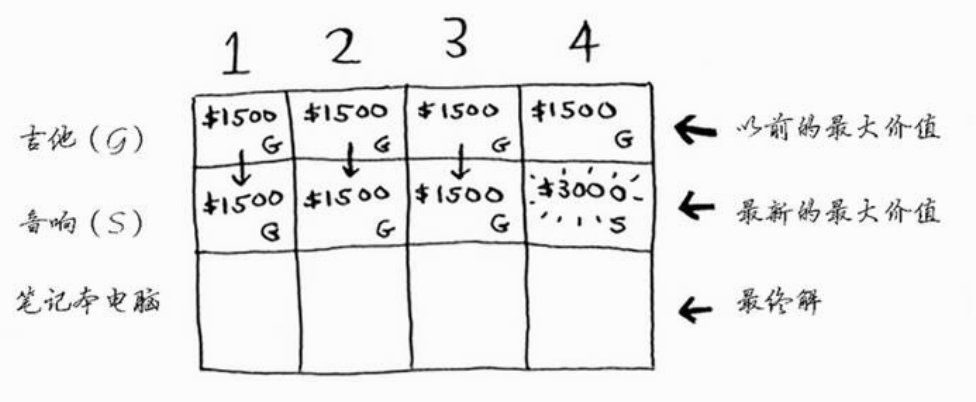
- 笔记本行

计算每个单元格的价值时,使用的公式都相同。这个公式如下。
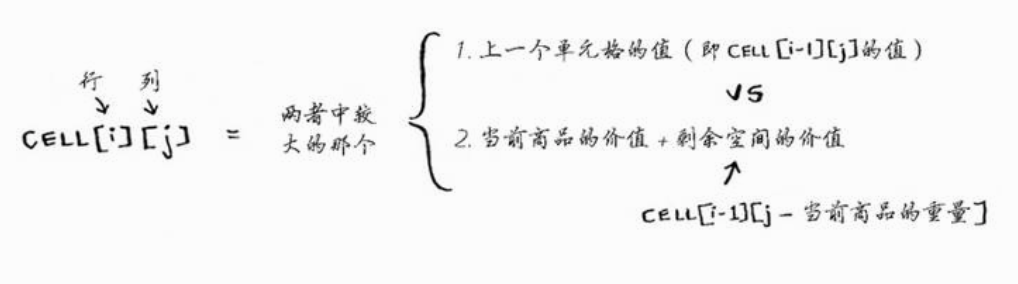
背包问题实现代码:
BagObject类,表示装入背包中的物件
public class BagObject {
public int capaticy;
public int value;
public BagObject(int cap, int val) {
// TODO Auto-generated constructor stub
this.capaticy = cap;
this.value = val;
}
}
public class PackageProblem {
private int cap;
private BagObject[] objs;
private int[][] dp;
public PackageProblem(int bagCap, BagObject[] objs) {
// TODO Auto-generated constructor stub
cap = bagCap;
this.objs = objs;
dp = new int[this.objs.length][cap];
}
public int getMaxValue() {
int nowval = objs[0].value;
int nowcap = objs[0].capaticy;
int i, j;
for (i = 0; i < cap; i++) {
if (i + 1 >= nowcap && dp[0][i] < nowval) {
dp[0][i] = nowval;
}
}
for (i = 1; i < this.objs.length; i++) {
nowcap = objs[i].capaticy;
nowval = objs[i].value;
for (j = 0; j < cap; j++) {
if (j + 1 - nowcap > 0) {
dp[i][j] = Math.max(dp[i - 1][j], nowval + dp[i - 1][j + 1 - nowcap]);
} else {
dp[i][j] = Math.max(dp[i - 1][j], nowval);
}
}
}
return dp[objs.length - 1][cap - 1];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
BagObject guiter = new BagObject(1, 1500);
BagObject tap = new BagObject(3, 2000);
BagObject radio = new BagObject(4, 3000);
BagObject[] objs = new BagObject[3];
objs[1] = guiter;
objs[0] = tap;
objs[2] = radio;
PackageProblem pp = new PackageProblem(4, objs);
System.out.println(pp.getMaxValue());
}
}
使用动态规划解决LCS问题
-
绘制表格
考虑三个问题:单元格中的值是什么?如何将这个问题划分为子问题?网格的坐标轴是什么?
单元格中的值通常就是你要优化的值。在这个例子中为:
两个字符串都包含的最长子串的长度。假设比较fish和hish。
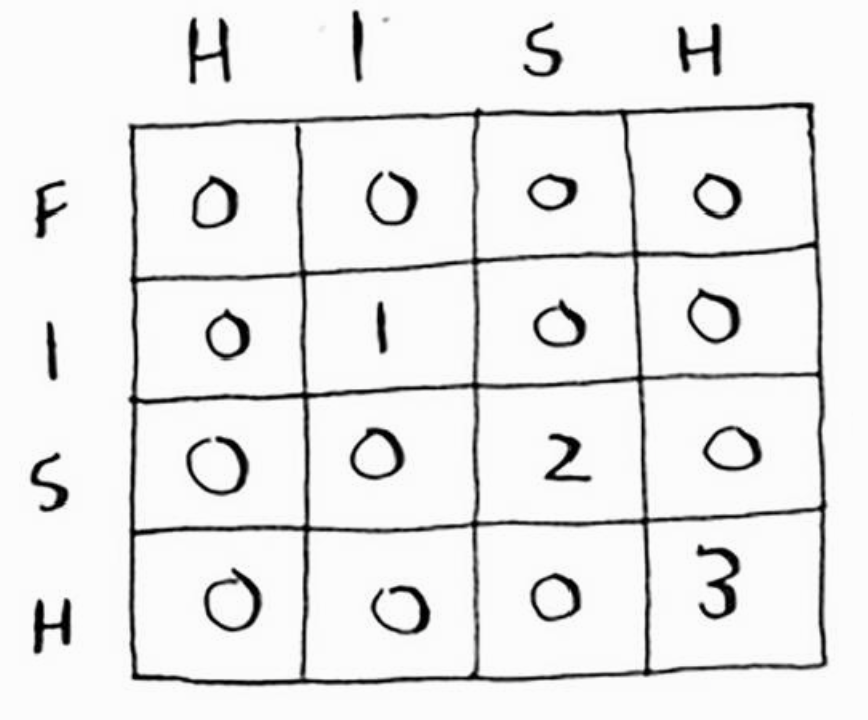
- 公式


答案为网格中最大的数字。
最长公共子序列
两个单词中都有的序列包含的字母数
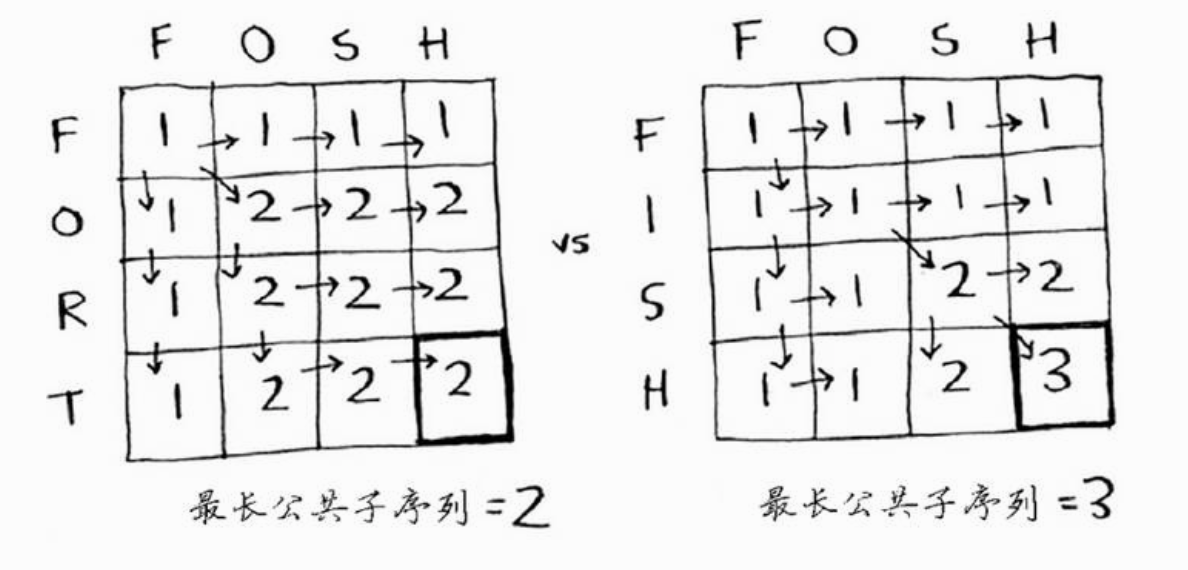
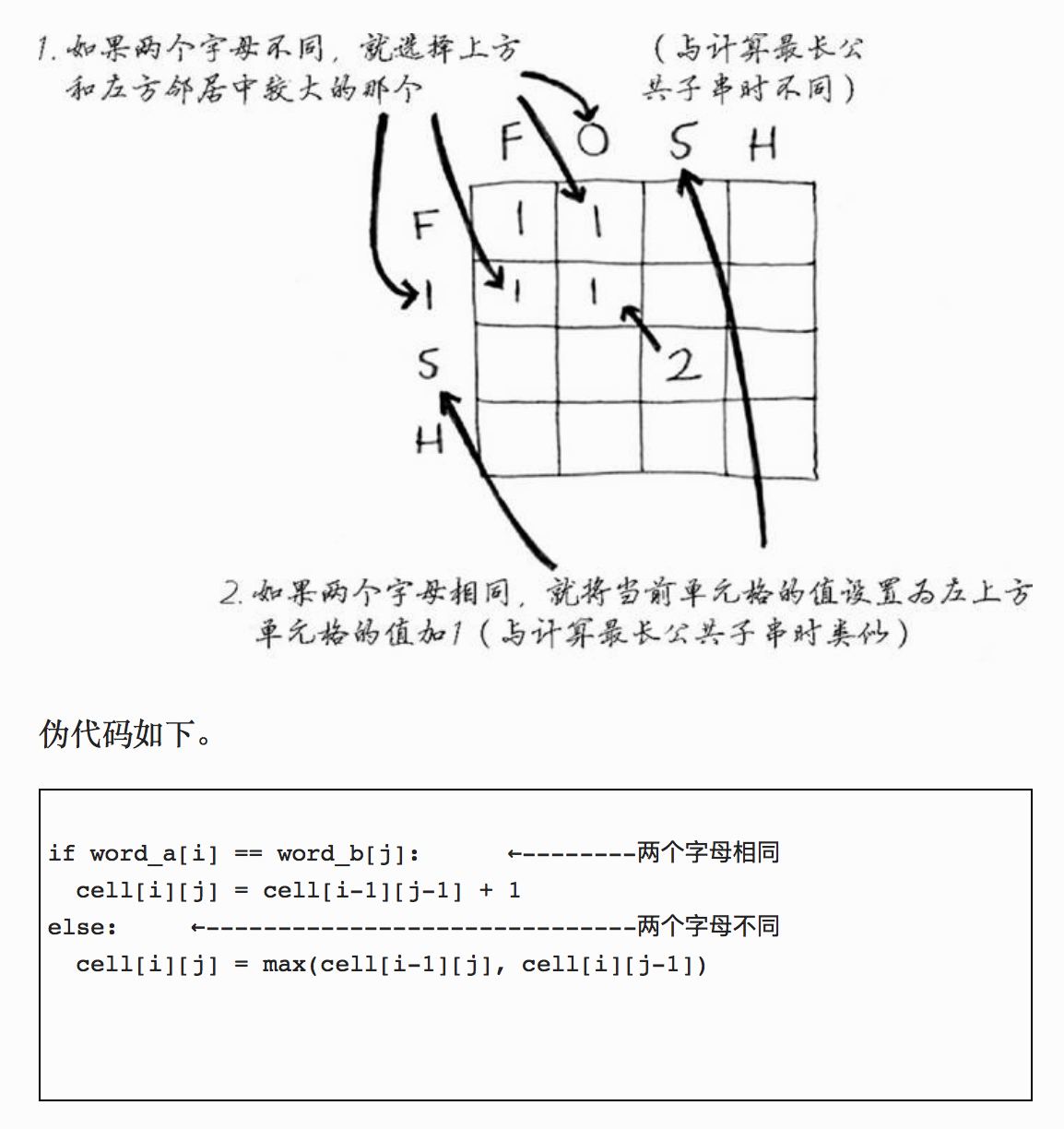
实现代码
public class LongCS {
public static int lcs(String a, String b) {
int[][] dp = new int[a.length() + 1][b.length() + 1];
for (int i = 1; i < a.length() + 1; i++) {
for (int j = 1; j < b.length() + 1; j++) {
if (a.charAt(i - 1) == b.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[a.length()][b.length()];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println(lcs("AGGTAB", "GXTXAYB"));
}
}