1.从一道面试题开始
每个程序员从第一次接触计算机编程语言到真正作为工程师进行项目开发,都一定都见过下面这道题目:
- 很多个台阶,可以一次走一个台阶,也可以一次走两个台阶,那么走台阶时,有多少种可能?
解法有很多种,最经典的当属递归解法,围绕此解法的核心思想正是大名鼎鼎的斐波那契数列。(递归解法虽然计算量很大,但算法优化相关内容不本是文讨论范围)。
2.斐波那契是谁
斐波那契(Leonardo Fibonacci)是意大利数学家,主要研究方向为几何学,三角学,多元方程解法,在1202年发表了《算盘全书》,他英俊的面庞见下图:

3.斐波那契数列
什么是斐波那契数列?
简单来说,就是有这样一个数列,它的每一项都是前两项之和。那么从零开始的数列是这样的:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
3.1 斐波那契数列的通项公式
如果设为该数列的第n项(n∈N*),则有(请注意n为正整数,下文默认该范围):
这似乎与我们印象中的什么n-1和n-2的解法不太一样,这是因为上述式叫做数列的通项公式。在斐波那契数列中有两个公式,对应的中文名称如下:
- 斐波那契数列通项公式
- 斐波那契数列表达式
这样看来,我们平时用编程语言编写的递归方法,其实就是斐波那契数列表达式,而表达式是可以推导出通项公式的,这也是本文的重点。在进行推导之前我们先补充一些基本的数列知识。
4.数列基础知识
数学中的数列分为很多种,其中一种就是递推数列,意思就是数列的每一项都可以通过其他项推理出来。与方程的一元二元等定义类似,递推数列也存在类似“元”的概念,称之为“阶”。而斐波那契数列就是二阶递推数列。我们先来看下递推数列的相关定义:
定义:数列的每一项由前一项或前几项的函数决定,是谓递推数列
通项公式:
,其中
k称为递推数列的阶
当我们令k=2时,上述通项公式变为:
恰好符合斐波那契数列每一项由前两项决定的特性,由此也可以推出,斐波那契数列是二阶递推数列的充分不必要条件。
5.斐波那契数列通项公式的推导
如何通过数列表达式推导出数列的通项公式?
在推导之前,我们可以回想一下高中数学课上,是如何推导二元一次函数方程式的?常用的方法就是设:
同样的道理,求数列的通项公式也可以简化成:
我们只要设法求得f(n)是什么就可以了。思路确定之后,可以开始探索解法了。
假设有(记为1式):
进行第一次变形(记为2式):
变形到这里了,那么下一步该怎么办呢?此处需要灵活发散的联想,否则真的很难继续前行。我们观察到,等号右侧的两式的参数恰好就是二元一次方程组的解的通项公式啊!于是令:
而根据二次方程根与系数关系,和
恰好是方程
的解。又因为我们知道
,由此可推出之后每一项的值,故代入1式中可求得a,b,c的值(记为3式):
由2式可得:
我们回到2式,进行第二次变形得:
打开括号,第三次变形得(记为3式):
等号两边同时除,得:
这样我们又回到了高中的数学课堂,因为我们观察发现,这是一个等比数列:
是一个等比数列,公比为
同理在3式中,如果我们把移到左边,可以得到:
是一个等比数列,公比为
由等比数列通项公式得(记为4式):
同理可得(记为5式):
4式和5式相减,可得:
由此我们由数列的表达式推导出了数列的通项公式:
6.斐波那契数列与黄金分割比
直接给结论:斐波那契数列相邻项比值的极限是0.618。
意思就是随着斐波那契数列越来越大,相邻两项的比值越来越接近0.618。证明也非常简单,只要有大学高数的极限知识即可:
假设极限存在,那么设极限为Q
7.斐波那契数列的应用
自然界中存在大量的斐波那契数列案例,人们也将斐波那契数列广泛应用在工业,建筑等等方面,相信大家都已经耳熟能详了,本文也不再赘述。不过在此有必要介绍一个有趣的玩具,叫做斐波那契钟:
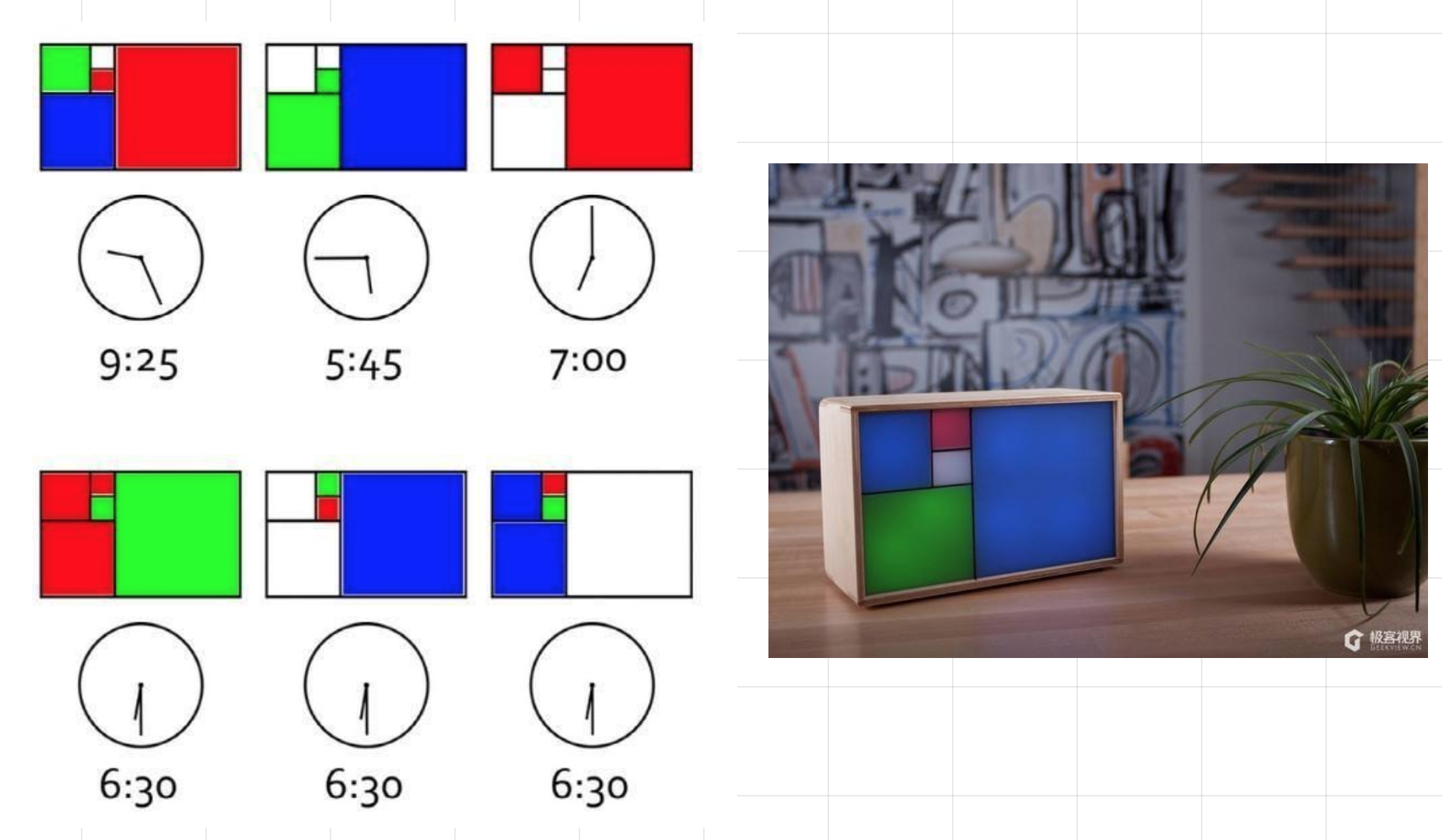
如何计算当前时间呢?
钟面上是5个正方形方块,大小有不同,每个方块的边长对应的分别是斐波那契序列的1,1,2,3,5,它们代表的是小时或分钟的数值,那么则有:
小时数 = 红色数值 + 蓝色数值
分钟数 = (绿色数值 + 蓝色数值) x 5
笔者觉得此钟逼格满满,但是谁用遭罪,试想一下早起睡眼朦胧的时候还要心算时间,哈哈哈~
8.斐波那契数列的拓展
8.1 反斐波那契数列
该数列的相邻项比值为-0.618,与斐波那契数列的相邻项比值恰好相反。
8.2 巴都万数列
巴都万数列的表达式如下:
巴都万数列有什么特点呢?斐波那契数列可以用正方形来描述:
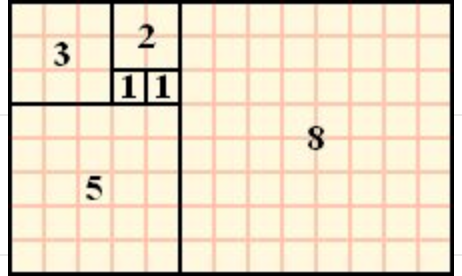
而巴都万数列可以用三角形来描述:
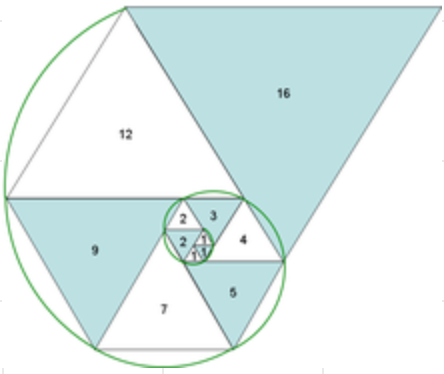
数学真奇妙~~
9.总结
斐波那契数列作为程序员最早接触也是最简单的数学逻辑,不但可以用基础的高中数学知识进行推理,而且具有丰富的趣味性,令人不禁赞叹数学之美。